相信大家都听说过股票和债券的多元化投资组合。
最近我们被客户要求撰写关于股票交易策略的研究报告。改进的股票配对交易策略基本上使用了一种前进的方法，即最大化夏普比率，偏向于波动率而不是收益率。
视频
量化交易陷阱和R语言改进股票配对交易策略分析中国股市投资组合
也就是说，它使用72天的移动窗口来最大化投资组合的不同权重配置之间的总收益，标准差提高到52的幂。
股票配对交易是统计套利的主要内容之一，它旨在寻找市场上历史走势相似的股票进行配对，当价格差较大（高于历史均值）时高卖低买进行套利。统计套利虽然增加了一些风险，但也伴随着诱人的风险溢价，即获得更多套利机会；不过其本质上的局限性也是非常明显，基于历史数据，其只能反映过去的信息，用之预测未来有时难以讲得通。下面简单阐述下股票配对交易的几种方法：
一.距离法
距离法是使用一个回溯时间区间，标准化价格。然后在 2 范数下计算 n 只股票两两间的配对距离（SSD）。以 SSD 值最小的前 20 对作为标的，在后续 6 个月内以 2 倍标准差作为阈值进行统计套利，距离回到均值时平仓。6 个月后更新标的继续套利。
此方法的标的选择标准中蕴含着其无法最大化利润，因每对的收益与其价差（SSD）成正比；此外高相关性不代表协整，从而均值回复得不到保证。
二.协整法
该方法的前提是不平稳的经济时间序列的线性组合可能实现平稳。
用对数价格进行OLS 回归，对残差进行 ADF 检验，其中误差修正模型为 Johansen 方法。若验证了协整关系，即可说明股价 A,B之间存在长期均衡关系，从而残差序列是均值回复的。
此方法模型太单一，标的仅为两种股票，时限仅限于 2 年之内，单笔收益最大化不保证整体收益最大化。
三.时间序列法
时间序列法是假定价差为具有均值回归特性的马尔科夫链，伴随着高斯噪声。
该方法优越性在于抓住了配对交易的核心—均值回复性；其次该模型是连续的，因而可以用于预测；最后，该模型易处理，可通过卡尔曼滤波方法得到最小 MSE 参数估计。不过，价差应使用价格的自然对数差来避免量纲不同的影响；模型条件苛求收益平价，这实际很难达到；金融资产数据现实中并不满足Ornstein-Uhlenbeck 过程。
说得通俗一点，在1的幂数下，这是基本的夏普比率，在0的幂数下，只是一个动量最大化的算法。
这个策略的过程很简单:每个月重新平衡SPY和TLT之间5%的倍数，之前最大化了以下数量(在72天窗口中返回波动率^2.5)。
SPY和TLT组合
以下是获取数据和计算必要数据的代码:
require(quantmod)
getSymbols(c("SPY", "TLT"), from="1990-01-01")
for(i in 1:21)
weightSPY <- (i-1)*.05
config <- Return.portfolio(R = returns, weights=c(weightSPY, weightTLT)
period <- 72 接下来，建立权重的代码：
weights <- t(apply(monthlyModSharpe, 1, findMax))
weights[is.na(weights)] <- 0 也就是说，在每个重新平衡的日期(每月的月末)，简单地采用使每月修改的夏普比率计算最大化的设置。接下来是收益表现:
Performance(stratRets)结果如下:
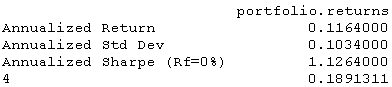
具有以下股票曲线：
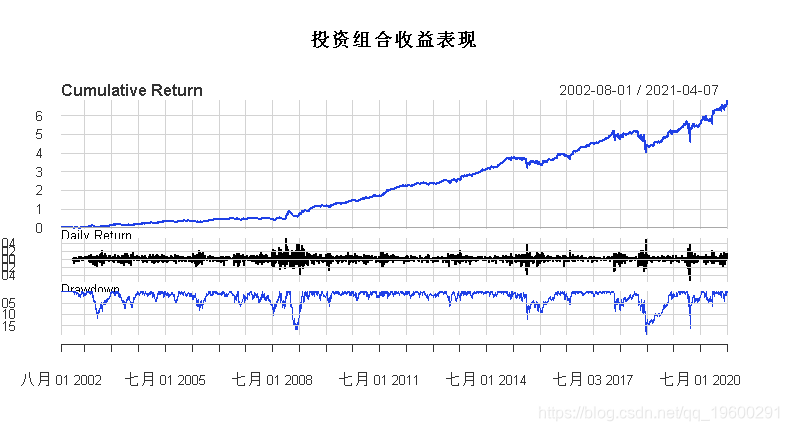
并不完美，但相比之下，它的成分如何呢，我们来看看。
apply.yearly(Components, Return.cumulative)以下是一些常见的统计数据:
简而言之，这一策略的表现似乎远远好于上述两种成分。我们来看看股票曲线的比较是否反映了这一点。
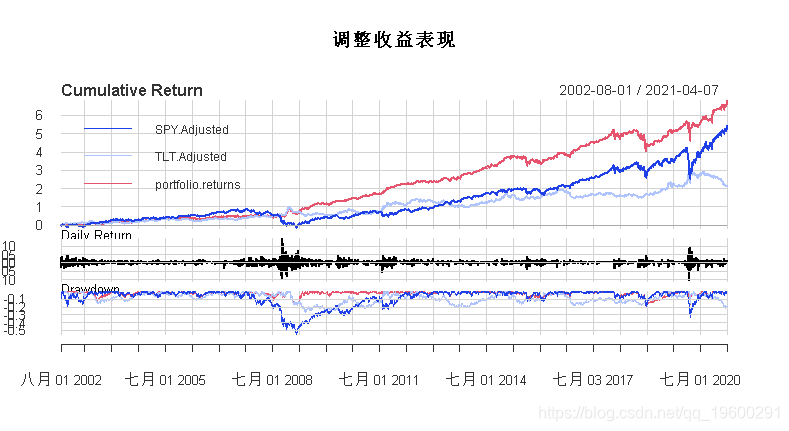
事实上，虽然它确实在危机中出现了下跌，但当时这两个工具都在下跌，所以看起来这个策略在糟糕的情况下取得了最好的效果.以下是年度收益。
随时关注您喜欢的主题
yearly(Return.cumulative) 
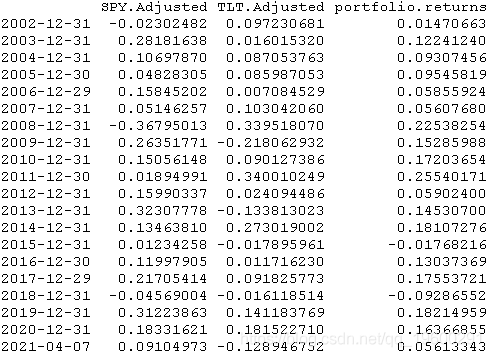
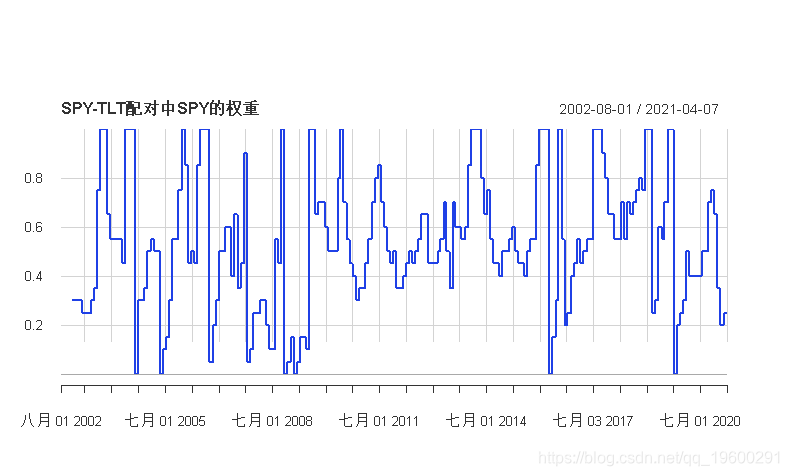
然而，从2002年整体上看，虽然该策略很少会像两个中更好的表现一样，但它总是比两个中更差的表现出色–不仅如此，即使在一个表现差的时候，该策略在回测的每一年中都取得了积极的表现，例如2008年的SPY，以及2009年和2013年的TLT。以下是SPY在策略中的权重。
weightSPY <- do.call(rbind, weightSPY)
TimeSeries(alig, date.format="%Y", ylab="SPY权重", main="SPY-TLT配对中SPY的权重")
贵州茅台和民生银行组合
股票数据获取及整理
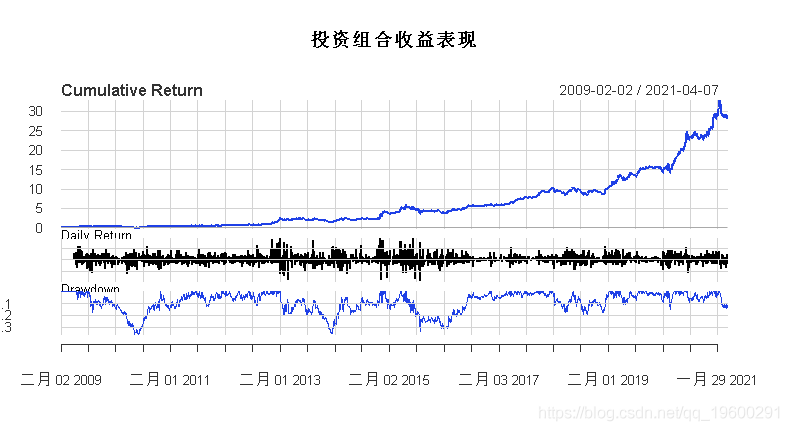
## [1] "GZMT" "MSYH"组合收益表现结果如下:
加入比较项-非组合下的单只表现
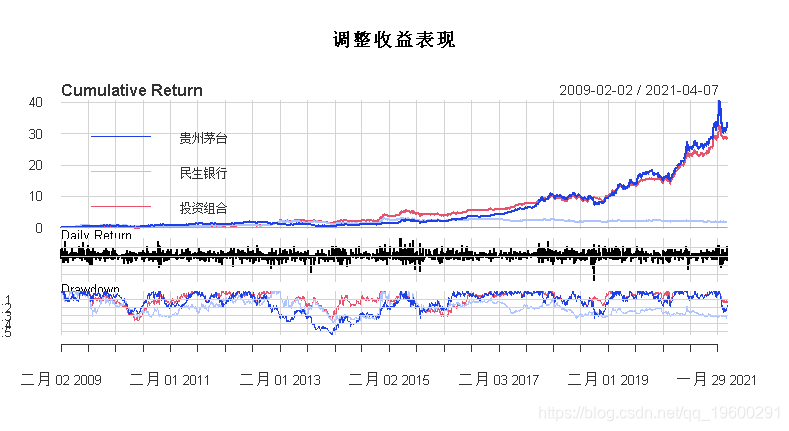
通过累积收益率、日收益率和最大回撤率，以及年化收益率比较，可以发现采用优化方法的投资组合明显优于传统的投资策略。
年化收益率比较
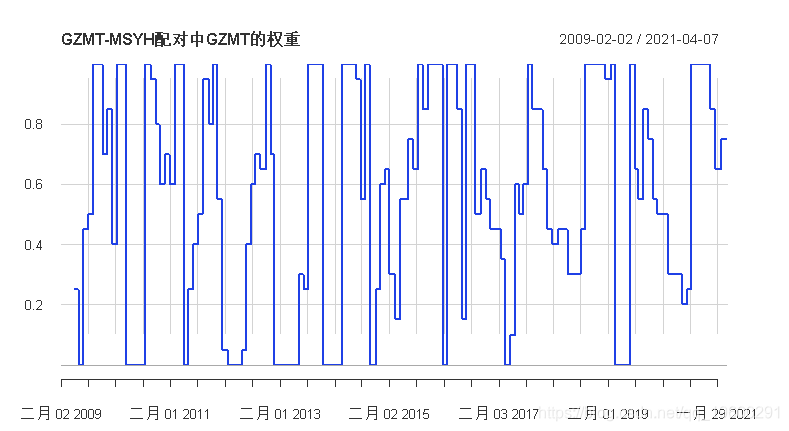
现在，虽然这对某些人来说可能是一个独立的策略，但在我看来，动态地重新加权两个具有负相关性的收益流，与它们形成的成分相比，可能会产生一些较好的结果。此外，模拟实际组合收益率所采用的方法很有趣，不是简单地依靠一个数字来总结两种工具之间的关系，毫无疑问，这种方法作为一种一般的前进方法，有着广泛的应用。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python生成对抗神经网络GAN预测股票及LSTMs、ARIMA对比分析ETF金融时间序列可视化
Python深度强化学习对冲策略：衍生品投资组合套期保值Black-Scholes、Heston模型分析
Python深度强化学习智能体DDPG自适应股票交易策略优化道琼斯30股票数据可视化研究
