
通过对用电负荷的消费者进行聚类,我们可以提取典型的负荷曲线,提高后续用电量预测的准确性
第一个用例通过K-medoids聚类方法提取典型的电力负荷曲线。
可下载资源
有50个长度为672的时间序列(消费者),长度为2周的耗电量的时间序列。这些测量数据来自智能电表。
GAM是由数据驱动而非统计分布模型驱动的非参数回归模型,可对部分解释变量进行线性拟合,对其他因子进行光滑函数拟合。模型不需要预先设定参数模型,模型通过解释变量的平滑函数建立,能够自动选择合适的多项式。GAM属于非参数回归模型中的一种,非参数回归不需要模型满足线性的假设前提,可以灵活的探测数据间的复杂关系。并且利用机器学习方法的输入并没有考虑到影响因子之间的交互作用,为了考虑影响因子之间的交互作用。
GAM,属于半参模型中的一种,其表示形式如下所示:
g(u)=a+f1(X1)+f2(X2)+⋯+fp(Xp)
其中, u=E(Y/X1,X2,X3,⋯,Xp),g(u) 是连接函数, f1,f2,⋯,fp 是连接解释变量的平滑函数,Xi为解释变量,fi(Xi)是关于Xi的非指定类别的非参数函数。
在该模型中,响应变量的分布可以是正态分布,二项分布、poisson分布等。对fi(Xi)的估计方法有平滑样条法,局部加权回归散点平滑法、薄板平滑样条法,平滑参数的选择有交叉验证法、广义交叉验证法等。
像线性回归一样,可以通过增加形式为Xi × Xj的交互项,使得GAM能够体现交互效应的作用。另外,可以增加形式为fu(Xi, Xj)的低维交互项,这样的交互项可以应用一些二维光滑方法,如局部回归或者二维样条来拟合。
GAM应用的潜在假设为函数是可加的,允许每个协变量作为一个不加限制的平滑函数,而不是仅仅作为一种呆板的参数函数被拟合,对部分或全部的解释变量采用平滑函数的方法建立模型。GAM与GLM共同的特点是用连接函数来估计响应变量和各解释变量间的关系。与GLM不同的是GAM中的各函数可以是非参数的形式,因而使得其应用范围更为广泛,GAM是GLM的一种推广。因此GAM适用于多种分布类型,多种复杂非线性关系的分析。
对于用电的两个季节性时间序列(每日和每周季节性),基于模型的表示方法是提取典型用电量的最佳方法。
视频
R语言广义相加模型(GAM)在电力负荷预测中的应用
视频
KMEANS均值聚类和层次聚类:R语言分析生活幸福质量系数可视化实例
让我们使用一种基于模型的基本表示方法- 平均季节性。在此还有一个非常重要的注意事项,对时间序列进行归一化是对时间序列进行每次聚类或分类之前的必要步骤。我们想要提取典型的消耗曲线,而不是根据消耗量进行聚类。
维数上已大大降低。现在,让我们使用K-medoids聚类方法来提取典型的消耗量。由于我们不知道要选择合适的簇数,即先验信息,因此必须使用验证指数来确定最佳簇数。我将使用Davies-Bouldin指数进行评估。通过Davies-Bouldin指数计算,我们希望找到其最小值。
我将聚类数的范围设置为2-7。
让我们绘制评估的结果。
ggplot(data.table(Clusters = 2:7, DBindex = unlist(DB_values)),
aes(Clusters, DBindex)) +
geom_line(size = 1) +
geom_point(size = 3) +
theme_bw()
聚类的“最佳”数目是7。
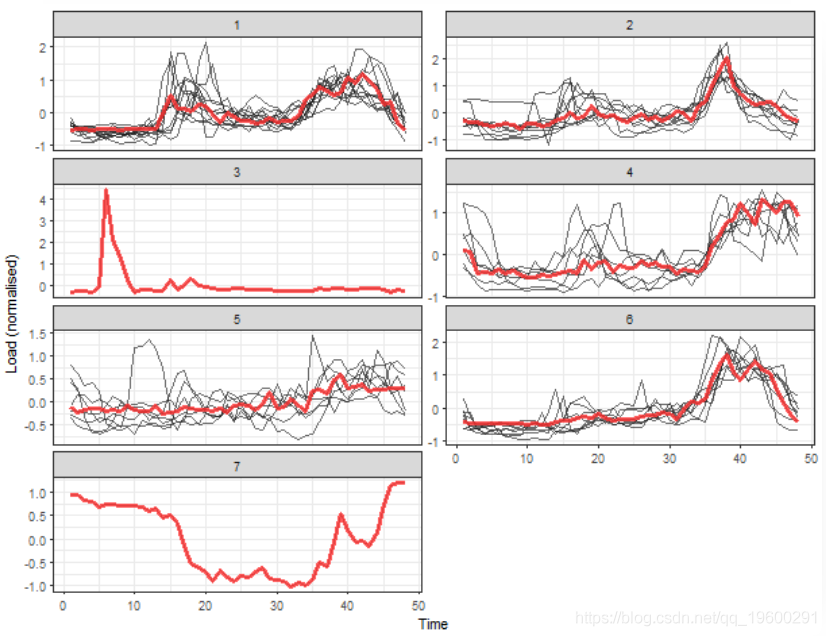
我们绘制有7个聚类的聚类结果。
我们可以看到5个典型的提取轮廓 (簇的中心)。接下来的两个簇可以称为离群值。
现在,让我们尝试一些更复杂的方法来提取季节 GAM回归系数。 我们可以提取每日和每周的季节性回归系数 。
## [1] 50 53由于GAM方法中使用样条曲线 。让我们对数据进行聚类并可视化其结果。
让我们绘制 评估的结果。
ggplot(data.table(Clusters = 2:7, DBindex = unlist(DB_values)),
aes(Clusters, DBindex)) +
geom_line(size = 1) +
geom_point(size = 3) +
theme_bw()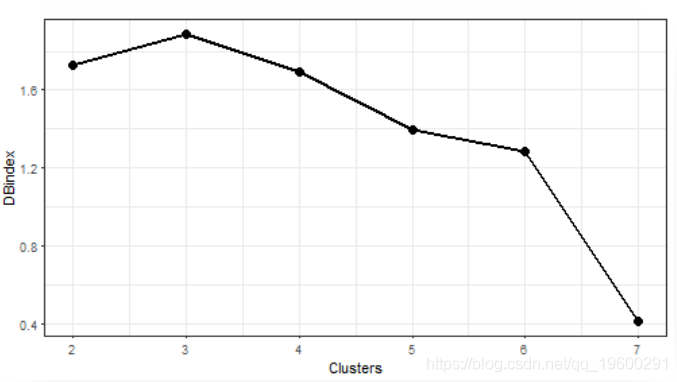
聚类的最佳数目为7。让我们绘制结果。
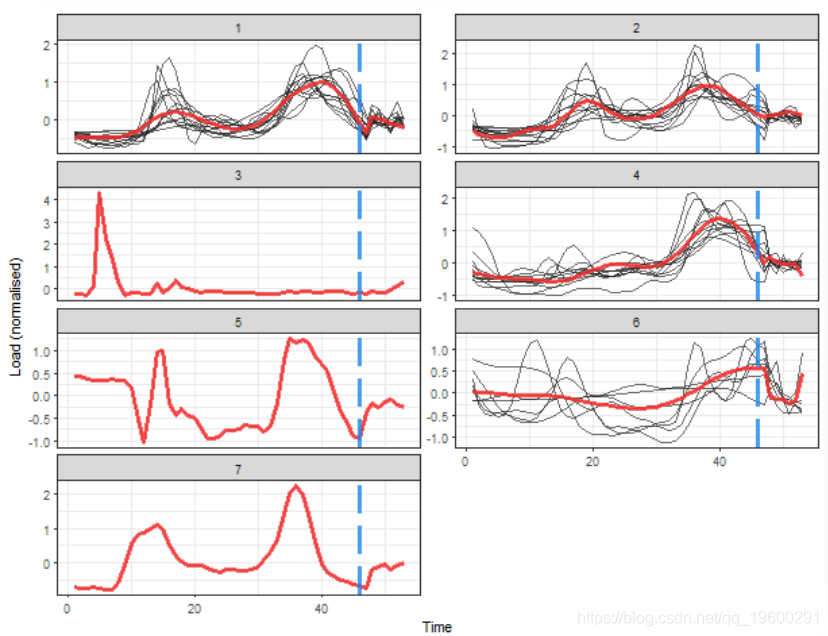
提取的消费数据比平均季节性数据更平滑。 现在,K 中心提取了4个典型的轮廓,并确定了3个簇。
我展示自适应表示的聚类结果,我们以DFT(离散傅立叶变换)方法为例,并提取前48个DFT系数。
dim(data_dft)## [1] 50 48让我们绘制评估的结果。
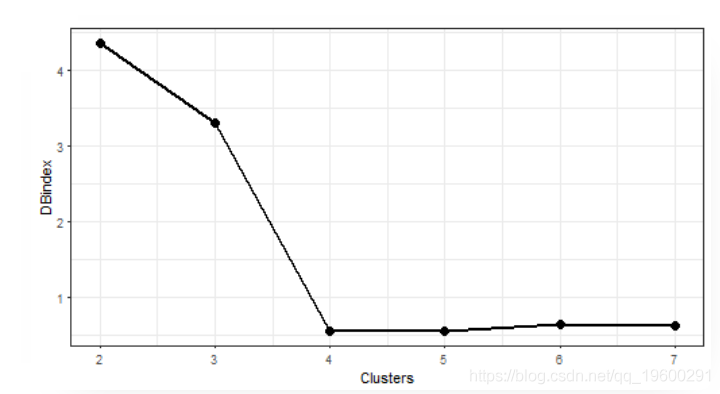
我们可以在4个簇中看到“肘部”。
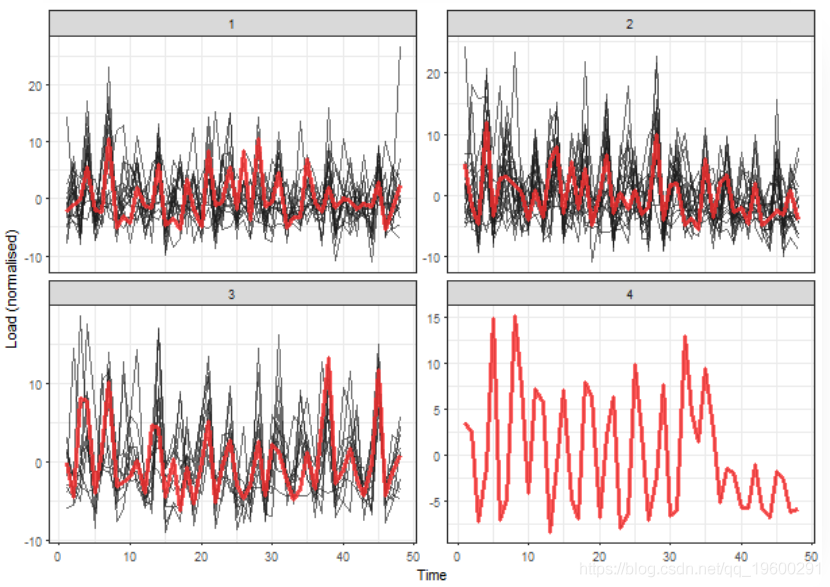
这些结果可以较好解释。因此,基于模型的时间序列表示在此用例中非常有效 。
建议在每天的时间序列中使用与FeaClip一起的窗口方法。最大的优点是不需要与FeaClip方法一起进行标准化。
dim(data_feaclip)## [1] 50 112让我们绘制评估的结果。

我们可以看到现在出现了2个“肘部”。最大的变化是在2到3之间,因此我将选择3。
可分离性好于DFT。但是也可以检查具有不同数量聚类的其他结果。
结论
在本教程中,我展示了如何使用时间序列表示方法来创建用电量的更多特征。然后,用时间序列进行K-medoids聚类,并从创建的聚类中提取典型的负荷曲线。


 Python驱动NIPT数据分析:GAM广义加性模型、Cox生存分析、动态规划、黄金分割法、RF与模糊熵权评价无创产前检测数据时点优化与异常判定 | 附代码数据
Python驱动NIPT数据分析:GAM广义加性模型、Cox生存分析、动态规划、黄金分割法、RF与模糊熵权评价无创产前检测数据时点优化与异常判定 | 附代码数据 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据



