
最近我们被客户要求撰写关于吉布斯采样的研究报告。
我将得出block的Gibbs采样器所需的条件后验分布。
可下载资源
贝叶斯模型
假设我们有一个样本量的主题。 贝叶斯多元回归假设该向量是从多元正态分布中提取的 ,通过使用恒等矩阵,我们假设独立的观察结果。
常用于DBM和DBN,吉布斯采样主要用在像LDA和其它模型参数的推断上。
要完成Gibbs抽样,需要知道条件概率。也就是说,gibbs采样是通过条件分布采样模拟联合分布,再通过模拟的联合分布直接推导出条件分布,以此循环。
概念解释
吉布斯采样是特殊的Metropolis-Hastings算法,会用到马尔科夫链。
具体地说,
MCMC:Markov链通过转移概率矩阵可以收敛到稳定的概率分布。这意味着MCMC可以借助Markov链的平稳分布特性模拟高维概率分布;当Markov链经过burn-in阶段,消除初始参数的影响,到达平稳状态后,每一次状态转移都可以生成待模拟分布的一个样本。
Gibbs抽样是MCMC的一个特例,它交替的固定某一维度,然后通过其他维度的值来抽样该维度的值,注意,gibbs采样只对z是高维(2维以上)(Gibbs sampling is applicable in situations where Z has at least two dimensions)情况有效。
吉布斯采样的通俗解释
Gibbs Sampling就是以一定的概率分布,看发生什么事件。
例子
甲只能E:吃饭、学习、打球,
时间;T:上午、下午、晚上,
天气;W:晴朗、刮风、下雨。
现在要一个sample,这个sample可以是:打球+下午+晴朗。
问题是我们不知道p(E,T,W),或者说,不知道三件事的联合分布joint distribution。当然,如果知道的话,就没有必要用gibbs sampling了。但是,我们知道三件事的conditional distribution。也就是说,p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法,得到联合分布。
具体方法
首先随便初始化一个组合,i.e. 学习+晚上+刮风,
然后依条件概率改变其中的一个变量。
具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习-》吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风-》吃饭+上午+刮风。
同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
二维吉布斯采样算法
吉布斯采样算法中右边的条件概率我们是知道的,例如你要采样的是二维高斯分布,那么固定xt后就是二维高斯分布固定xt后的一维高斯分布,且每次采样的坐标不同,这样这个一维高斯分布概率密度函数也就不一样了。
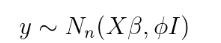
到目前为止,这与 环境中看到的多元正态回归相同。 则将概率最大化可得出以下解 :
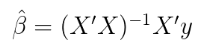
贝叶斯模型是通过指定为一个先验分布得到 。在此示例中,我将在以下情况下使用 先验值
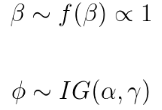
block Gibbs
在对采样器进行编码之前,我们需要导出Gibbs采样器的 每个参数的后验条件分布。
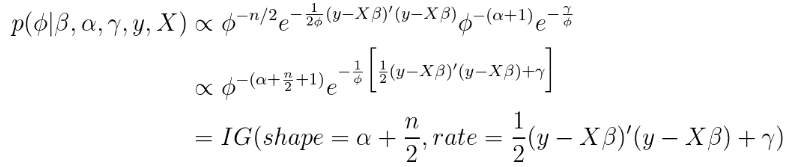
条件后验取更多的线性代数。
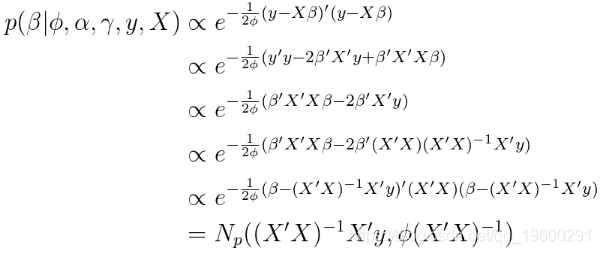
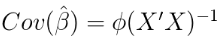
这是一个非常漂亮和直观的结果。 条件后验的协方差矩阵是协方差矩阵的频繁估计,
还要注意,条件后验是一个多元分布,因为它是一个向量。因此,在Gibbs采样器的每次迭代中,我们从后验画出一个完整的矢量 。
模拟
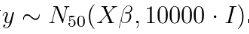
我模拟的 结果向量。
运行 Gibbs采样器 会生成对真实系数和方差参数的估计。运行了500,000次迭代。修整周期为100,000次,修整了10次迭代。
以下是MCMC链的图,其中真实值用红线表示。
# 计算后验摘要统计信息(未在其余代码中使用的统计信息)
post_sum_stats<-post_dist %>%
group_by(param) %>%
summarise(median=median(draw),
lwr=quantile(draw,.025),
upr=quantile(draw,.975)) %>%
mutate(true_vals=c(tb,tphi))
# 合并汇总统计信息
post_dist <- post_dist %>%
left_join(post_sum_stats, by='param')
# 绘制MCMC链
ggplot(post_dist,aes(x=iter,y=draw)) +
geom_line() +
geom_hline(aes(yintercept=true_vals, col='red'), show.legend=FALSE)+
facet_grid(param ~ .,scale='free_y',switch = 'y') +
theme_bw() +
xlab('Gibbs Sample Iteration') + ylab('MCMC Chains') +
ggtitle('Gibbs Sampler MCMC Chains by Parameter')
ggplot(post_dist,aes(x=draw)) +
geom_histogram(aes(x=draw),bins=50) +
geom_vline(aes(xintercept = true_vals,col='red'), show.legend = FALSE) +
facet_grid(. ~ param, scale='free_x',switch = 'y') +
theme_bw() +
xlab('Posterior Distributions') + ylab('Count') +
ggtitle('Posterior Distributions of Parameters (true values in red)')
这是 修整后参数的后验分布:
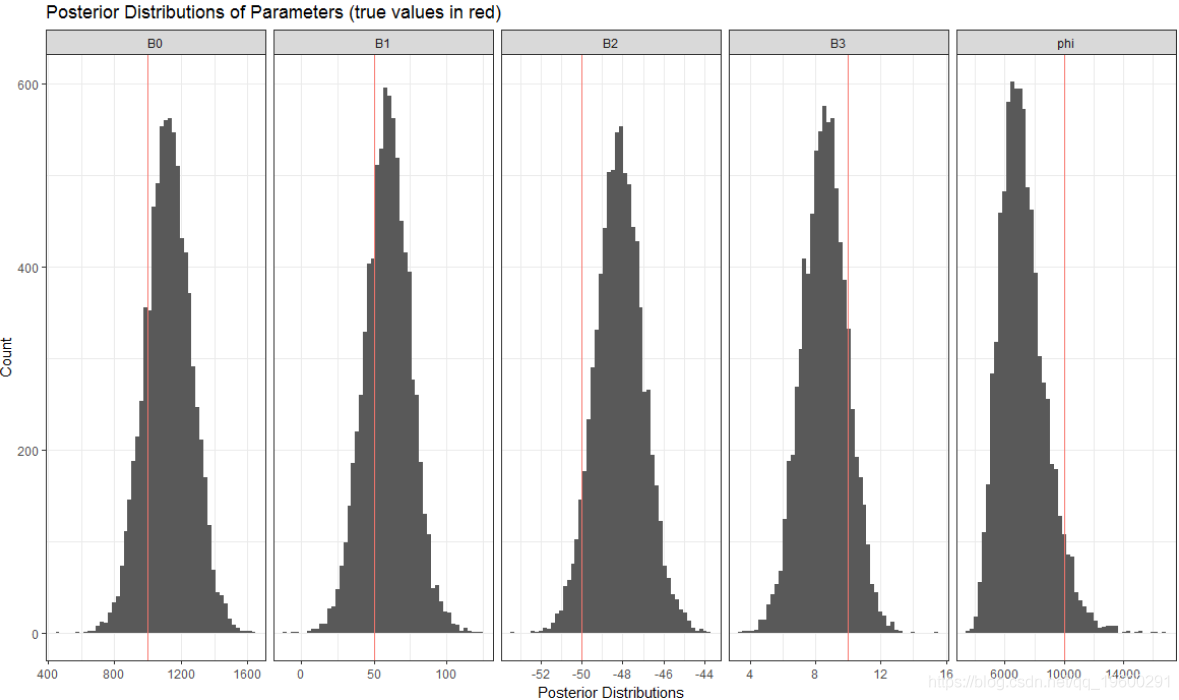
似乎我们能够获得这些参数的合理后验估计。 为了确保贝叶斯估计器正常工作,我对1,000个模拟数据集重复了此练习。
这将产生1,000组后验均值和1,000组95%可信区间。平均而言,这1000个后验均值应以事实为中心。平均而言,真实参数值应在95%的时间的可信区间内。
以下是这些评估的摘要。
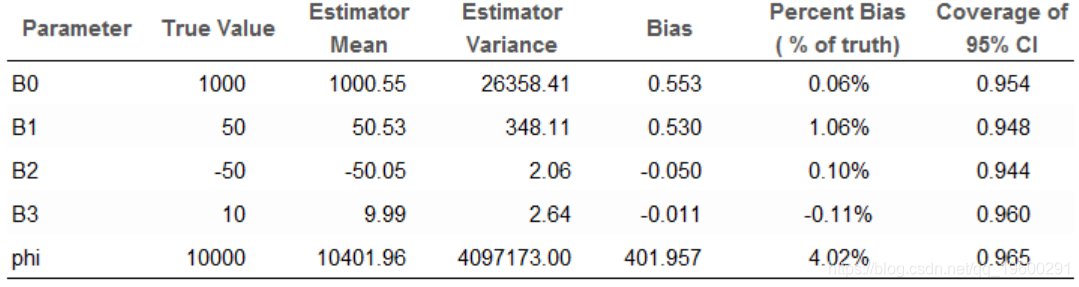
“估计平均值”列是所有1,000个模拟中的平均后验平均值。非常好。偏差百分比均小于5%。对于所有参数,95%CI的覆盖率约为95%。
扩展
我们可以对该模型进行许多扩展。例如,可以使用除正态分布外的其他分布来适应不同类型的结果。 例如,如果我们有二元数据,则可以将其建模为:
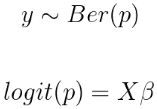
然后在上放一个先验分布。这个想法将贝叶斯线性回归推广到贝叶斯GLM。
在本文中概述的线性情况下,可以更灵活地对协方差矩阵建模。相反,假设协方差矩阵是对角线且具有单个公共方差。这是多元线性回归中的同方差假设。如果数据是聚类的(例如,每个受试者有多个观察结果),我们可以使用反Wishart分布来建模整个协方差矩阵。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践
视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
