在文本挖掘中，我们经常收集一些文档集合，例如博客文章或新闻文章，我们希望将其分成组，以便我们可以分别理解它们。主题建模是对这些文档进行无监督分类的一种方法，类似于对数字数据进行聚类，即使我们不确定要查找什么，也可以找到分组。
潜在狄利克雷分配（LDA）是拟合主题模型特别流行的方法。它将每个文档视为主题的混合体，并将每个主题看作是单词的混合体。
可下载资源
这允许文档在内容方面相互“重叠”，而不是分离成离散的组，以反映自然语言的典型用法。
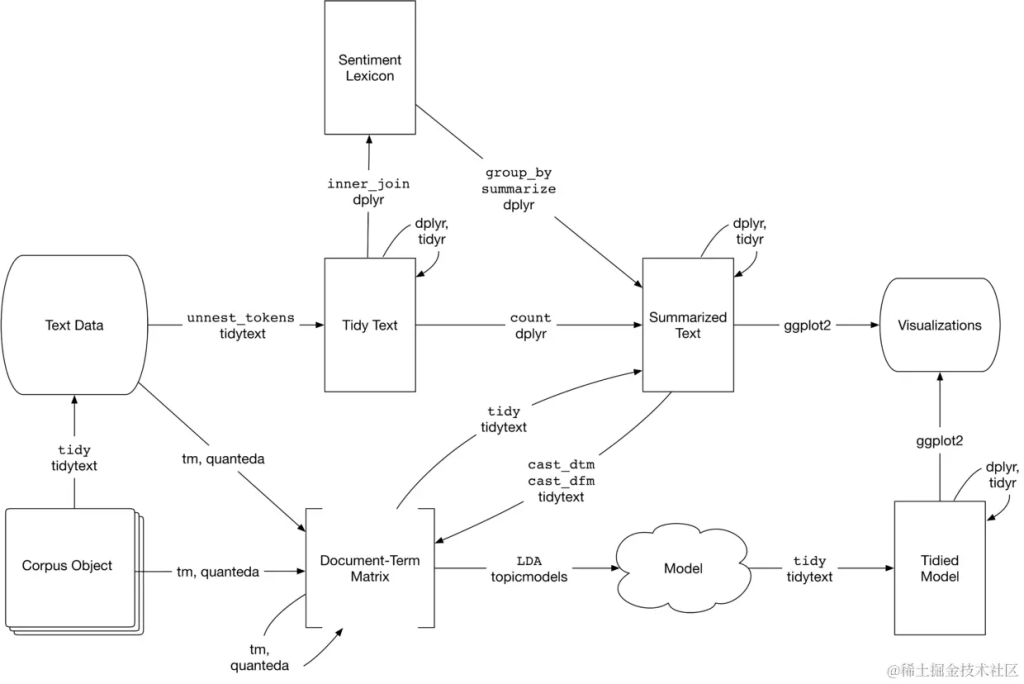
结合主题建模的文本分析流程。topicmodels包采用Document-Term Matrix作为输入，并生成一个可以通过tidytext进行处理的模型，以便可以使用dplyr和ggplot2对其进行处理和可视化。
文本建模的目的是用非常简洁的数学化形式去描述一个语料库中的文本，同时提供文本间、主题间、词语间的统计关系去服务于后续的文本处理工作，比如文本分类、新颖性检测、文本摘要提取、文本相似度测量等。
TF-IDF文本模型是早期文本模型的代表之一，于1983年提出，是基于信息论中著名的TF-IDF公式来对文本进行建模的。TF-IDF公式的计算是对两个部分进行乘积，第一个部分称为词频部分（即TF部分），用来表示文本中某个词在该文本中出现的频率，计算上是用该词在该文本中出现的次数除以该文本包含的词的个数；第二个部分称为逆文本部分（即IDF部分），用来表示在语料库中有多少篇文本包含了这个词，计算上是用总文本数除于含该词的文本数再取对数，两个部分的计算公式以及总的计算公式如下（i代表词语，j代表文本，(i,j)代表第j个文本的第i个词）：
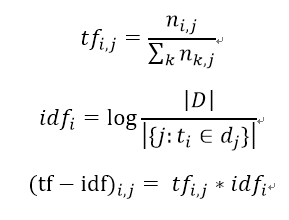
计算好每个词的tf-idf值之后，我们就可以对目标语料库进行建模了。假设语料库中有N篇文档，M个不同的词，那么我们就可以建立一个M * N的矩阵，每一列代表一篇文档，每一行代表某个词在这篇文档中对应的tf-idf值，到此建模就完成啦。我们发现无论每篇包含多少个词，这样建模后每篇文档都被表示成了一个同样长度的向量，向量的每个值就是对应词的tf-idf值。建模矩阵如下图所示：
TF-IDF文本模型总的来说比较简单易懂，对语料库中的文本有着很好的规范化处理，但是它并没有将原有的文本信息压缩了很多，而且单纯地统计词频也没有很好地挖掘词语间、文本间的信息。基于TF-IDF文本模型的缺点，1990年，研究人员提出了LSI文本模型。
LSI文本模型试图将ti-idf的建模矩阵进行奇异值分解，而且是带压缩的分解，分解图示如下：
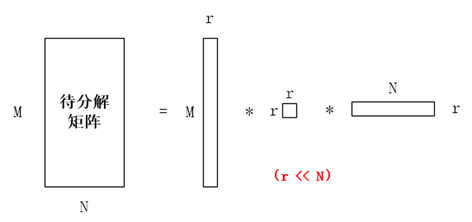
其中r代表了主题的个数，第一个子矩阵代表了词与主题的关系，第二个子矩阵代表了主题本身，第三个子矩阵代表了主题与文档之间的关系。通过这种分解，可以大幅度压缩目标语料库，舍弃无关的信息。同时，LSI的作者也认为LSI模型除了在空间压缩上表现优良外，也可以更好地发掘出同义词以及多义词（可能是通过计算词与词之间坐标的欧几里德距离或者是两个词向量的余弦相似度，这里没有太多探究）。
鉴于矩阵分解的不可解释性，许多研究人员在LSI提出后试图建立其概率图模型的形式，为其提供一个概率形式的解释。Hofmann于1999年提出了pLSI文本模型，是在这方面研究中取得的一个显著的学术成果。接下来，本文将从 概率图模型 的角度以及介绍unigram、mixture of unigrams、pLSI三个概率文本模型。
Unigram文本模型中，文档中的每个词都是从一个单独的多项分布中独立采样而得的，是概率文本模型中最简单的情形，其概率模型图如下所示：
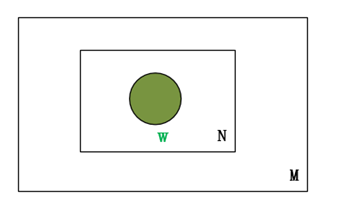
其文本中词语的概率生成公式如下所示：
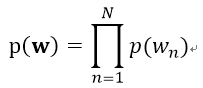
mixture of unigrams文本模型在Unigram文本模型引入了一个服从离散分布的隐变量Z。在这个模型中，文本的生成过程是先选择一个主题z，然后从条件多项分布p(w|z)中独立地生成N个词，以此来构建出文本。该模型的概率模型图如下所示：
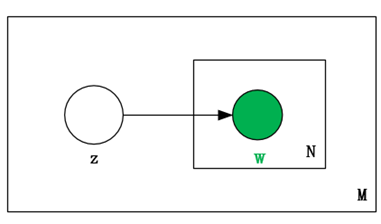
其文本生成的概率公式如下：
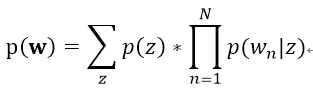
从这个过程中我们可以看出，该模型假定了每篇文档只能属于一个主题，这使得该模型在实际的文本建模中非常受限制，因为一篇文档往往属于多个主题。
pLSI文本模型是在LDA提出之前最“先进”的文本模型，它打破了mixture of unigrams文本模型中“每篇文档只能有一个主题”的束缚，通过引入文本变量来使得对于一个特定的目标文本，可以有多个主题以加权的形式结合在一起。它的概率图模型如下图所示：
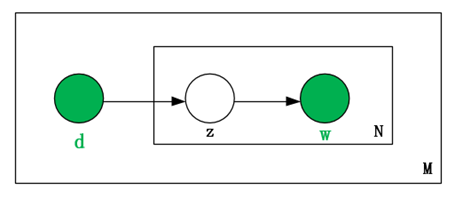
pLSI文本模型的文档、词语的联合生成概率如下：
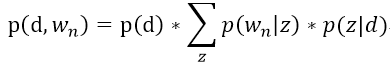
这里我们可以看到，在pLSI中，词语和文档向量都是观测变量，主题的生成取决于文档里面有什么词语。也就是说，在训练这个文本模型的时候，模型里面的主题词只能来自于训练集中的文档，用到测试集的时候可能提取到的主题都是有范围的了，即只能提取出在训练集文档中出现过的词语。所以从这点来看，pLSI文本模型并不是一个泛化能力很好的模型，对于一个里面大部分词都没在训练集文档中出现过的“未知”文档，它会显得很无能为力。pLSI另一个很严重的问题是，由于产生的主题由训练集中文档的信息来决定，所以随着训练集中文档数目的增长，所需要训练的参数也就跟着线性增长，而在机器学习的算法中，参数过多意味着会发生过拟合，这是一个严重的问题。
文本模型的可交换性与LDA的提出动机
在正式开始介绍LDA的建模内容前，我们先了解一下什么是文本模型的可交换性。目前，大多数文本模型都基于“bag-of-words”的假设，即（1）一篇文档内N个词之间的顺序可以随意互换，不影响建模过程；（2）一个语料库内M个文档可以随意互换顺序，哪个文档在前哪个文档在后都无所谓。这两个性质合称为文本模型的可交换性，这一点在德芬涅定理（de Finetti theorem）里面有着更加详细的阐述，本文不再详细展开叙述。
但是需要注意的是，虽然有着文档与文档、一篇文档内词与词之间的可互换性，但是不能跨文档换词，即将文档A中的第a个词与文档B中的第b个词互换，这个不在假设范围之内。
LDA的提出，一方面是受到德菲涅定理的启发，试图将文档间、文档的词语间的可交换性完全发挥出来，在之后介绍的LDA模型中，我们会看到，LDA文本模型将文档的选取、主题的选取、词语的选取都定义为概率生成过程，与上述两个性质相契合；另一方面则是试图去除pLSI的缺陷，让每个单词不再属于单一的一个主题，而主题的种类也不再局限于训练集中文档词语的种类。
潜在狄利克雷分配
潜在Dirichlet分配是主题建模中最常用的算法之一。没有深入模型背后的数学，我们可以理解它是由两个原则指导的。
每个文档都是主题的混合体。我们设想每个文档可能包含来自几个主题的文字，并有一定的比例。例如，在双主题模型中，我们可以说“文档1是90％的主题A和10％的主题B，而文档2是30％的主题A和70％的主题B.”
每个主题都是词汇的混合。例如，我们可以想象一个新闻的两个主题模型，一个话题是“体育”，一个是“娱乐”。体育话题中最常见的词语可能是“篮球”，“足球”和“游泳“，而娱乐主题可以由诸如”电影“，”电视“和”演员“之类的词组成。重要的是，话题可以在话题之间共享; 像“奥运冠军”这样的词可能同时出现在两者中。
LDA是一种同时估计这两种情况的数学方法：查找与每个主题相关的单词集合，同时确定描述每个文档的主题分组。这个算法有很多现有的实现，我们将深入探讨其中的一个。
library(topicmodels)
data("AssociatedPress")
AssociatedPress
: term frequency (tf)我们可以使用LDA()topicmodels包中的函数设置k = 2来创建两个主题的LDA模型。
实际上几乎所有的主题模型都会使用更大的模型k，但我们很快就会看到，这种分析方法可以扩展到更多的主题。
此函数返回一个包含模型拟合完整细节的对象，例如单词如何与主题关联以及主题如何与文档关联。
# # 设置随机种子，使模型的输出是可重复的
ap_lda <- LDA(AssociatedPress,k =2,control =list(seed =1234))
ap_lda拟合模型是“简单部分”：分析的其余部分将涉及使用tidytext软件包中的函数来探索和解释模型。
单词主题概率
tidytext包提供了这种方法来提取每个主题的每个词的概率，称为β。
## # A tibble: 20,946 x 3
## topic term beta
## 1 1 aaron 1.69e-12
## 2 2 aaron 3.90e- 5
## 3 1 abandon 2.65e- 5
## 4 2 abandon 3.99e- 5
## 5 1 abandoned 1.39e- 4
## 6 2 abandoned 5.88e- 5
## 7 1 abandoning 2.45e-33
## 8 2 abandoning 2.34e- 5
## 9 1 abbott 2.13e- 6
## 10 2 abbott 2.97e- 5
## # ... with 20,936 more rows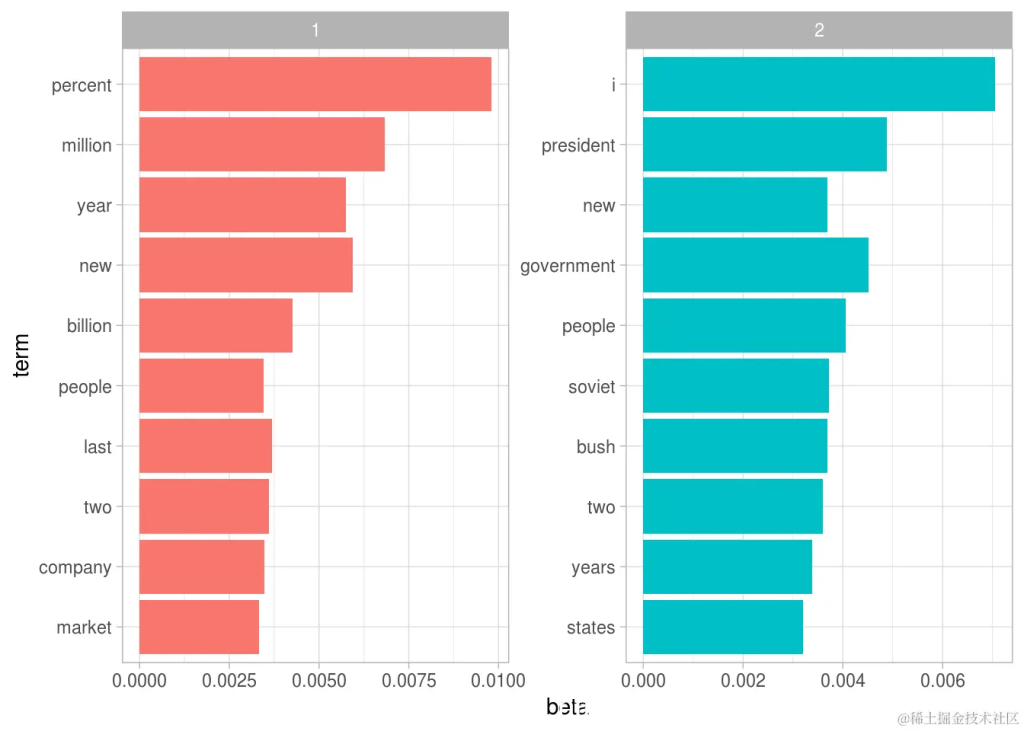每个主题中最常见的词
这种可视化让我们了解从文章中提取的两个主题。话题1中最常见的词语包括“百分比”，“百万”，“十亿”和“公司”，这表明它可能代表商业或财务新闻。话题2中最常见的包括“总统”，“政府”，表示这个话题代表政治新闻。关于每个主题中的单词的一个重要观察是，在这两个主题中，诸如“新”和“人”等一些词语是常见的。与“硬聚类”方法相反，这是话题建模的优势：自然语言中使用的话题可能存在一些重叠。
我们可以认为最大的区别是两个主题之间β差异最大的词。
## # A tibble: 198 x 4
## term topic1 topic2 log_ratio
##
## 1 administration 0.000431 0.00138 1.68
## 2 ago 0.00107 0.000842 -0.339
## 3 agreement 0.000671 0.00104 0.630
## 4 aid 0.0000476 0.00105 4.46
## 5 air 0.00214 0.000297 -2.85
## 6 american 0.00203 0.00168 -0.270
## 7 analysts 0.00109 0.000000578 -10.9
## 8 area 0.00137 0.000231 -2.57
## 9 army 0.000262 0.00105 2.00
## 10 asked 0.000189 0.00156 3.05
## # ... with 188 more rows图显示了这两个主题之间差异最大的词。
我们可以看到，话题2中更常见的词包括“民主”和“共和党”等政党等政治家的名字。主题1的特点是“日元”和“美元”等货币以及“指数”，“价格”和“利率”等金融术语。这有助于确认算法确定的两个主题是政治和财务新闻。
随时关注您喜欢的主题
文档 – 主题概率
除了将每个主题评估为单词集合之外，LDA还将每个文档建模为混合主题。我们可以检查每个文档的每个主题概率，称为γ（“伽玛”） 。
## # A tibble: 4,492 x 3
## document topic gamma
## <int> <int> <dbl>
## 1 1 1 0.248
## 2 2 1 0.362
## 3 3 1 0.527
## 4 4 1 0.357
## 5 5 1 0.181
## 6 6 1 0.000588
## 7 7 1 0.773
## 8 8 1 0.00445
## 9 9 1 0.967
## 10 10 1 0.147
## # ... with 4,482 more rows这些值中的每一个都是该文档中从该主题生成的单词的估计比例。例如，该模型估计文档1中单词的大约24.8％是从主题1生成的。
我们可以看到，这些文档中的许多文档都是从两个主题中抽取出来的，但文档6几乎完全是从主题2中得出的，其中有一个主题1γ接近零。为了检查这个答案，我们可以检查该文档中最常见的词。
#> # A tibble: 287 x 3
#> document term count
#> <int> <chr> <dbl>
#> 1 6 noriega 16
#> 2 6 panama 12
#> 3 6 jackson 6
#> 4 6 powell 6
#> 5 6 administration 5
#> 6 6 economic 5
#> 7 6 general 5
#> 8 6 i 5
#> 9 6 panamanian 5
#> 10 6 american 4
#> # … with 277 more rows根据最常见的词汇，可以看出该算法将其分组到主题2（作为政治/国家新闻）是正确的。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
PCA主成分分析原理与水果成熟状态数据分析实例：Python中PCA-LDA与卷积神经网络CNN
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
R语言逻辑回归、GAM、LDA、KNN、PCA主成分分析分类预测房价及交叉验证
R语言汽车口碑数据采集抓取、文本数据分词和词云可视化实现
