最近我们被客户要求撰写关于使用长短期记忆网络（LSTM）来拟合一个不稳定的时间序列的研究报告。
每年的降雨量数据可能是相当不稳定的。与温度不同，温度通常在四季中表现出明显的趋势，而雨量作为一个时间序列可能是相当不稳定的。
夏季的降雨量与冬季的降雨量一样多是很常见的。
LSTM 的核心要素是细胞状态，即贯穿下图顶部的水平线。细胞状态有点像传送带。它沿着整个链直线贯通，只有一些微小的线性相互作用。信息很容易在没有大幅变化的情况下流动。在传递过程中，通过当前时刻输入 、上一时刻隐藏层状态
、上一时刻细胞状态
以及门结构来增加或删除细胞状态中的信息。
门是指一种有选择性地让信息通过的方式，即控制增加或删除信息的程度。其由一个 sigmoid 神经网络层和一个点乘运算组成。
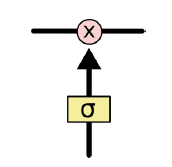
sigmoid 层输出 到
之间的数字，描述每个组件应该允许的通过量。
的值表示“不让任何量通过”，而
的值表示“让所有量通过”。
LSTM 有三个这样的门，用来保护以及控制细胞的状态。
逐步解析LSTM
遗忘门：
LSTM 的第一步是决定从上一个细胞状态中丢弃什么信息。这个决定是由一个叫做“遗忘门”的 sigmoid 层做出的。如下图所示，遗忘门的输入为 和
，输出为
。即为细胞状态
中的每个值输出一个相对应的介于
和
之间的值。
表示完全保留，而
表示完全删除。
让我们回到语言模型的例子，即试图根据前面的单词预测下一个单词。在这种情况下，细胞状态可能包含了当前主题的性别特征，以便正确使用代词。然而当我们看到一个新的主题时，我们通常需要忘掉旧主题的性别特征。
输入门：
下一步是决定在细胞状态中存储哪些新信息。这分为两个部分。首先， 层创建一个新的打算添加到细胞状态中的候选值向量。其次，一个名为“输入门层”的 sigmoid 层决定候选值中的哪些值应该被添加到细胞状态中。接下来，我们将二者结合来创建细胞状态的更新值。
在我们语言模型的例子中，我们想要在细胞状态中添加新主题的性别特征，以取代我们打算遗忘的旧主题的性别特征。
更新细胞状态：
现在是时候将旧的单元格状态 更新为新的细胞状态
了。前面的步骤已经定好了要做什么，接下来我们只需要实际去做就好了。
我们将旧状态 按元素乘上
，将打算遗忘的内容遗忘掉。同理，我们添加
，即添加新的信息到细胞状态中。
相对于语言模型，这样的操作所达到的目的正是删除旧主题的性别信息并添加新信息，正如我们之前所决定的那样。
输出门：
最后，我们将决定输出什么。此输出将基于细胞状态，但将是基于更新后的细胞状态。首先，我们运行一个 sigmoid 层，它决定输出细胞状态的哪些部分。然后，我们使细胞状态通过 （将值的范围缩小在
和
之间)，并将其乘以 sigmoid 层的输出，这样我们只输出了我们想要输出的部分。
对于语言模型示例，由于它只看到了一个主语，所以它可能希望输出与动词相关的信息，以应对接下来发生的事情。例如，它可能输出主语是单数还是复数，这样我们就能知道后面跟着的与其相对应的动词的形式。
穿越时间的反向传播
以上所述是 LSTM 的前向计算过程，接下来我们要关注的是求解梯度的反向传播算法。
结合上述，我们可以整理思路如下：
-
前向计算各时刻遗忘门
、输入门
以及根据当前输入得到的新信息候选值
、细胞状态
、输出门
、隐藏层状态
、最终模型的输出
；
-
反向传播计算误差
，即模型目标函数
对加权输入
的偏导；（注意：
的反向传播）；
-
求解模型目标函数
，
，
；
，
，
；
，
，
；
，
，
；
，
的偏导数。
传播至输入层更新参数：
首先我们定义 ，且由上述公式可知
，因此可得:
；
同理可得：
。
注意，由于 记忆了所有时刻的细胞状态，故每个时间点迭代时，
累加。
由于 ，因此可得 :
，
，
，
。
由于：
;
；
；
。
因此：
；
；
；
。
最后，可以求得各个权重矩阵的偏导数（注：下述公式中的上标 表示矩阵的转置）：
，
，
；
，
，
；
，
，
；
，
，
；
注意，以上权重参数在所有时刻共享，故每个时间点迭代时的梯度累加。
穿越时间反向传播：
沿时间反向传播，就是要计算出 时刻的误差项
。
我们可以得到：
。
且已知：
；
。
并且已知 、
、
、
都是
的函数，那么，利用全导数公式可得：
接下来，我们把上式中的每个偏导数都求出来，
根据：
；
以及：
；
；
。
可得：
；
；
；
；
；
；
；
；
；
；
；
；
；
将上述所得公式代入到公式 ，可以得到：
其中：
；
；
；
。
即为误差沿着时间传播一个时刻的公式。有了它，我们就可以写出将误差项反向传播到任意
时刻的公式：
。
下面是某地区2020年11月降雨量的图解。
作为一个具有连续性的神经网络架构，长短期记忆（LSTM）模型在解释时间序列的波动性方面展现出了显著的优势。LSTM模型特别适用于处理具有长期依赖关系的时间序列数据，它能够有效地捕捉序列中的复杂模式和动态变化。这种能力使得LSTM模型在分析和预测时间序列的波动性时具有独特的优势。
为了验证LSTM模型在解释时间序列波动性方面的有效性，我们可以采用统计检验方法，如Ljung-Box检验。该检验通过计算时间序列中自相关系数的联合统计量来评估序列中是否存在显著的随机性。如果Ljung-Box检验的p值小于0.05，这意味着在统计上具有显著性，即时间序列中的残差表现出随机模式。这种随机性进一步说明了时间序列中存在明显的波动性，而这正是LSTM模型所擅长捕捉的特性。
>>> sm.stats.acorr_ljungbox(res.resid, lags=\[10\])
可下载资源
作者
Ljung-Box检验
Dickey-Fuller 检验
数据操作和模型配置
该数据集由722个月的降雨量数据组成。
选择712个数据点用于训练和验证，即用于建立LSTM模型。然后，过去10个月的数据被用来作为测试数据，与LSTM模型的预测结果进行比较。
下面是数据集的一个片段。
然后形成一个数据集矩阵，将时间序列与过去的数值进行回归。
# 形成数据集矩阵 for i in range(len(df)-previous-1): a = df\[i:(i+previous), 0\] dataX.append(a) dataY.append(df\[i + previous, 0\])
然后用MinMaxScaler对数据进行标准化处理。
将前一个参数设置为120，训练和验证数据集就建立起来了。作为参考，previous = 120说明模型使用从t – 120到t – 1的过去值来预测时间t的雨量值。
随时关注您喜欢的主题
前一个参数的选择要经过试验，但选择120个时间段是为了确保识别到时间序列的波动性或极端值。
# 训练和验证数据的划分 train_size = int(len(df) * 0.8) val\_size = len(df) - train\_size train, val = df\[0:train\_size,:\], df\[train\_size:len(df),:\]# 前期的数量 previous = 120
然后，输入被转换为样本、时间步骤、特征的格式。
# 转换输入为\[样本、时间步骤、特征\]。 np.reshape(X_train, (shape\[0\], 1, shape\[1\]))
模型训练和预测
该模型在100个历时中进行训练，并指定了712个批次的大小（等于训练和验证集中的数据点数量）。
# 生成LSTM网络 model = tf.keras.Sequential() # 列出历史中的所有数据 print(history.history.keys()) # 总结准确度变化 plt.plot(history.history\['loss'\])
下面是训练集与验证集的模型损失的关系图。
预测与实际降雨量的关系图也被生成。
# 绘制所有预测图 plt.plot(valpredPlot)
预测结果在平均方向准确性（MDA）、平均平方根误差（RMSE）和平均预测误差（MFE）的基础上与验证集进行比较。
mda(Y_val, predictions)0.9090909090909091 >>> mse = mean\_squared\_error(Y_val, predictions) >>> rmse = sqrt(mse) >>> forecast_error >>> mean\_forecast\_error = np.mean(forecast_error)
- MDA: 0.909
- RMSE: 48.5
- MFE: -1.77
针对测试数据进行预测
虽然验证集的结果相当可观，但只有将模型预测与测试（或未见过的）数据相比较，我们才能对LSTM模型的预测能力有合理的信心。
如前所述，过去10个月的降雨数据被用作测试集。然后，LSTM模型被用来预测未来10个月的情况，然后将预测结果与实际值进行比较。
至t-120的先前值被用来预测时间t的值。
# 测试（未见过的）预测 np.array(\[tseries.iloctseries.iloc,t
获得的结果如下
- MDA: 0.8
- RMSE: 49.57
- MFE: -6.94
过去10个月的平均降雨量为148.93毫米，预测精度显示出与验证集相似的性能，而且相对于整个测试集计算的平均降雨量而言，误差很低。
结论
在这个例子中，你已经看到:
- 如何准备用于LSTM模型的数据
- 构建一个LSTM模型
- 如何测试LSTM的预测准确性
- 使用LSTM对不稳定的时间序列进行建模的优势
【视频】R语言支持向量回归SVR预测水位实例讲解|附代码数据
数据分享|R语言Python机器学习预测4案例合集：众筹平台、机票折扣、糖尿病患者、员工满意度
R语言神经网络模型金融应用预测上证指数时间序列可视化
