
线性回归在财务中被广泛应用于众多应用程序中。
我们将使用线性回归来估计股票价格。
可下载资源
线性回归是一种用于模拟因变量(y)和自变量(x)之间关系的方法。通过简单的线性回归,只有一个自变量x。可能有许多独立变量属于多元线性回归的范畴。在这种情况下,我们只有一个自变量即日期。对于第一个日期上升到日期向量长度的整数,该日期将由1开始的整数表示,该日期可以根据时间序列数据而变化。当然,我们的因变量将是股票的价格。为了理解线性回归,您必须了解您可能在学校早期学到的相当基本的等式。
一元线性回归的基本假设有
1、随机误差项是一个期望值或平均值为0的随机变量;
2、对于解释变量的所有观测值,随机误差项有相同的方差;
3、随机误差项彼此不相关;
4、解释变量是确定性变量,不是随机变量,与随机误差项彼此之间相互独立;
5、解释变量之间不存在精确的(完全的)线性关系,即解释变量的样本观测值矩阵是满秩矩阵;
6、随机误差项服从正态分布
违背基本假设的计量经济学模型还是可以估计的,只是不能使用普通最小二乘法进行估计。
当存在异方差时,普通最小二乘法估计存在以下问题: 参数估计值虽然是无偏的,但不是最小方差线性无偏估计。
杜宾-瓦特森(DW)检验,计量经济,统计分析中常用的一种检验序列一阶 自相关 最常用的方法。
所谓多重共线性(Multicollinearity)是指线性回归模型中的解释变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。影响
(1)完全共线性下参数估计量不存在
(2)近似共线性下OLS估计量非有效
多重共线性使参数估计值的方差增大,1/(1-r2)为方差膨胀因子(Variance Inflation Factor, VIF)
(3)参数估计量经济含义不合理
(4)变量的显著性检验失去意义,可能将重要的解释变量排除在模型之外
(5)模型的预测功能失效。变大的方差容易使区间预测的“区间”变大,使预测失去意义。
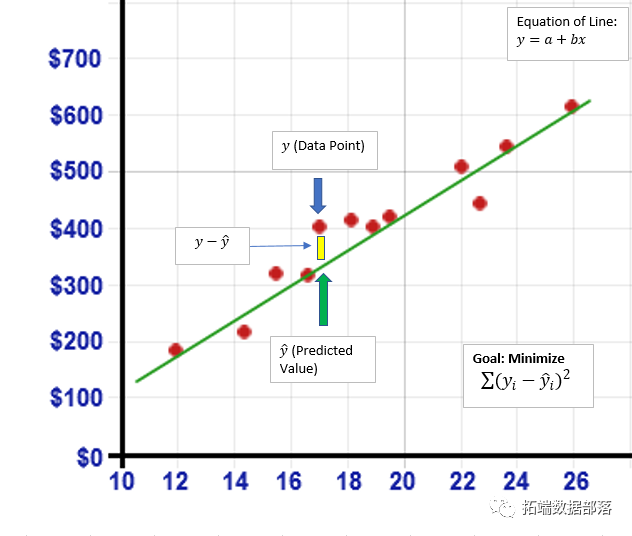
y = a + bx
- Y =预测值或因变量
- b =线的斜率
- x =系数或自变量
- a = y截距
从本质上讲,这将构成我们对数据的最佳拟合。在OLS过程中通过数据集绘制了大量线条。该过程的目标是找到最佳拟合线,最小化平方误差和(SSE)与股票价格(y)的实际值以及我们在数据集中所有点的预测股票价格。这由下图表示。对于绘制的每条线,数据集中的每个点与模型输出的相应预测值之间存在差异。将这些差异中的每一个加起来并平方以产生平方和。从列表中,我们采用最小值导致我们的最佳匹配线。考虑下图:
第一部分:获取数据:
from matplotlib import style
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import quandl
import datetime
style.use('ggplot')
#日期
start_date = datetime.date(2017,1,3)
t_date=start_date, end_date=end_date, collapse="daily")
df = df.reset_index()
prices = np.reshape(prices, (len(prices), 1))第二部分:创建一个回归对象:
linewidth=3, label = 'Predicted Price') #绘制线性回归线
plt.title('Linear Regression | Time vs. Price')
plt.legend()
predicted_price =regressor.predict(date)
输出:
预测日期输入价格:
创建训练/测试集
xtrain, x , ytrain)
#训练
plt.title('Linear Regression | Time vs. Price')
#测试集图
plt.scatter(xtest, ytest, color='yellow', label= 'Actual Price') #绘制初始数据点
plt.plot(xtest, regressor.predict(xtest), color='blue', linewidth=3, label = 'Predicted Price') #绘图
plt.show()输出:
测试集:
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测 专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察
专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 专题|Python贝叶斯金融数据应用实例合集:随机波动率SV模型、逻辑回归、参数更新、绩效比较BEST分析亚马逊股票、标准普尔500指数|附数据代码
专题|Python贝叶斯金融数据应用实例合集:随机波动率SV模型、逻辑回归、参数更新、绩效比较BEST分析亚马逊股票、标准普尔500指数|附数据代码
