步骤1加载数据并拟合模型

加载工具箱附带的纳斯达克数据。将条件均值和方差模型拟合到数据中。

 
 
nasdaq = DataTable.NASDAQ;
r = price2ret(nasdaq);
N = length(r);
fit = estimate(mode ,r,'Variance0',{'Constant0',0.001});
 
    ARIMA(1,0,0) Model (t Distribution):
 
                  Value      StandardError    TStatistic      PValue  
                _________    _____________    __________    __________
 
    Constant    0.0012326     0.00018163         6.786      1.1528e-11
    AR{1}        0.066389       0.021398        3.1026       0.0019182
    DoF            14.839         2.2588        6.5693      5.0539e-11
 
 
 
    GARCH(1,1) Conditional Variance Model (t Distribution):
 
                  Value       StandardError    TStatistic      PValue  
                __________    _____________    __________    __________
    Constant    3.4488e-06     8.3938e-07        4.1087      3.9788e-05
    GARCH{1}       0.82904       0.015535        53.365               0
    ARCH{1}        0.16048       0.016331        9.8268      8.6333e-23
    DoF             14.839         2.2588        6.5693      5.0539e-11
[E0,V0] = infer(fit,r);

AR模型：自回归模型，是一种线性模型.AR模型是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据（设推出P点），所以其本质类似于插值。

MA模型：移动平均法模型，其中使用趋势移动平均法建立直线趋势的预测模型

ARMA模型：自回归滑动平均模型，拟合较高阶模型.模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法。它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。

GARCH模型：广义回归模型，对误差的方差建模，适用于波动性的分析和预测.是ARCH模型的拓展， GARCH对误差的方差进行了进一步的建模，特别适用于波动性的分析和预测。

第2步预测收益和条件差异

使用forecast计算收益率：条件方差为1000周期的未来数据的MMSE预测。

使用观察到的收益率和推断残差以及条件方差作为预采样数据。

[Y,YMS E,V] = forecast(fit, 100 0,'Y 0',r,'E0', E0, 'V0' ,V0);
upper = Y + 1.96*sqrt(YMSE);
lower = Y - 1.96*sqrt(YMSE);
 
figure
subplot(2,1,1)
plot(r,'Color',[.75,.75,.75])
hold on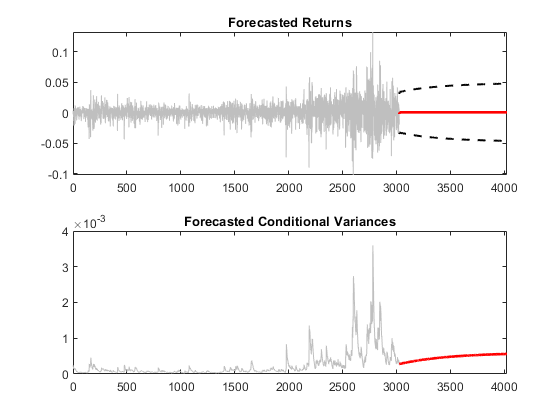

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.GARCH（1,1），MA以及历史模拟法的VaR比较

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.matlab预测ARMA-GARCH 条件均值和方差模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略

条件方差预测收敛于GARCH条件方差模型的渐近方差。预测的收益收敛于估计的模型常数（AR条件均值模型的无条件均值）。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！