本文应用R软件技术,分别利用logistic模型、ARFMA模型、ARIMA模型、时间序列模型对从2016到2100年的世界人口进行预测。
作者将1950年到2015年的历史数据作为训练集来预测85年的数据。模型稳定性经过修正后较好,故具有一定的参考价值。
可下载资源
随着时间的推移,世界人口不断的增长,为了更好地把握世界人口的进展速度与规律。
我们利用建立logistic模型并运用R语言软件来分析并预测在2100年世界的人口数,并与预测出的数据做对比,看模型构造的好坏并进行模型改进与扩展。
模型一:logistic模型
logistic模型又称作阻滞增长模型,主要用来描述在环境资源有限制的情况下,人口数量的增长规律。由于一些因素的影响世界人口数量最终会达到一个饱和值。阻滞作用上体现在对的影响上,使得随着年份的增加而下降。若将表示为的函数,则它应是减函数。则有
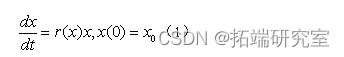
由于bgistic回归模型就是基于二项分布族的广义线性模型,因此在R软件中,Logistic回归分析可以通过调用广义线性回归模型函数glm()来实现,其调用格式为
Log<一glm(formula,family=binomial,data)其中,formula为要拟合的模型,family=binomial说明分布为二项分布,data为可选择的数据框。
我们将1950年到2100年的人口数据进行录入,并调用glmnet包来进行拟合。
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
视频
在Python和R语言中建立EWMA,ARIMA模型预测时间序列
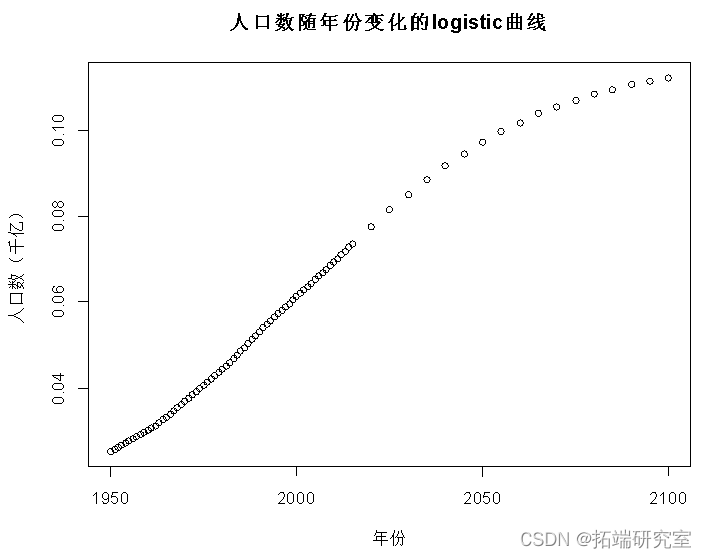
summary(lg.glm) plot(x, y, main = "人口数随年份变化的logistic曲线",xlab = "年份", ylab = "人口数(千亿)")
Deviance Residuals: Min 1Q Median 3Q Max -0.089181 -0.028946 0.002154 0.027206 0.042212 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -23.76776 22.17527 -1.072 0.284 x 0.01046 0.01101 0.950 0.342 (Dispersion parameter for binomial family taken to be 1) Null deviance: 0.923810 on 82 degrees of freedom Residual deviance: 0.082928 on 81 degrees of freedom AIC: 13.991 Number of Fisher Scoring iterations: 6
从检验结果可看出随着时间的推移能影响人口的数量,并且年份越大,人口密度越大;最终会停留到一个饱和值,并得到logistic回归模型:
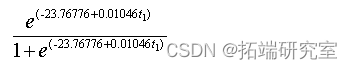
模型二: AFRIMA模型
时间序列模型可分为段记忆模型和长记忆模型。一般的时间序列分析模型有自回归(AR)模型、滑动平均(MA)模型、自回归滑动平均(ARMA)模型、自回归整合滑动平均(ARIMA)模型等,这些模型主要是短记忆模型。
目前,人们对宏观经济变量的实证研究发现,长记忆模型虽然远距离观测值间的相依性很小但是仍具有研究价值。分整自回归移动平均模型(ARFMA)模型是长记忆模型,它是由Granger和Joyeux (1980)以及Hosking (1981)在ARIMA模型的基础上构建的,广泛应用于经济金融领域。
AFRIMA模型定义
AFRIMA模型的基于A R M A模型和ARIMA模型。
ARMA(p,q),模型的形式为:
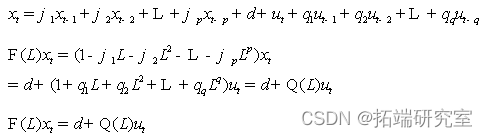
模型实现:
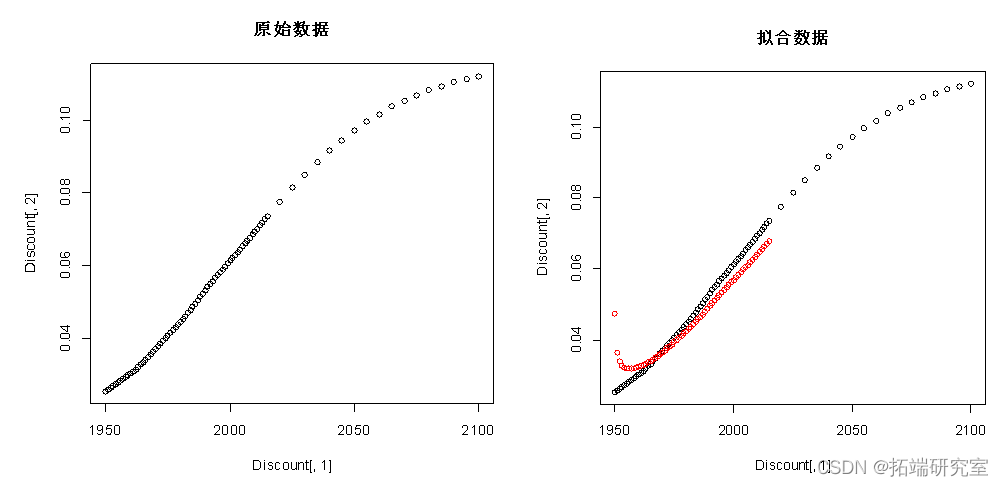
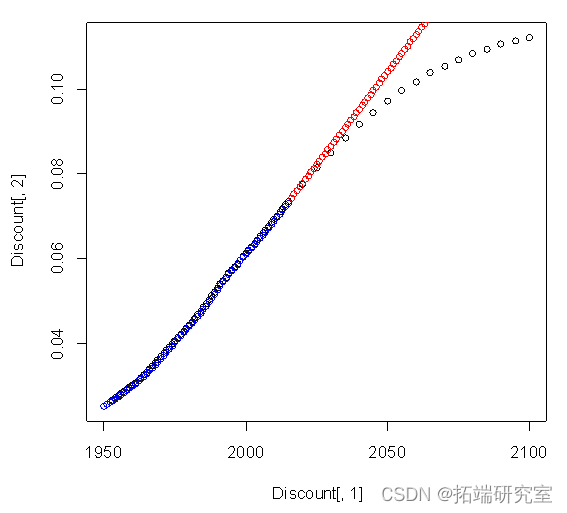
arfi(Diut\[,2\]\[)#建立arfima模型 plot(Discnt\[,1\],Dscunt\[,2\])#原始数据 points(Dicount\[,1\]\[1:66\],f$fittedcol="red")#拟合数据
随时关注您喜欢的主题
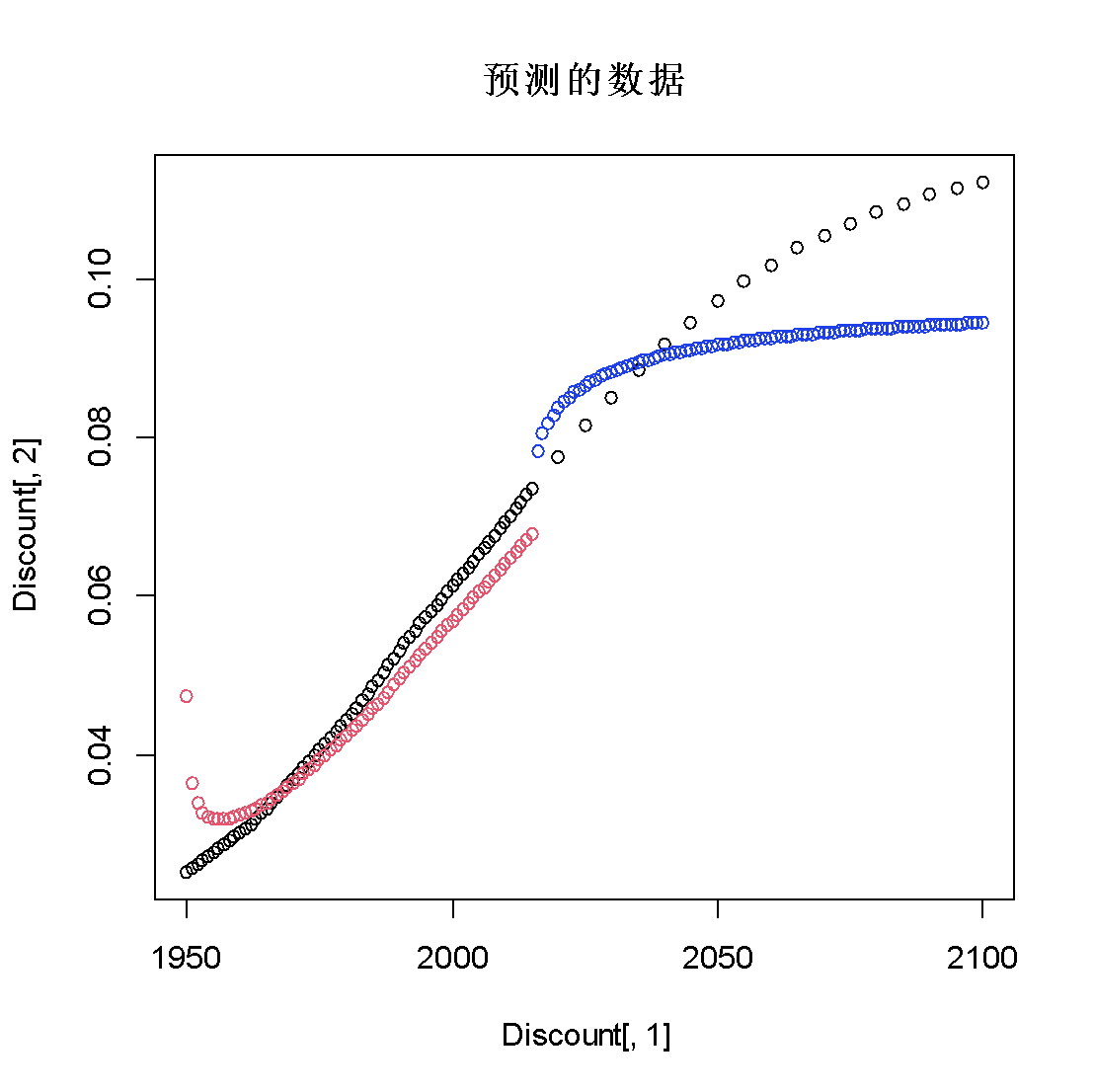
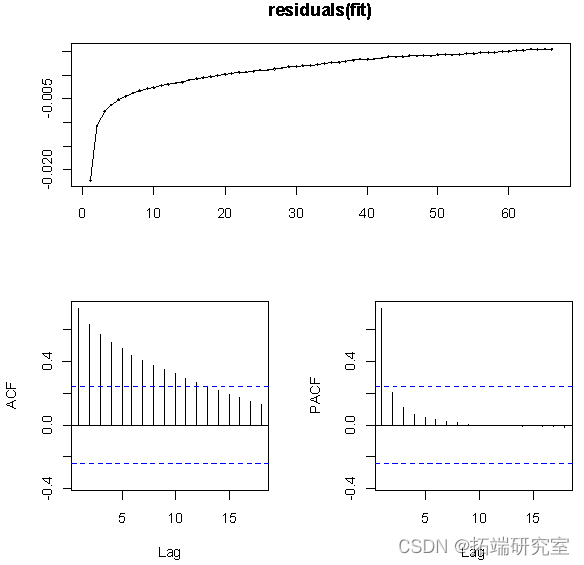
从残差图的结果来看,ACF的值不在虚线范围内,即残差不平稳,不是白噪声,因此下面对数据进行一阶差分。
模型稳定性改进
对数据进行一阶差分使数据更加稳定。
从残差图的结果来看,ACF的值和PACF的值都在虚线范围内,即残差平稳,因此模型稳定。
points(c(2016:2100), diffinv(pre$mean)\[-1\]+ Discount\[66,2\],col="blue")
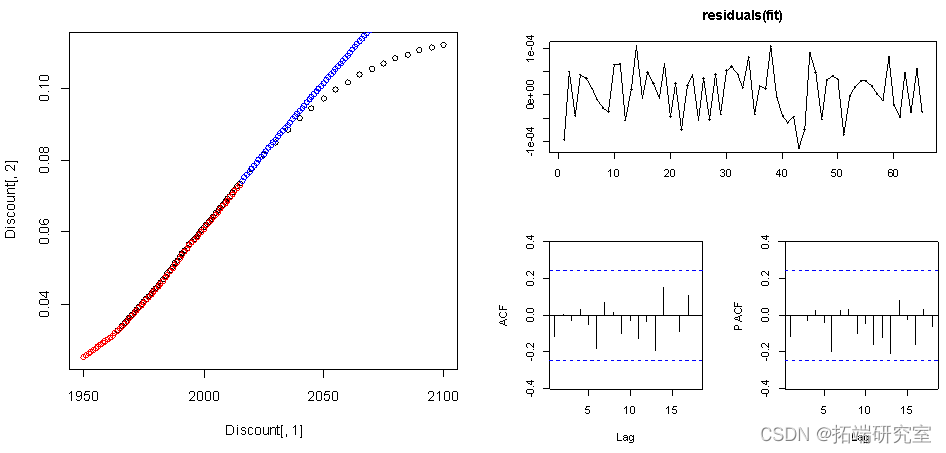
模型三: ARIMA模型
ARIMA模型定义
ARIMA模型全称为差分自回归移动平均模型。是由博克思和詹金斯于70年代初提出的一著名时间序列预测方法,博克思-詹金斯法。其中ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归,p为自回归项;MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。
ARIMA模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。
ARIMA模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。
建模过程主要包括:
第一步:自回归过程
令Yt表示t时期的GDP。如果我们把Yt的模型写成
(Y\_t-δ)=α\_1 (Y_(t-1)-δ)+u_t
其中δ是Y的均值,而ut是具有零均值和恒定方差σ^2的不相关随机误差项(即ut是白噪音),则成Yt遵循一个一阶自回归或AR(1)随机过程。
P阶自回归函数形式写成:
(Y\_t-δ)=α\_1 (Y_(t-1)-δ)+α\_2 (Y\_(t-2)-δ)+α\_3 (Y\_(t-3)-δ)+⋯+α\_p2 (Y\_(t-p)-δ)+u_t
模型中只有Y这一个变量,没有其他变量。可以理解成“让数据自己说话”。
第二步:移动平均过程
上述AR过程并非是产生Y的唯一可能机制。如果Y的模型描述成
Y\_t=μ+β\_0 u\_t+β\_1 u_(t-1)
其中μ是常数,u为白噪音(零均值、恒定方差、非自相关)随机误差项。t时期的Y等于一个常数加上现在和过去误差项的一个移动平均值。则称Y遵循一个一阶移动平均或MA(1)过程。
q阶移动平均可以写成:
Y\_t=μ+β\_0 u\_t+β\_1 u_(t-1)+β\_2 u\_(t-2)+⋯+β\_q u\_(t-q)
自回归于移动平均过程
如果Y兼有AR和MA的特性,则是ARMA过程。Y可以写成
Y\_t=θ+α\_1 Y_(t-1)+β\_0 u\_t+β\_1 u\_(t-1)
其中有一个自回归项和一个移动平均项,那么他就是一个ARMA(1,1)过程。Θ是常数项。
ARMA(p,q)过程中有p个自回归和q个移动平均项。
第三步:自回归求积移动平均过程
上面所做的都是基于数据是平稳的,但是很多时候时间数据是非平稳的,即是单整(单积)的,一般非平稳数据经过差分可以得到平稳数据。因此如果我们讲一个时间序列差分d次,变成平稳的,然后用AEMA(p,q)模型,则我们就说那个原始的时间序列是AEIMA(p,d,q),即自回归求积移动平均时间序列。AEIMA(p,0,q)=AEMA(p,q)。
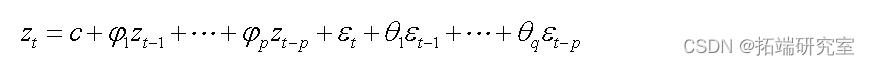
通常,ARIMA 模型建模步骤有4个阶段: 序列平稳性检验,模型初步识别,模型参数估计和模型诊断分析。
模型实现
步骤一:识别。找出适当的p、d、和q值。通过相关图和偏相关图可以解决。
步骤二:估计。估计模型周所含自回归和移动平均项的参数。有时可以用最小二乘法,有时候需要用非线性估计方法。(软件可以自动完成)
步骤三:诊断(检验)。看计算出来的残差是不是白噪音,是,则接受拟合;不是,则重新在做。
步骤四:预测。短期更为可靠。
具体来说:
首先,看一下有没有很明显的trend,需不需要differencing之后再建模。
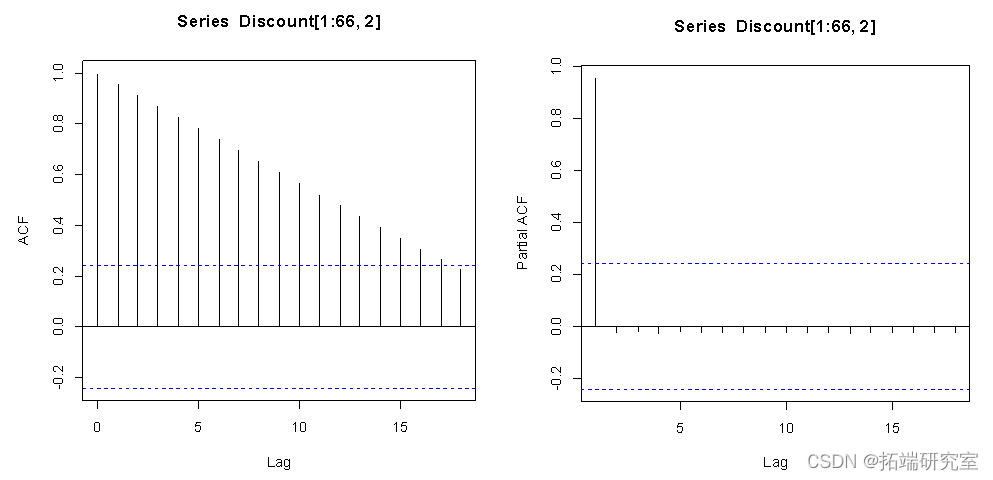
从ACF和PACF的结果来看,序列没有很快地落入虚线范围之内,因此,序列不平稳。对序列进行差分。
画出ACF 和PACF,通过看图来决定用哪个模型(ARMA(p,q),ARIMA之类的)。
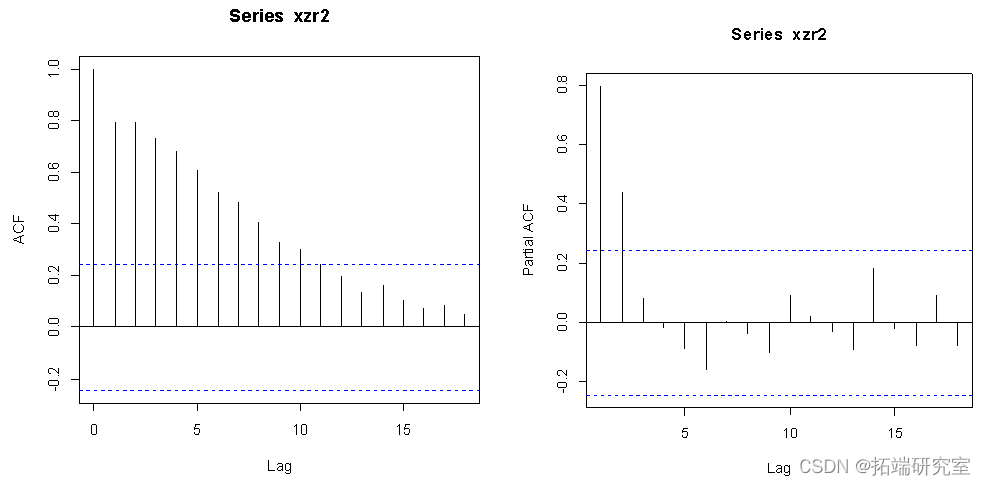
从差分后的数据结果来看,ACF在8阶后开始落入虚线范围,PACF在2阶后很快落入虚线范围,因此p=8,q=2,d=1。
xz1=automa(Dist\[1:66,2\],ic=c('bic'),trace=T)#自动查找最优的arima模型
ARIMA(2,2,2) : -1058.701 ARIMA(0,2,0) : -1026.504 ARIMA(1,2,0) : -1049.834 ARIMA(0,2,1) : -1048.83 ARIMA(1,2,2) : -1062.532 ARIMA(1,2,1) : -1050.673 ARIMA(1,2,3) : -1058.723 ARIMA(2,2,3) : Inf ARIMA(0,2,2) : -1060.99 Best model: ARIMA(1,2,2)
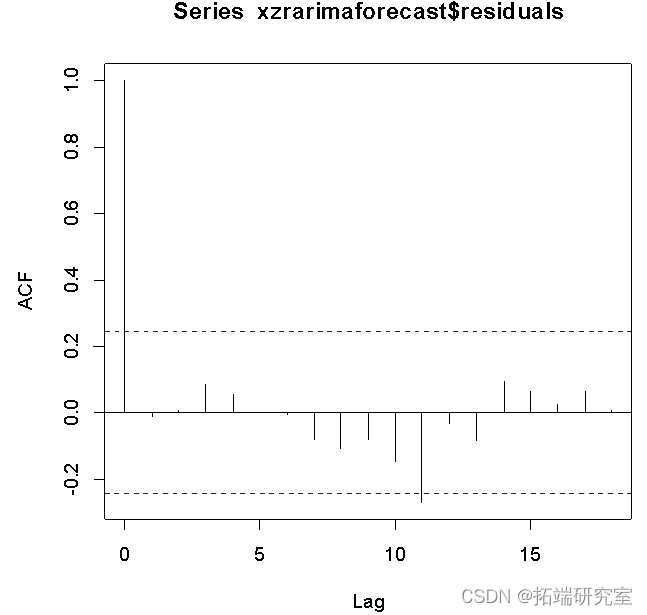
从残差的ACF结果来看,序列很快稳定地落入虚线范围,模型稳定。
plot(Discnt\[,1\],Disnt\[,2\]) points(c(2016:2100) ,Diunt\[66,2\]+diffinv(xzrcast$mean)\[-1\],col="red")#预测值2015到2100年
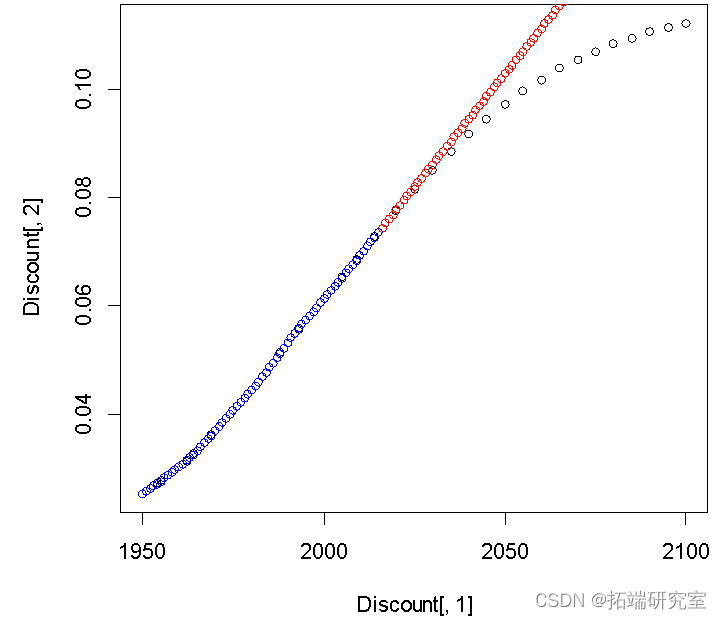
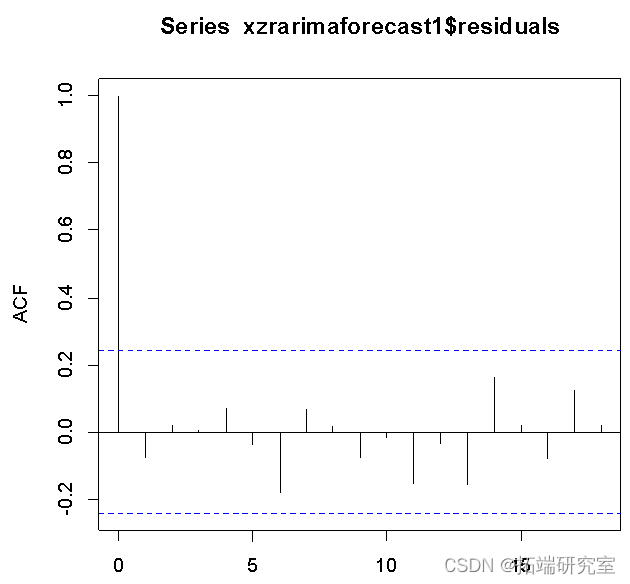
从残差的ACF结果来看,序列很快稳定地落入虚线范围,模型稳定。
为了检验预测误差是均值为零的正态分布,我们可以画出预测误差的直方图,并覆盖上均值为零、标准方差的正态分布的曲线图到预测误差上。
points(mst$mids, myst$density, type="l", col="blue", lwd=2) } plotForecrrors(xzrrecast $residuals)
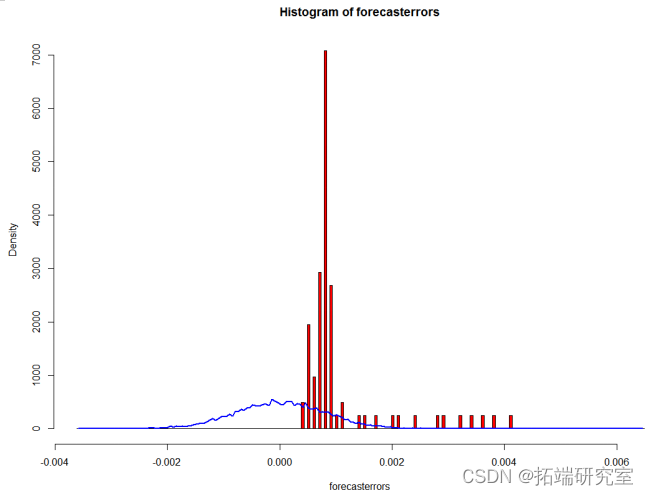
参考文献
【1】统计模拟及其R实现,肖枝洪,武汉大学出版社
【2】Logistic模型在人口预测中的应用,阎慧臻,大连工业大学学报,第27卷第4期
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据
Python+NetworkX+spaCy实现Graph RAG图检索增强生成结合NER与知识图谱优化非结构化文本数据检索|附代码数据 2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载
2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载 中国AI+营销趋势洞察报告2026:生成式AI、代理AI、GEO营销|附400+份报告PDF、数据、可视化模板汇总下载
中国AI+营销趋势洞察报告2026:生成式AI、代理AI、GEO营销|附400+份报告PDF、数据、可视化模板汇总下载 MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据
MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据



