
混合模型在很多方面与线性模型相似。它估计一个或多个解释变量对因变量的影响。
最近我们被客户要求撰写关于混合效应模型的研究报告。混合模型的输出将为解释值列表,它们的效果大小的估计值和置信区间,每种效果的p值以及至少一种模型拟合程度的度量。
可下载资源
当您有一个变量将数据样本描述为可以收集的数据的子集时,应该使用混合模型而不是简单的线性模型。
让我们看一下正在研究的黄蜂亲属识别数据。
str(data)
## 'data.frame': 84 obs. of 6 variables:
## $ Test.ID : int 1 2 3 4 5 6 7 8 9 10 ...
## $ Observer : Factor w/ 4 levels "Charles","Michelle",..: 1 4 2 4 1 3 2 2 1 2 ...
## $ Relation : Factor w/ 2 levels "Same","Stranger": 1 1 1 1 1 1 1 1 1 1 ...
## $ Aggression: int 4 1 15 2 1 0 2 0 3 10 ...
## $ Tolerance : int 4 34 14 31 4 13 7 6 13 15 ...
## $ Season : Factor w/ 2 levels "Early","Late": 1 1 1 1 1 1 1 1 1 1 ...我们已经了解概率的基础,概率中通常将试验的结果称为随机变量。随机变量将每一个可能出现的试验结果赋予了一个数值,包含离散型随机变量和连续型随机变量。
掷硬币就是一个典型的离散型随机变量,离散随机变量可以取无限个但可数的数值。而连续变量相反,它在某一个区间内能取任意的数值。时间就是一个典型的连续变量,1.25分钟、1.251分钟,1.2512分钟,它能无限分割。
既然随机变量可以取不同的值,统计学家就用概率分布描述随机变量取不同值的概率。相对应的,有离散型概率分布和连续型概率分布。
对于离散型随机变量x,定义一个概率函数叫f(x),它给出了随机变量取每一个值的概率。
拿出一个骰子,掷到6的概率是f(6) = 1/6,掷到1和6的概率则是f(1)+f(6) = 1/3。
数学期望和方差
现在有一个运营活动,两套抽奖概率方案,如下:

作为运营人员,应该怎么衡量两种抽奖方法的好坏呢?
数学期望是对随机变量中心位置的一种度量。是试验中每次可能结果的乘以其结果的总和。简单说,它是概率中的平均值,可以用期望对比两套方案。
假设一等奖成本1000元,二等奖成本500元,三等奖成本100元,欢迎下次再来当然没钱,而用户参加一次抽奖需要10元。我们将概率问题转换成运营方的收益和成本计算期望(下面的盈亏是公司角度的)。
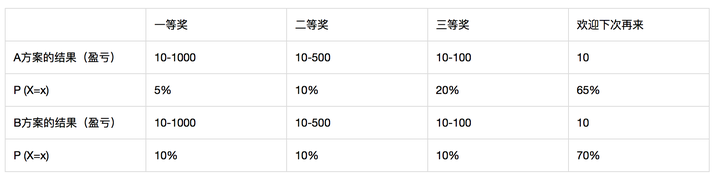
于是E(x) = (-990*5%)+(-490*10%)+(-90*20%)+(10*65%) = -110。也就是说,A方案能够期望每次抽奖运营方亏损110元。计算一下B方案,则是亏损150元。如果从用户的角度看,每一次抽奖的期望则反过来,即一等奖能受益990元,二等奖能受益490元…A方案玩一次平均收益110元。
想必大家已经知道了如何设计活动的盈亏机制,感兴趣可以自行调节中奖概率和成本。
期望值衡量概率的平均值,可是抽奖本来就是很激动人心的事情,哪怕明知道会赔钱,人们还乐此不疲,为什么?因为风险,因为以小搏大。
方差就是这种风险的度量,即随机变量的变异性。它和描述统计学的方差是一个含义。
方差越大,随机变量的结果越不稳定,计算A方案的方差如下:

方差最后为62600,说明期望的波动很大。标准差为sqrt(62600) = 250.19,代表每一次的抽奖,与期望收益-110的距离是250.19元。
到这里,概率和期望方差的基本玩法已经讲完了。
二项概率分布
二项分布是一种离散型的概率分布。故明思义,二项代表它有两种可能的结果,把一种称为成功,另外一种称为失败。
除了结果的规定,它还需要满足其他性质:每次试验成功的概率均是相同的,记录为p;失败的概率也相同,为1-p。每次试验必须相互独立,该试验也叫做伯努利试验,重复n次即二项概率。
掷硬币就是一个典型的二项分布。当我们要计算抛硬币n次,恰巧有x次正面朝上的概率,可以使用二项分布的公式:
假设抛硬币5次,恰巧有3次正面朝上,则其概率为31.25%。可以使用Excel中的BINOM.DIST函数计算。
不妨把题目变化一下,变成计算硬币至少有三次正面朝上的概率是多少?有一种简单的方法是累加,将恰巧有3次,恰巧有4次,恰巧有5次的概率相加,结果便是至少3次,为50%。
回到运营活动的例子,上面一个运营活动公司亏惨了,现在运营需要重新做一个抽奖活动,每位用户拥有10次抽奖机会,中奖概率是5%。老板准备先考虑成本问题,想知道至少有3次以上中奖机会的概率是多少?
按照上题的思路,可以拿恰巧3次,恰巧4次直到恰巧10次累加求和,但是这样太麻烦了。此时可以换一个思路,先计算最多2次的概率是多少。那么便是f(0)+f(1)+f(2),结果是92.98%,利用概率公式1-92.98%,就是至少3次的概率了,为7.02%。看来老板还是能松口气的。
二项概率的数学期望为E(x) = np,方差Var(x) = np(1-p)。抽奖10次,那么抽奖的期望值就是0.5,方差为0.%*0.95。
运营学会二项分布,在涉及概率的各种活动中,将变得游刃有余。它的原理甚至能用到AB测试。大学考试中二项概率需要查专门的概率表计算,不过现在各类工具层出不穷,Python、R、Excel都能直接计算。
泊松概率分布
泊松概率是另外一个常用的离散型随机变量,它主要用于估计某事件在特定时间或空间中发生的次数。比如一天内中奖的个数,一个月内某机器损坏的次数等。
泊松概率的成立条件是在任意两个长度相等的区间中,时间发生的概率是相同的,并且事件是否发生都是相互独立的。
泊松概率既然表示事件在一个区间发生的次数,这里的次数就不会有上限,x取值可以无限大,只是可能性无限接近0,f(x)的最终值很小。
x代表发生x次,u代表发生次数的数学期望,概率函数为:
现在又举办了一个新的运营活动,这次的中奖概率未知,只知24小时内中奖的平均个数为5个,老板异想天开地想知道24小时内恰巧中奖次数为7的概率是多少?
此时x=7,u=5(区间内发生的平均次数就是期望),代入公式求出概率为10.44%。Excel中的函数为POISSON.DIST。
接下来继续加大问题难度,求中奖次数至少7次的概率。此时f(0)+f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=86.66%,那么至少七次的概率为13.33%。
如果问题变成12小时内呢?老板希望知道12小时内中奖次数为3次的概率是多少?
24小时内中奖概率的期望数是5,那么12小时内的中奖概率期望数是2.5,于是令u=2.5,求出12小时内中奖次数为3的概率是79.99%。
泊松概率还有一个重要性质,它的数学期望和方差相等,所以上题的方差为2.5,标准差为根号2.5,即1.58。
正态分布
上述分布都是离散概率分布,当随机变量是连续型时,情况就完全不一样了。因为离散概率的本质是求x取某个特定值的概率,而连续随机变量不行,它的取值是可以无限分割的,它取某个值时概率近似于0。连续变量是随机变量在某个区间内取值的概率,此时的概率函数叫做概率密度函数。
正态概率分布是连续型随机变量中最重要的分布。世界上绝大部分的分布都属于正态分布,人的身高体重、考试成绩、降雨量等都近似服从。
正态分布如同一条钟形曲线。中间高,两边低,左右对称。想象身高体重、考试成绩,是否都呈现这一类分布态势:大部分数据集中在某处,小部分往两端倾斜。
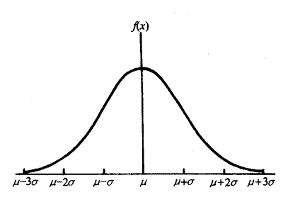
正态概率密度函数为:
是不是看得头晕了?u代表均值,σ代表标准差,两者不同的取值将会造成不同形状的正态分布。均值表示正态分布的左右偏移,标准差决定曲线的宽度和平坦,标准差越大曲线越平坦。
以前介绍过一个正态分布的经验法则:
正态随机变量有69.3%的值在均值加减一个标准差的范围内,95.4%的值在两个标准差内,99.7%的值在三个标准差内。这条经验法则可以帮助我们快速计算数据的大体分布。
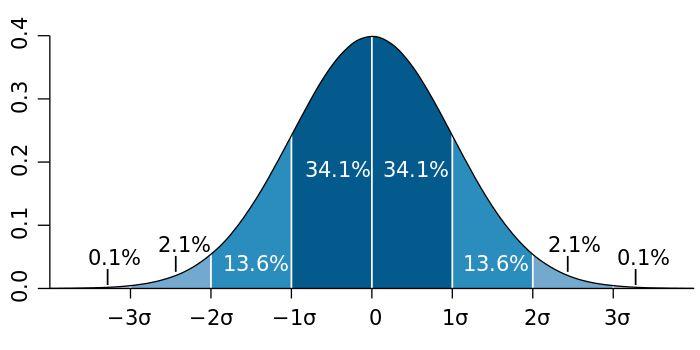
均值u=0,标准差σ=1的正态分布叫做标准正态分布。它的随机变量用z表示,它是推断统计的基础。将均值和标准差代入正态概率密度函数,得到一个简化的公式:
现在可以用简化的公式计算概率密度了。首先学习一个新的函数叫累计分布函数,它是概率密度函数的积分。用P(X<=x)表示随机变量小于或者等于某个数值的概率,F(x) = P(X<=x)。
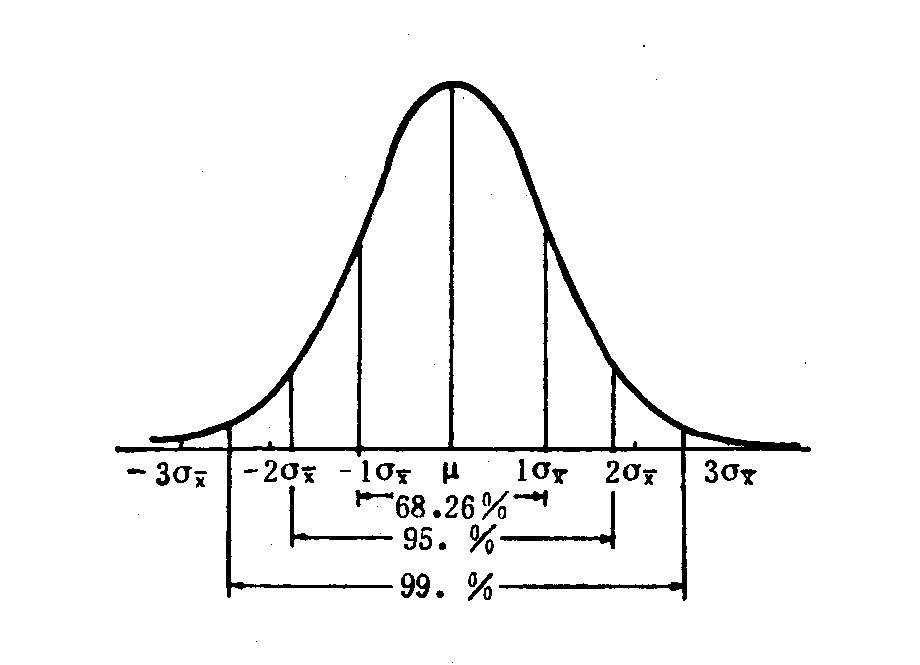
标准正态分布中,给定一个值z,可以计算随机变量z小于等于某一个值的概率;z在两个值之间的概率;以及z大于等于一个值的概率。这三种计算都用到累计分布函数,分别记作P(z<=x),P(x1<=z<=x2),P(z>=x)。
首先计算z小于等于1的概率,即P(z<=1)。由excel 的函数NORM.DIST(1,0,1,TRUE)求得值为0.8413。于是P(z<=1)=0.8413。同理,P(z>1) = 1-P(z<=1) = 0.1586。
若要计算z在区间-1~1.25的概率,即P(-1<=z<=1.25)。可以将其拆解为公式:P(-1<=z<=1.25) = P(z<=1.25) – P(z<=-1) = 0.735。
如果大家在公式转换中有困惑,不妨结合上面的阴影图看。靠左的阴影即z小于等于0.8时(目测)的概率,如果我们要算0~0.8之间的概率呢?就是把z<=0的那一半给挖掉,非常粗暴的算法。
到了这里大家可能发觉,在正态分布的计算中,不论求哪一类区间,我们都是先转换成z小于等于某个值先计算。这是一个潜移默化的规则,因为早期正态概率的计算都要用到标准正态概率表,它以z小于等于作查询标准。现在虽然计算资源已经大大丰富,但是这个习惯还是保留了下来。
之所以强调标准正态分布,是因为所有的正态分布概率都可以利用标准正态分布计算。当我们具有一个任意均值的u和标准差σ,都能将其转换成标准状态分布。
现在有一个u=10和σ=2的正态随机变量,求x在10与14之间的概率是多少?
当x=10时,z=(10-10)/2=2。当x=14时,z=(14-10)/2=2。于是x在10和14之间的概率等价于标准正态分布中0和2之间的概率。计算P(0<=z<=2) =P(z<=2) – P(z<=0) =0.4772。
现在是最后一个运营活动了,不再是抽奖,而是最终赠送奖品的环节。已知奖品的保质期满足正态分布,均值90天,标准差5天。为了考虑用户体验,想知道奖品70天以内就坏的概率是多少?
当x=70时,有z=(70-90)/5 = -4。p(z<=-4)=0.003%。概率非常小,可以忽略不计,所以产品质量杠杠的。经历了那么多活动,老板终于可以松一口气了。
在概率分布中还有一个概念叫正态近似。当试验次数很大时,二项分布可以近似于正态分布,泊松分布也有相似的情况,大家有兴趣可以去了解,这是一种简便方法,不过工作中现在都是计算机了,这点反而不重要了。
我感兴趣的因变量是攻击性和宽容度。侵略性是指六十分钟内的攻击行为次数。宽容是指六十分钟内的宽容行为数量。我对关系(无论黄蜂来自相同还是不同的菌落)和季节(菌落周期的早期或晚期)对这些因变量的影响感兴趣。这些影响是“固定的”,因为无论我在何处,如何采样或采样了多少只黄蜂,我在相同变量中仍将具有相同的水平:相同的菌落与不同的菌落,以及早季与晚季。
但是,还有两个其他变量在样本之间不会保持固定。如果我在不同的年份进行采样,那么观察者的水平会有所不同。样品之间的测试ID也会有所不同,因为我总是可以重新安排哪些黄蜂参与每个实验试验。每个试验都是我当时收集的黄蜂的唯一子样本。如果我能够单独测试黄蜂,并且如果所有观察都对所有互动进行了评分,那么我将不会有任何随机效应。但是,相反,我的数据本来就是“块状”的,随机效应描述了这种块状性。
在继续之前,您还需要考虑随机效果的结构。您的随机效果是嵌套还是交叉?在我的研究中,随机效应是 嵌套的,因为每个观察者记录了一定数量的试,并且没有两个观察者记录了相同的试验,因此Test.ID嵌套在Observer中。但是说我收集了五个不同遗传谱系中的黄蜂。“遗传学”的随机效应与观察无关。它将与其他两个随机效应交叉。因此,这种随机效应将 与其他效应 交叉。
2.哪种概率分布最适合您的数据?
假设您已决定要运行混合模型。接下来要做的是找到最适合您数据的概率分布。有很多测试方法。请注意,负二项式和伽马分布只能处理正数,而泊松分布只能处理正整数。二项分布和泊松分布与其他分布不同,因为它们是离散的而不是连续的,这意味着它们可以量化不同的,可数的事件或这些事件的概率。现在让我们为我的Aggression变量找到一个合适的分布。
require(car)
## 正在加载所需的包: car
require(MASS)
# 必须为非零的分布
qqp(Aggression, "norm")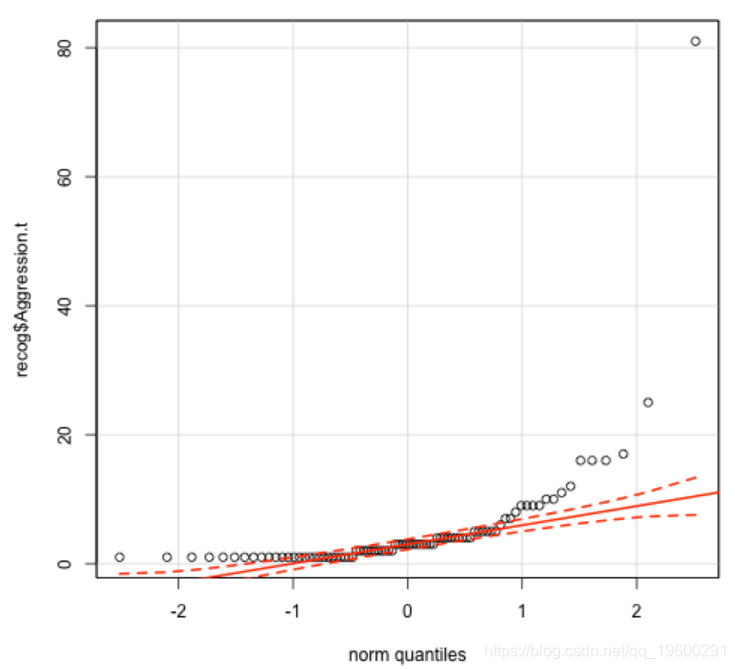
# lnorm 表示对数正态
qqp(Aggression, "lnorm")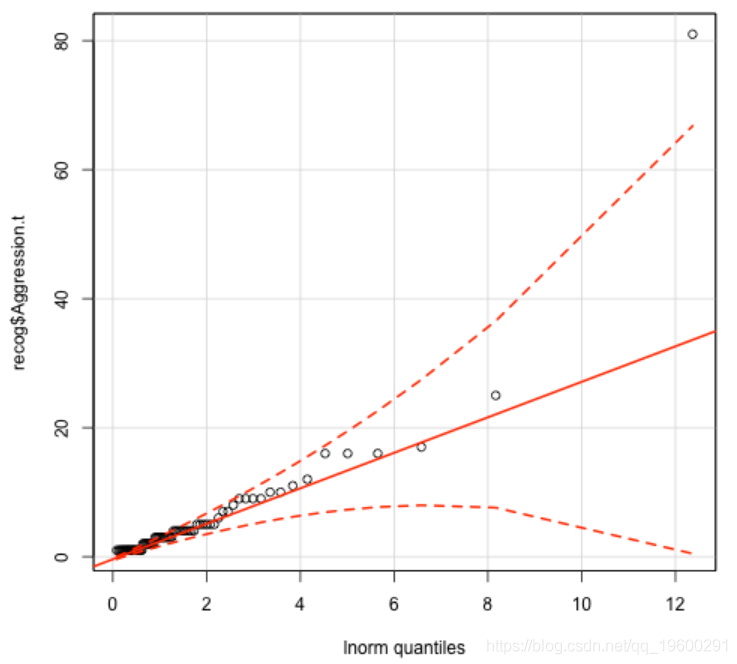
# qqp需要估计负二项式,泊松和伽玛分布的参数。您可以使用fitdistr函数生成估算值。保存输出并提取每个参数的估计值,如下所示。
fitdistr(rAggression, "Negative Binomial")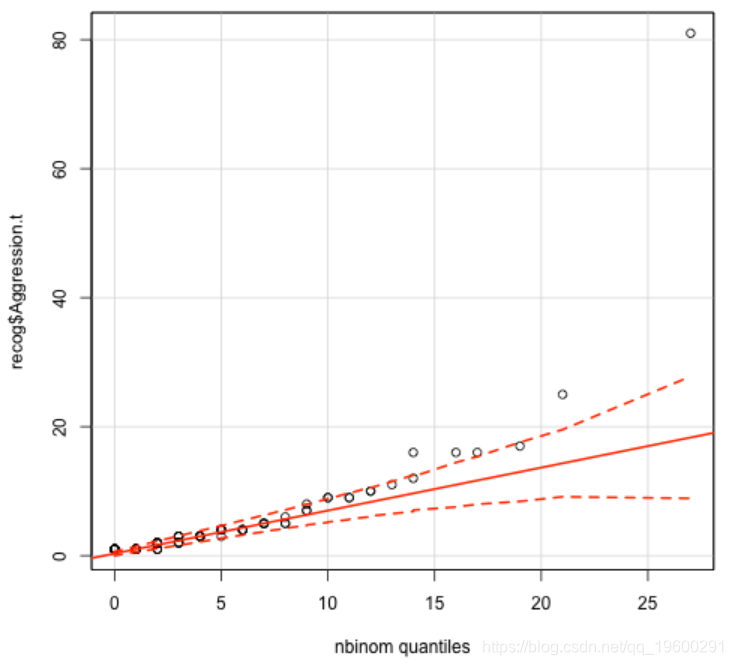
qqp(Aggressio, "pois", estimate)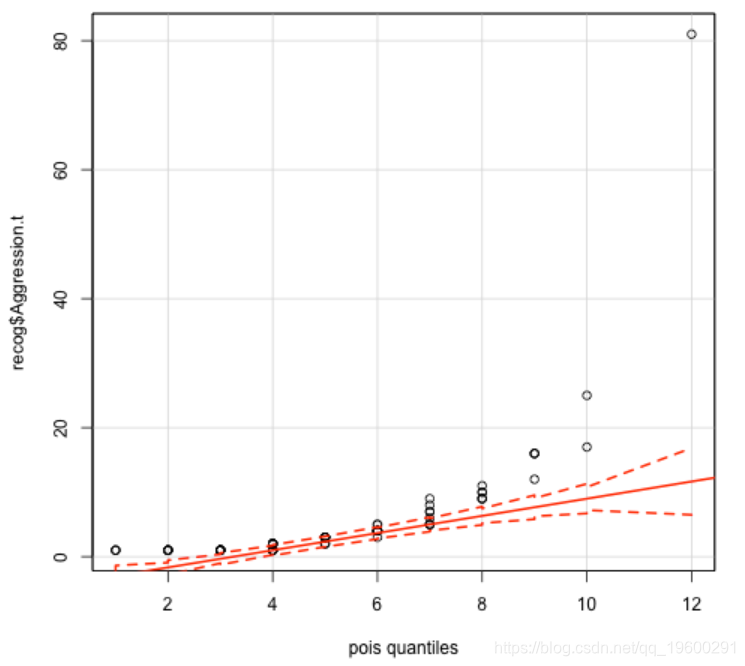
绘图对评估模型拟合也很重要。通过以各种方式绘制拟合值,您可以确定哪种模型适合描述数据。
fitdistr(Aggression.t, "gamma")

查看我使用qqp生成的图。y轴表示观测值,x轴表示通过分布建模的分位数。红色实线表示理想分布拟合,红色虚线表示理想分布拟合的置信区间。您想选择最大的观测值落在虚线之间的分布。在这种情况下,这就是对数正态分布,其中只有一个观测值落在虚线之外。现在,我可以尝试拟合模型。
3.如何将混合模型拟合到您的数据
3a.如果您的数据是正态分布的
首先,请注意:如果您的数据最适合对数正态分布, 请不要对其进行变换。 由于变换使模型结果的解释更加困难。
如果数据呈正态分布,则可以使用线性混合模型(LMM)。该函数的第一个参数是一个公式,形式为y〜x1 + x2 …等,其中y是因变量,而x1,x2等是解释变量。交叉随机效应的形式为(1 | r1)+(1 | r2)…,而嵌套随机效应的形式为(1 | r1 / r2)。
在这里,您可以指定混合模型将使用最大似然还是受限最大似然来估计参数。如果您的随机效应是嵌套的,或者只有一个随机效应,并且您的数据是平衡的(即,每个因子组中的样本量相似),则将REML设置为FALSE,因为您可以使用最大似然率。如果交叉了随机效果,请不要设置REML参数,因为无论如何它默认为TRUE。
为了避免这一切看起来太抽象,让我们尝试一些数据。我们将有关八哥歌曲研究的一些数据。
在这项研究中,我们对雄性和雌性八哥歌曲之间的差异以及社会地位,不同的鸟类的歌唱是否不同感兴趣。我们的随机效应是社会群体。歌曲的平均音高符合正态概率分布。
str(starlings)
## 'data.frame': 28 obs. of 5 variables:
## $ Individual : Factor w/ 28 levels "B-40917","B-41205",..: 4 5 6 15 3 16 8 13 20 14 ...
## $ Sex : Factor w/ 2 levels "F","M": 2 2 2 2 2 1 1 1 1 2 ...
## $ Group : Factor w/ 5 levels "DRT1","MRC1",..: 2 5 5 4 4 4 4 4 4 4 ...
## $ Social.Rank: Factor w/ 2 levels "Breeder","Helper": 2 1 1 1 2 2 2 2 1 2 ...
## $ Mean.Pitch : num 2911 2978 3313 3268 3312 ...
summary(lmm)
## Linear mixed model fit by maximum likelihood ['lmerMod']
## Formula: Mean.Pitch ~ Sex + Social.Rank + (1 | Group)
## Data: starlings
##
## AIC BIC logLik deviance df.resid
## 389.3 396.0 -189.7 379.3 23
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.0559 -0.6272 0.0402 0.5801 2.0110
##
## Random effects:
## Groups Name Variance Std.Dev.
## Group (Intercept) 0 0
## Residual 44804 212
## Number of obs: 28, groups: Group, 5
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 3099.0 82.2 37.7
## SexM 51.7 81.3 0.6
## Social.RankHelper -45.0 82.4 -0.5
##
## Correlation of Fixed Effects:
## (Intr) SexM
## SexM -0.630
## Scl.RnkHlpr -0.668 0.106让我们看看结果。首先,我们获得一些模型拟合的度量,包括AIC,BIC,对数似然度和偏差。然后我们得到由随机效应解释的方差估计。这个数字很重要,因为如果它与零没有区别,那么您的随机效应可能并不重要,您可以继续进行常规的线性模型建立。接下来,我们将对固定效应进行估算,带有标准误差。这些信息可能足以满足您的需求。一些期刊将这些模型的结果报告为带有置信区间的效应大小。当然,当我查看固定效应估算值时,我已经可以看出,性别和社会地位之间的平均音高没有差异。但是有些期刊希望您报告p值。
如果您想要一些p值,则需要使用Anova函数。
## Analysis of Deviance Table (Type II Wald chisquare tests)
##
## Response: Mean.Pitch
## Chisq Df Pr(>Chisq)
## Sex 0.4 1 0.52
## Social.Rank 0.3 1 0.58Anova函数进行了Wald检验,该检验告诉我们我们对性别和社会地位对音高的影响的估计p值。
拟合线性混合模型时,可能会遇到一种复杂情况。R可能会有“无法收敛”错误,通常将其表述为“没有收敛就达到了迭代限制”。这意味着您的模型有太多因素,样本量不够大,无法拟合。然后,您应该做的是从模型中删除固定效果和随机效果,然后进行比较以找出最合适的效果。一次删除固定效果和随机效果。保持固定效果不变,并一次删除一个随机效果,然后找出最合适的效果。然后保持随机效果不变,并一次删除固定效果。在这里,我只有一种随机效果,
anova(noranklmm, nosexlmm, nofixedlmm)
## Data: starlings
## Models:
## nofixedlmm: Mean.Pitch ~ 1 + (1 | Group)
## noranklmm: Mean.Pitch ~ Sex + (1 | Group)
## nosexlmm: Mean.Pitch ~ Social.Rank + (1 | Group)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## nofixedlmm 3 386 390 -190 380
## noranklmm 4 388 393 -190 380 0.48 1 0.49
## nosexlmm 4 388 393 -190 380 0.00 0 1.00请注意,该方差分析函数与我们用来评估模型中固定效果的重要性的方差分析函数不同。方差分析函数用于比较模型。p值表明模型之间没有明显的重要差异。我们还可以比较AIC值,请注意,具有最低AIC值的模型是完全没有固定影响的模型,这符合我们的理解,即性别和社会地位对歌曲的音调没有影响。无论采用哪种方法,请务必在稿件中报告用于选择最佳模型的p值或AIC值。
随时关注您喜欢的主题
3b.如果您的数据不是正态分布的
您会看到,用于估计模型中影响大小的REML和最大似然法做出了不适用于数据的正态假设,因此您必须使用其他方法进行参数估计。问题在于,存在许多替代的估算方法,每种估算方法都使用不同的R包运行,并且很难确定哪种方法合适。
首先,我们需要测试是否可以使用惩罚拟似然(PQL)。PQL是一种灵活的技术,可以处理非正常数据,不平衡设计和交叉随机效应。但是,如果您的因变量符合离散计数分布(例如泊松或二项式)且均值小于5,或者您的因变量为二元变量,则会产生偏差估计。
Aggression变量适合对数正态分布,该分布不是离散分布。这意味着我们可以继续使用PQL方法。但是在继续之前,让我们回到转变为正态的问题。
将分布设置为对数正态,我们将族设置为高斯,并将链接设置为log。
## lmList
summary(PQL)
## Linear mixed-effects model fit by maximum likelihood
## Data: recog
## AIC BIC logLik
## NA NA NA
##
## Random effects:
## Formula: ~1 | Observer
## (Intercept)
## StdDev: 0.3312
##
## Formula: ~1 | Test.ID %in% Observer
## (Intercept) Residual
## StdDev: 0.5295 7.128
##
## Variance function:
## Structure: fixed weights
## Formula: ~invwt
## Fixed effects: Aggression.t ~ Relation + Season
## Value Std.Error DF t-value p-value
## (Intercept) 1.033 0.5233 55 1.974 0.0535
## RelationStranger 1.210 0.4674 55 2.589 0.0123
## SeasonLate -1.333 0.5983 23 -2.228 0.0359
## Correlation:
## (Intr) RltnSt
## RelationStranger -0.855
## SeasonLate -0.123 0.000
##
## Standardized Within-Group Residuals:
## Min Q1 Med Q3 Max
## -4.86916 -0.29958 -0.08012 0.14280 5.93336
##
## Number of Observations: 84
## Number of Groups:
## Observer Test.ID %in% Observer
## 4 28该模型表明季节对侵略性有影响,也就是说,在菌落周期后期收集的黄蜂比早期收集的黄蜂侵略性小。这也表明黄蜂之间的关系有影响。他们相对于巢友更可能对陌生人有侵略性。我将这些统计数据与估计值,标准误,t值和p值一起报告。
那么,如果您的因变量的平均值小于5,或者您有一个二元因变量,而您不能使用PQL,该怎么办?在这里,您可以使用两种选择:拉普拉斯(Laplace)近似 和马尔可夫链蒙特卡罗算法(MCMC)。拉普拉斯近似值最多可以处理3个随机效果。除此之外,您还必须使用MCMC。
让我们从一个可以使用拉普拉斯逼近的例子开始。我们将使用学生在学校的学习情况的数据。出于本示例的目的,我将仅将数据子集化为几个感兴趣的变量,并将“ repeatgr”变量简化为二元因变量。
str(bdf)
## 'data.frame': 2287 obs. of 4 variables:
## $ schoolNR: Factor w/ 131 levels "1","2","10","12",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ Minority: Factor w/ 2 levels "N","Y": 1 2 1 1 1 2 2 1 2 2 ...
## $ ses : num 23 10 15 23 10 10 23 10 13 15 ...
## $ repeatgr: Factor w/ 3 levels "0","1","2": 1 1 1 1 1 1 1 1 2 1 ...严格来说,Laplace近似 是一种称为Gauss-Hermite正交(GHQ)的参数估算方法的特例,需要进行一次迭代。
假设我们要找出是否属于少数民族和社会经济地位会影响学生复读成绩的可能性。我们的因变量是“ repeatgr”,指示学生是否重复了成绩。少数族身份是二元Y / N类别,社会经济地位由“ ses”表示,其数字范围为10至50,其中50是最富有的。我们的随机因素是“ schoolNR”,它代表从中采样学生的学校。因为因变量是二元的,所以我们需要具有二项式分布的广义线性混合模型,并且由于我们的随机效应少于五个,因此可以使用Laplace近似 。
GHQ由于重复迭代而比Laplace更为准确,但在第一次迭代后变得不那么灵活,因此您只能将它用于一个随机效果。我们唯一的随机效应是“ schoolNR”。
summary(GHQ)
## Generalized linear mixed model fit by maximum likelihood (Adaptive
## Gauss-Hermite Quadrature, nAGQ = 25) [glmerMod]
## Family: binomial ( logit )
## Formula: repeatgr ~ Minority + ses + ses * Minority + (1 | schoolNR)
## Data: bdf
##
## AIC BIC logLik deviance df.resid
## 1672.8 1701.4 -831.4 1662.8 2282
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -0.964 -0.407 -0.314 -0.221 5.962
##
## Random effects:
## Groups Name Variance Std.Dev.
## schoolNR (Intercept) 0.264 0.514
## Number of obs: 2287, groups: schoolNR, 131
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.45194 0.20763 -2.18 0.03 *
## MinorityY 0.47957 0.47345 1.01 0.31
## ses -0.06205 0.00798 -7.78 7.5e-15 ***
## MinorityY:ses 0.01196 0.02289 0.52 0.60
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) MnrtyY ses
## MinorityY -0.400
## ses -0.905 0.369
## MinortyY:ss 0.299 -0.866 -0.321
Laplace <- glmer(repeatgr ~ Minority + ses + ses * Minority + (1 | schoolNR),
data = bdf, family = binomial(link = "logit")) # Contrast to the Laplace approximation
## Warning: Model failed to converge with max|grad| = 0.0458484 (tol = 0.001)
summary(Laplace)
## Generalized linear mixed model fit by maximum likelihood (Laplace
## Approximation) [glmerMod]
## Family: binomial ( logit )
## Formula: repeatgr ~ Minority + ses + ses * Minority + (1 | schoolNR)
## Data: bdf
##
## AIC BIC logLik deviance df.resid
## 1672.8 1701.5 -831.4 1662.8 2282
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -0.960 -0.407 -0.316 -0.222 5.950
##
## Random effects:
## Groups Name Variance Std.Dev.
## schoolNR (Intercept) 0.258 0.508
## Number of obs: 2287, groups: schoolNR, 131
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.45456 0.20611 -2.21 0.027 *
## MinorityY 0.48005 0.47121 1.02 0.308
## ses -0.06191 0.00791 -7.83 4.9e-15 ***
## MinorityY:ses 0.01194 0.02274 0.53 0.600
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr) MnrtyY ses
## MinorityY -0.400
## ses -0.906 0.369
## MinortyY:ss 0.299 -0.866 -0.321您可以看到在这种情况下,Laplace和GHQ之间没有重要区别。两者都表明,社会经济课对学生复读成绩的可能性有非常显着的影响,尽管即使采用logit变换,我们也可以看到影响量很小。但是,使用此方法时,还需要考虑其他一些因素。当用于过度分散的数据时,即合并的残差远大于残差自由度时,它变得不准确。使用此方法时,应检查模型以确保数据不会过度分散。
## n×n方差-协方差矩阵中方差参数的数量
vpars <- function(m) {
nrow(m) * (nrow(m) + 1)/2
}
# 接下来计算剩余自由度
rdf <- nrow(model.frame(model)) - model.df
# 提取皮尔逊残差
prat <- Pearson.chisq/rdf
# 生成一个p值。如果小于0.05,则数据过于分散。
这些学校数据并不分散。如果是,可以将过度分散建模为随机效应,每个观察值具有一个随机效应水平。在这种情况下,我将使用学生ID作为随机效果变量。
考虑有关大麦农民的这些数据。想象一下,要使大麦收成产生利润,大麦收成的收入必须大于140。
farmers <- farmers[c(1:5, 8)]
str(farmers)
## 'data.frame': 102 obs. of 6 variables:
## $ year : int 1901 1901 1901 1901 1902 1902 1902 1902 1902 1902 ...
## $ farmer : Factor w/ 18 levels "Allardyce","Dooley",..: 10 5 3 18 10 5 18 17 4 12 ...
## $ place : Factor w/ 16 levels "Arnestown","Bagnalstown",..: 3 16 14 11 3 16 11 4 8 6 ...
## $ district: Factor w/ 4 levels "CentralPlain",..: 2 2 1 1 2 2 1 1 4 4 ...
## $ gen : Factor w/ 2 levels "Archer","Goldthorpe": 1 1 1 1 1 1 1 1 1 1 ...
## $ profit : num 1 1 1 1 1 1 1 1 1 1 ...我们继续讨论泊松数据的均值太小或因变量是分类的情况,并且我们有五个或五个以上随机效应。
在这种情况下,假设我们根本没有解释变量。我们对哪些随机效应会影响利润感兴趣。毕竟,随机效应是改变因变量方差的因素。为此,我们将处理随机效应,而且还为随机效应提供置信区间。
所有模型都对数据中方差的分布进行假设,但是在贝叶斯方法中,这些假设是明确的,因此我们需要指定这些假设的分布。在贝叶斯统计中,我们称这些 先验。
## Iterations = 3001:12991
## Thinning interval = 10
## Sample size = 1000
##
## DIC: 76.61
##
## G-structure: ~year
##
## post.mean l-95% CI u-95% CI eff.samp
## year 18.2 0.266 68.6 18.1
##
## ~farmer
##
## post.mean l-95% CI u-95% CI eff.samp
## farmer 1.93 0.0789 6.68 99.7
##
## ~place
##
## post.mean l-95% CI u-95% CI eff.samp
## place 1.54 0.0711 4.84 173
##
## ~gen
##
## post.mean l-95% CI u-95% CI eff.samp
## gen 12.1 0.0874 28.6 1000
##
## ~district
##
## post.mean l-95% CI u-95% CI eff.samp
## district 1.78 0.0639 5.63 1000
##
## R-structure: ~units
##
## post.mean l-95% CI u-95% CI eff.samp
## units 1 1 1 0
##
## Location effects: profit ~ 1
##
## post.mean l-95% CI u-95% CI eff.samp pMCMC
## (Intercept) 3.47 -1.16 10.75 220 0.14如果我们看一下均值和置信区间,我们可以看到,真正影响利润可变性的唯一随机效应是年份和基因型。也就是说,大麦收成获利的可能性每年之间以及基因型之间变化很大,但是在农民或地方之间变化不大。
结束:了解您的数据
除非您熟悉这些分析,否则您将无法真正知道哪种分析对您的数据适用,而熟悉它们的最佳方法是绘制它们。通常,我的第一步是绘制我感兴趣的变量的密度图。
ggplot(recog, aes(x = Aggression)+ geom_density() +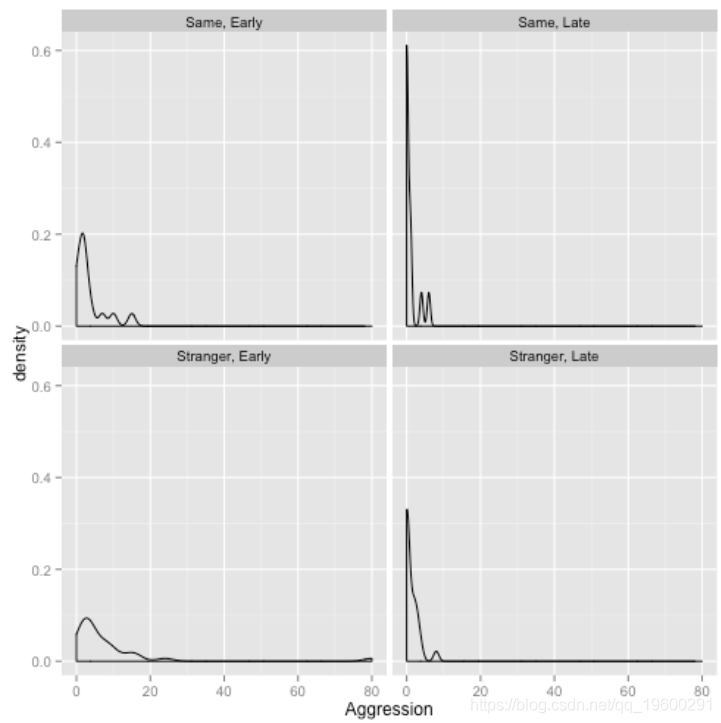
在这里,我按季节和关系(两个固定效应)划分了数据。我们可以立即看到数据集包含一个极端正的异常值;大多数观测值都介于0到20之间。我们还可以看到,后期观测值的很大一部分等于零。
绘图对于评估模型拟合也很重要。您可以通过各种方式绘制拟合值来判断适合的模型最能描述数据。一个简单的应用是绘制模型的残差。如果您将模型想象为通过数据散点图的最佳拟合线,则残差为散点图中各点与最佳拟合线之间的距离。如果模型适合,则将残差与拟合值作图,则应该看到随机散布。如果散布不是随机的,则意味着还有其他随机或固定的影响。
让我们尝试绘制拟合八哥的歌曲音高的混合模型的残差。此图所做的是创建一条表示零的水平虚线:与最佳拟合线的零偏差平均值。它还创建了一条实线,代表与最佳拟合线的残差。我希望实线覆盖虚线。
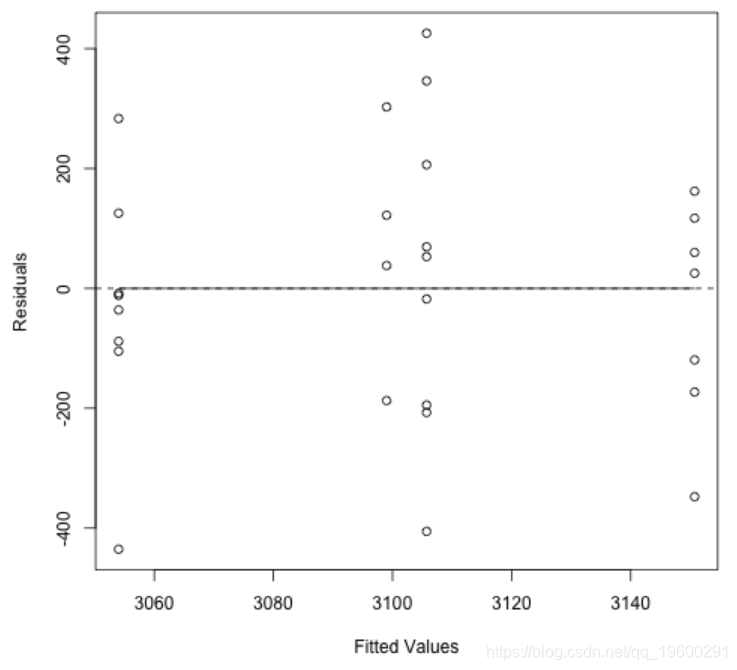
结果很好:与最佳拟合线的偏差趋于零。
让我们尝试一种以图形方式比较MCMC模型的技术。我们将回到大麦农户的示例。
Trace(MCMC, log = TRUE)
这些随机效果看起来不像白噪声。因此,让我们尝试使用更多迭代来重新拟合模型。这需要更多的计算量,但会产生更准确的结果。
Trace(MCMC2, log = TRUE)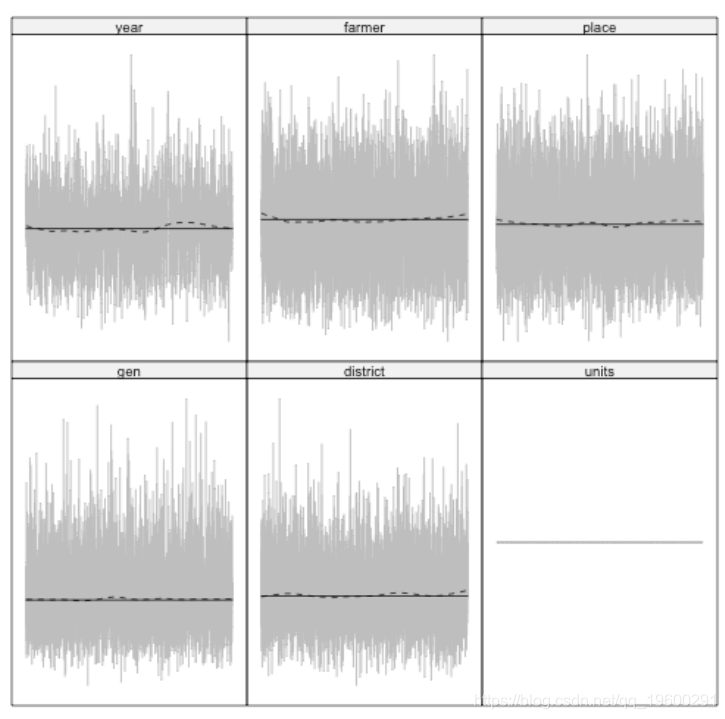
现在,看起来都更接近直线周围的白噪声,这表明模型更好。现在,让我们比较两个模型之间随机效应方差的置信区间。
# 将两个模型的估计值和置信区间放在一起
rbind (covariances, Gcovariances)
# 创建一个数据框架,其中包含模型和随机效应的因素
data.frame(coint, model = factor(el1", "model2"), eac),
random.effect = dimnames(i)
## Warning: some row.names duplicated: 6,7,8,9,10 --> row.names NOT used
# 将估计和置信区间绘制为按模型分组的箱形图
ggplot(conf.int+ geom_crossbar(aes(y.95..CI,
y.95..CI= model= "dodge")
结果很好,因为两个模型之间的估算值非常相似,但是在第二个模型中,对年的置信区间明显较小,说明这个估计更好。图中可以证明第二种模型的推论,即基因型和年份是变异的主要因素。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 R语言非参数回归预测摩托车事故、收入数据:局部回归、核回归、LOESS可视化
R语言非参数回归预测摩托车事故、收入数据:局部回归、核回归、LOESS可视化 【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现 Python个人收入影响因素模型构建:回归、决策树、梯度提升、岭回归
Python个人收入影响因素模型构建:回归、决策树、梯度提升、岭回归 【视频讲解】滚动回归Rolling Regression、ARIMAX时间序列预测Python、R实现应用
【视频讲解】滚动回归Rolling Regression、ARIMAX时间序列预测Python、R实现应用


