
诸如核密度估计(KDE)的平滑方法被用于控制用于计算每种疾病率的空间支持的群体基础。
平滑程度由用户定义的参数(带宽或阈值)控制,该参数影响疾病图的分辨率和计算的速率的可靠性。
可下载资源
方法
内核,带宽的大小,是影响在KDE [在地图上的平滑的程度的关键参数 ]。带宽可以是固定的也可以是可变的(自适应的)。对于固定带宽方法,内核具有固定大小的半径,并且所有内核(圆圈)具有相同的半径。在健康研究中,固定带宽方法可能不合适,因为人口不是均匀分布在地理空间中。此外,如果圆圈落入低人口密度区域,可能会导致不稳定的比率。类似地,在自适应带宽方法中,内核半径增大或缩小以适应不同的种群大小。用于定义内核带宽的最小种群大小,以及因此地图上的平滑程度,是用户定义的参数。我们将其称为阈值(h)。
核密度估计其实是对直方图的一个自然拓展。
首先考虑一下密度函数的概念,很自然的可以想到,密度函数就是分布函数的一阶导数。那么当我们拿到一些数据的时候,是不是可以通过估计分布函数的一阶导数来估计密度函数呢?一个最简单而有效的估计分布函数的方法是所谓的「经验分布函数(empirical distribution function)」:
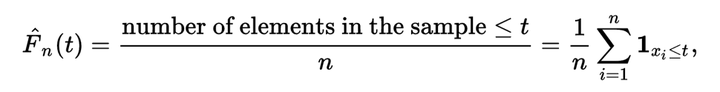
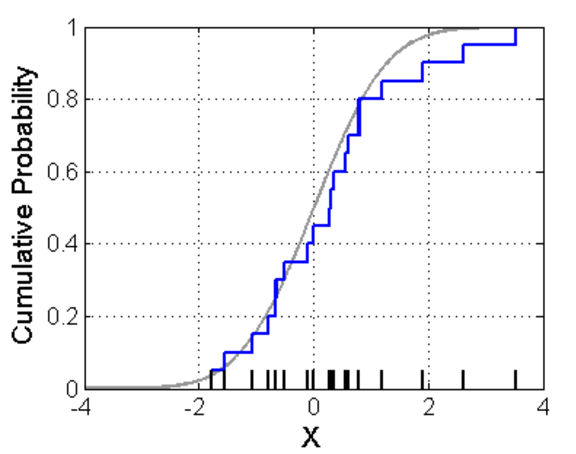
可是这个EDF不是可导的,不够光滑,因而不能通过对EDF的一阶导数算密度函数。那么如何估计密度函数呢?
我们一般看密度的时候,会首先画一个直方图,像下图:
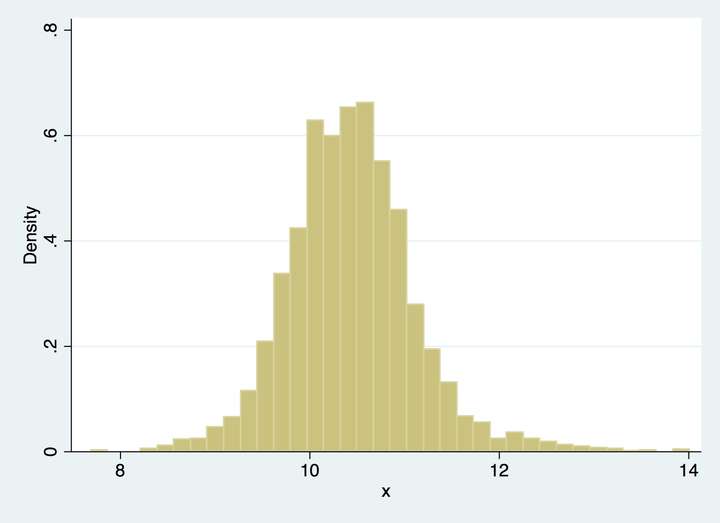
一个很自然的想法是,如果我们想知道X=x处的密度函数值,可以像直方图一样,选一个x附近的小区间,数一下在这个区间里面的点的个数,除以总个数,应该是一个比较好的估计。用数学语言来描述,如果你还记得导数的定义,密度函数可以写为:
我们把分布函数用上面的经验分布函数替代,那么上式分子上就是落在[x-h,x+h]区间的点的个数。我们可以把f(x)的估计写成:
那么一个很自然的问题来了,h该怎么选取呢?
给定样本容量N,h如果选的太大,肯定不符合h趋向于0的要求。h选的太小,那么用于估计f(x)的点实际上非常少。
这也就是非参数估计里面的bias-variance tradeoff:如果h太大,用于计算的点很多,可以减小方差,但是方法本质要求h→0,bias可能会比较大;如果h太小,bais小了,但是用于计算的点太少,方差又很大。
所以理论上存在一个最小化mean square error的一个h。h的选取应该取决于N,当N越大的时候,我们可以用一个比较小的h,因为较大的N保证了即使比较小的h也足以保证区间内有足够多的点用于计算概率密度。因而,我们通常要求当N→∞,h→0。比如,在这里可以推导出,最优的h应该是N的-1/5次方乘以一个常数,也就是。对于正态分布而言,可以计算出c=1.05×标准差。
另外,我们知道之前的经验分布函数每个点的收敛速度都是√N的,而这里,因为有h的存在(观察估计式,分母上是nh而非n,而nh=O(N^{-4/5}))。所以收敛速度比一般的参数收敛速度要慢很多。
上面的这个估计看起来还可以,但是还不够好,得到的密度函数不是光滑的。观察上面的估计式子,如果记,那么估计式可以写为:
密度函数的积分:
因而只要K的积分等于1,就能保证估计出来的密度函数积分等于1。
那么一个自然的想法是,我们是不是可以换其他的函数形式呢?比如其他的分布的密度函数作为K?
比如,我可以用标准正态分布的密度函数作为K,估计就变成了:
这个密度函数的估计就变得可导了,而且积分积起来等于1。直觉上,上式就是一个加权平均,离x越近的x_i其权重越高。而最开始的估计方式则是在区间内权重相等,区间外权重为0。
当然,这里还是有h的选取问题,其原理跟上面是一样的。也因此,一般我们会把h叫做「窗宽(bandwidth)」。关于窗宽的选择方法有很多,可以plug-in,也可以用cross-validation,具体就不做赘述了。
此外还可以扩展到多维,即
其中d为x的维数,K为多维的kernel,一般为d个一维kernel的乘积。
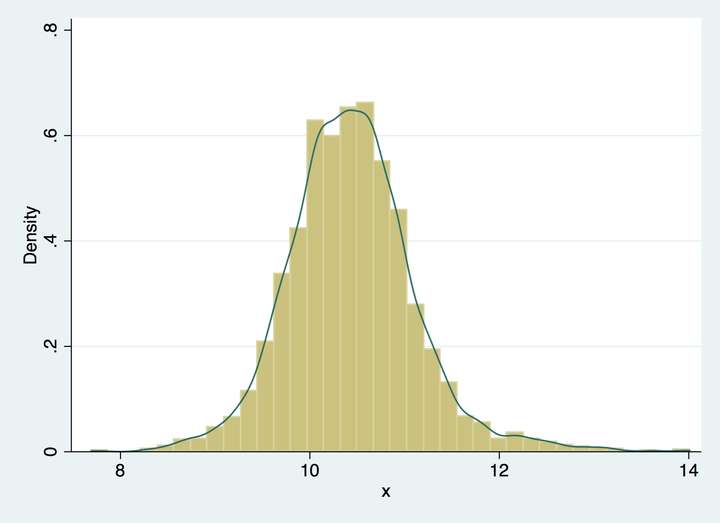
其中u与x独立,可以得到:
其中分子(这里需要用到核函数K的对称性):
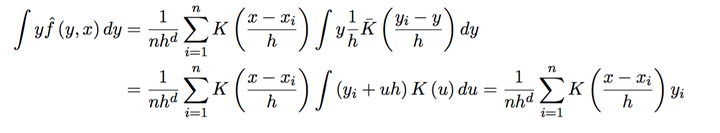
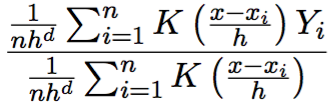
其中对于核函数K还有很多其他要求,以及高阶Kernel等等,就不一一介绍啦。感兴趣的可以参考Qi Li的书。
下面的例子输出的时空平滑口蹄疫爆发在坎布里亚,英国从第10天到231天。
colpal <- spasttopons("image.colfun")
fmdcolours <- coloura(copal(18),beks=c(-80seq(-7,length=128)))
mytimes <- 10:230
口蹄疫互动
下面是口蹄疫数据的交互式3D图。
f_breve <- spadensity(fmd_case, h = 3 , lambda = 9 , tlim = c(10, 230), sres = 32, tres = 32)
g_tilde <- bivensity(fmd_cont, h0 = 3, res = 32)原发性胆汁性肝硬化互动
下面是PBC数据的交互式三维曲面图,其中1%的公差轮廓以绿色显示。
= pbc_case, g = pbc_cont, h0 = 3.5, hp = 2, adapt = TRUE,
pilot.symmetry = "pooled", tolerate = TRUE, resol
结论
我们表明适当的阈值取决于数据的特征,并且带宽选择器算法可用于指导关于映射参数的此类决策。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python在线教育广告精准投放:SEM结构方程、XGBoost、KDE核密度、聚类、因子分析、随机森林集成优化融合用户满意度渠道效能|附代码数据
Python在线教育广告精准投放:SEM结构方程、XGBoost、KDE核密度、聚类、因子分析、随机森林集成优化融合用户满意度渠道效能|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析



