采样函数svsample需要其输入数据y是数值向量，而且没有任何缺失值（NA），如果提供其他任何内容，则会报错。
在y包含零的情况下，会发出警告，并在进行辅助混合采样之前，将大小为sd（y）/ 10000的小偏移常数添加到平方收益上。
在对数据进行处理和分析时，我们往往会遇到各种各样的情况，其中一种情况需要特别关注，那就是当变量 y 包含零值时。y 这个变量在整个数据体系中可能代表着关键的指标或者具有重要意义的数值，它的取值情况会对后续的操作产生影响。
当我们对数据进行细致的检查后发现 y 中存在零值时，这是一个需要警惕的信号。因为零值的存在可能会对后续的某些计算或者操作带来不稳定因素，甚至可能导致结果出现偏差。所以，一旦检测到 y 包含零值，系统会立即发出警告。这个警告就像是一个提醒器，告知相关的操作人员或者程序，当前的数据状态可能存在潜在的问题，需要引起重视。
警告发出之后，我们并不会直接进入下一步操作，而是需要对数据进行一定的预处理。具体来说，在进行辅助混合采样之前，我们会对平方收益进行一个调整。这里的平方收益是数据处理过程中的一个重要中间结果，它可能会受到 y 取值的影响。为了减少零值带来的潜在影响，我们会给平方收益添加一个小偏移常数。这个小偏移常数的大小是根据 y 的标准差（用 sd(y) 表示）来确定的，具体为 sd(y) 的万分之一，即 sd(y) / 10000。
添加这个小偏移常数的目的是为了让平方收益的值稍微发生改变，从而避免因为零值而导致的一些特殊情况。例如，在某些计算中，零值可能会使得分母为零，进而引发错误；或者在某些算法中，零值可能会使得结果过于极端或者不稳定。通过添加这个小偏移常数，可以在一定程度上平滑数据，让后续的辅助混合采样过程更加稳定和可靠。
总之，当 y 包含零值时，发出警告并对平方收益添加小偏移常数是一种有效的数据预处理策略，它能够帮助我们更好地应对数据中的特殊情况，提高后续分析和计算的准确性和稳定性。
但是，我们通常建议完全避免零收益数据，例如通过预先降低零收益。下面是如何使用样本数据集进行说明。
MCMC概述
从名字我们可以看出，MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。要弄懂MCMC的原理我们首先得搞清楚蒙特卡罗方法和马尔科夫链的原理。Gibbs采样是蒙特卡洛方法求解过程的一个重要的通用采样方法。
MCMC为谁而生？
蒙特卡罗原来是一个赌场的名称，用它作为名字大概是因为蒙特卡罗方法和赌术活动本质上都是一种随机模拟或者说是概率统计的方法。虽然取了这个名字，但是MCMC并不是用于赌博，最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。举个例子，假如现在要求以下积分问题：
如果我们很难求解出f(x)的原函数，那么这个积分比较难求解。这时候我们可以通过蒙特卡罗方法来模拟求解近似值。如何模拟呢？
则一个简单的近似求解方法是在[a,b]之间随机的采样一个点。比如x,然后用f(x)代表在[a,b]区间上所有的f(x)的值。那么我们可以采样[a,b]区间的n个值：用它们的均值来代表[a,b]区间上所有的f(x)的值。虽然上面的方法可以一定程度上求解出近似的解，但是它隐含了一个假定，即x在[a,b]之间是均匀分布的，而绝大部分情况，x在[a,b]之间不是均匀分布的。如果我们用上面的方法，则模拟求出的结果很可能和真实值相差甚远。
怎么解决这个问题呢？我们可以用期望的方法来求这个式子的值。而计算期望的一个近似方法是取若干个基于分布p(x)的采样点，然后求平均值得到。
上式最右边的这个形式就是蒙特卡罗方法的一般形式。当然这里是连续函数形式的蒙特卡罗方法，但是在离散时一样成立。
到现在为止，根据MCMC表达式现在的问题变成了如何基于分布P(x)采样出若干个样本？
概率分布采样
在统计模拟中，有一个很重要的问题就是给定一个概率分布P(x),如何去采样基于这个概率分布的n个x的样本集。对于常见的均匀分布uniform(0,1)是非常容易采样样本的，一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过uniform(0,1)的样本转换而得。
但是总有一些分布，尤其是很复杂的分布，我们是没法通过这种转换得到相对分布的样本集的，如积分无法显示的计算，也就无法方便的生成样本，此时我们就需要更加复杂的随机模拟的方法来生成样本，而Gibbs采样就可以解决这个难题。
准备数据
采样函数svsample期望其输入数据y是数字矢量，而没有任何缺失值（NA），如果提供其他任何内容，则会引发错误。在y包含零的情况下，发出警告，并在进行辅助混合采样之前，将大小为sd（y）/ 10000的小偏移常数添加到平方收益上。
但是，我们通常建议完全避免零收益数据，例如通过预先降低零收益。下面是如何使用样本数据集进行说明。
图1提供了该数据集中时间序列的可视化。
视频
【讲解】Python用LSTM长短期记忆网络GARCH对SPX指数金融时间序列波动率滚动预测
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
R> par(mfrow = c(2, 1), mar = c(1.9, 1.9, 1.9, 0.5), mgp = c(2, 0.6, 0))
R> plot(exrates$date, exrates$USD, type = "l",
+ main = "Price of 1 EUR in USD")
R> plot(exrates$date[-1], ret, type = "l", main = "Demeaned log returns")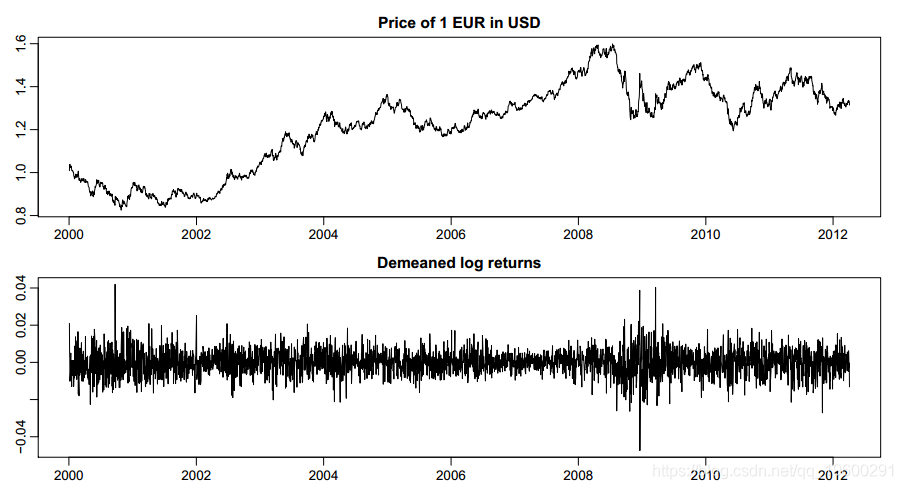
在数据处理和分析领域，数据来源十分关键。除了使用从现实世界中收集到的数据开展相关工作外，我们还能借助内置的模拟数据生成器 svsim。
svsim 是一个功能独特的模拟数据生成器，它专门针对随机波动（Stochastic Volatility，简称 SV）流程进行实现。随机波动模型在金融领域、时间序列分析等诸多方面有着广泛应用，它能够对金融资产价格波动的时变性和聚集性等特征进行有效刻画。
当我们调用 svsim 函数时，它会基于 SV 流程的特定规则和算法，生成符合该流程特征的模拟数据。该函数的返回值是一个 svsim 类的对象。这个对象可不是普通的数据集合，它具有一系列强大的功能，这些功能以方法的形式呈现。
具体来说，这个 svsim 类的对象拥有 print、summary 和 plot 这几个方法。print 方法可以让我们方便地将对象中的数据信息以一种直观的方式输出，这样我们就能快速了解数据的大致情况。summary 方法则会对数据进行更为详细的统计分析和概括，它会计算诸如均值、中位数、标准差等统计量，帮助我们深入把握数据的特征和分布情况。而 plot 方法则为我们提供了一种可视化的手段，它能够将生成的模拟数据以图形的形式展示出来，比如折线图、柱状图等。通过可视化，我们可以更清晰地观察数据的变化趋势、波动情况等，从而为后续的分析和决策提供有力支持。
除了现实世界的数据外，还可以使用内置的模拟数据生成器svsim。此函数仅对SV流程的实现，并返回svsim类的对象，该对象具有自己的print，summary和plot方法。
下面给出了使用svsim的示例代码，该模拟实例显示在图2中。
R> par(mfrow = c(2, 1))
R> plot(sim)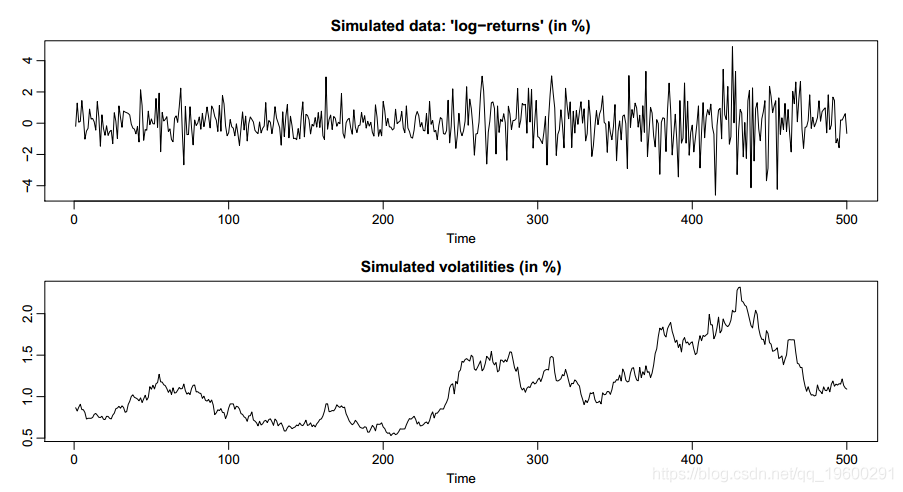
运行采样器
函数svsample，它用作C语言中实际采样器的R-wrapper 。此函数的示例用法在下面的代码中提供了默认输出。
Calling GIS_C MCMC sampler with 11000 iter. Series length is 3139.
0% [+++++++++++++++++++++++++++++++++++++++++++++++++++] 100%
Timing (elapsed): 12.92 seconds.
851 iterations per second.
Converting results to coda objects... Done!
Summarizing posterior draws... Done!可以看出，该函数调用主MCMC采样器并将其输出转换为与coda兼容的对象。后者的完成主要是出于兼容性的考虑，并且可以直接访问收敛诊断检查。
svsample的返回值是svdraws类型的对象，该对象是具有八个元素的命名列表，其中包含（1）参数在para中绘制，（2）潜在的对数波动率，（3）初始潜在的对数波动率绘制latent0，（4）y中提供的数据，（5）运行时中的采样运行时，（6）先验中的先验超参数，（7）细化的参数值，以及（8）这些图的汇总统计信息，以及一些常见的转换。
评估输出并显示结果
按照常规做法，可使用svdraws对象的print和summary方法。每个参数都有两个可选参数showpara和showlatent，用于指定应显示的输出。如果showpara为TRUE（默认设置），则会显示参数绘制的值/摘要。如果showlatent为TRUE（默认值），则显示潜在变量绘制的值/摘要。在下面的示例中，仅显示参数绘制的摘要。
Summary of 10000 MCMC draws after a burn-in of 1000.
Prior distributions:
mu ~ Normal(mean = -10, sd = 1)
(phi+1)/2 ~ Beta(a0 = 20, b0 = 1.1)
sigma^2 ~ 0.1 * Chisq(df = 1)
Posterior draws of parameters (thinning = 1):
mean sd 5% 50% 95% ESS
mu -10.1366 0.22711 -10.4749 -10.1399 -9.7933 4552
phi 0.9935 0.00282 0.9886 0.9938 0.9977 397
sigma 0.0656 0.01001 0.0509 0.0649 0.0830 143
exp(mu/2) 0.0063 0.00075 0.0053 0.0063 0.0075 4552
sigma^2 0.0044 0.00139 0.0026 0.0042 0.0069 143
（1）volplot：绘制潜在波动率的分位数，以百分比表示，即随时间变化的后验分布的经验分位数。常用的可选参数包括n步波动率的预测，x轴上标签的日期以及一些图形参数。下面的代码片段显示了一个典型示例，图3显示了其输出。
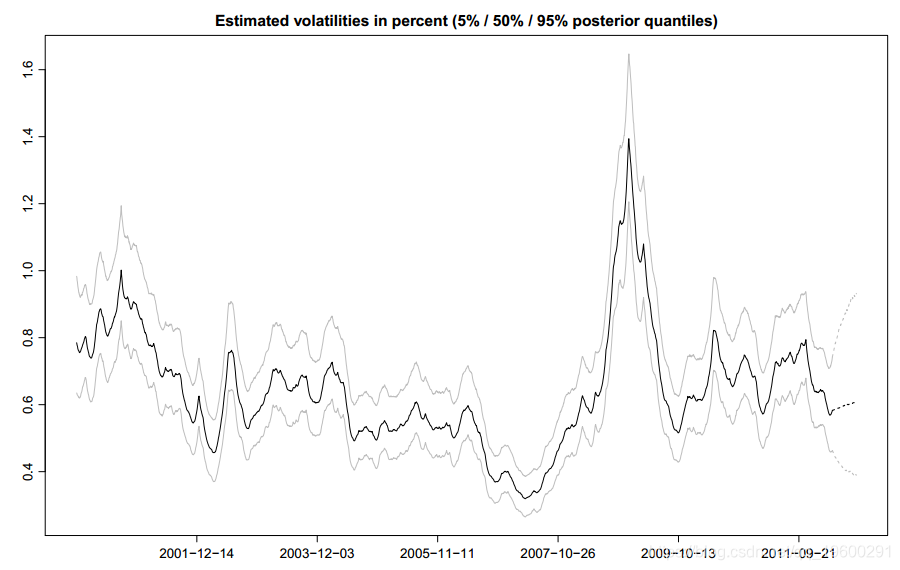
想了解更多关于模型定制、咨询辅导的信息？
（2）paratraceplot：显示θ中包含的参数的轨迹图。图5显示了一个示例。
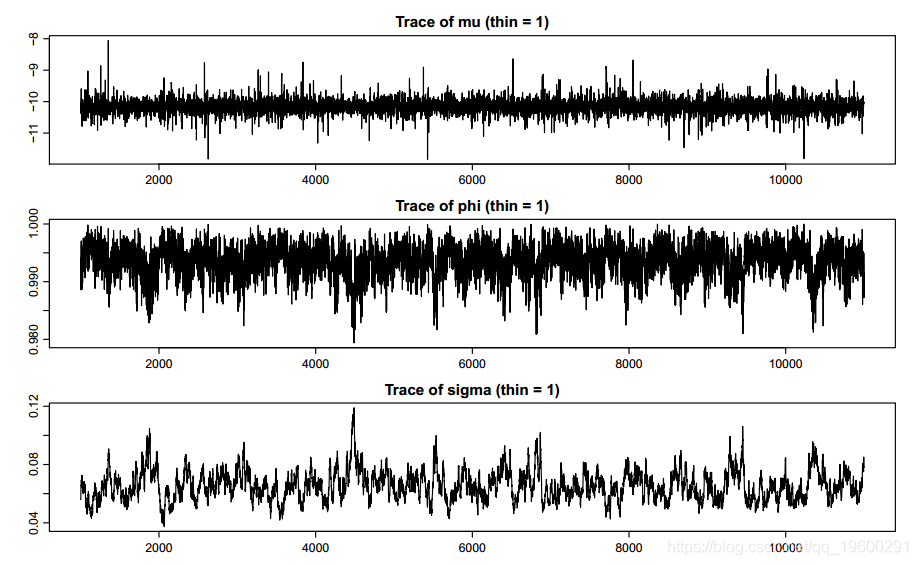
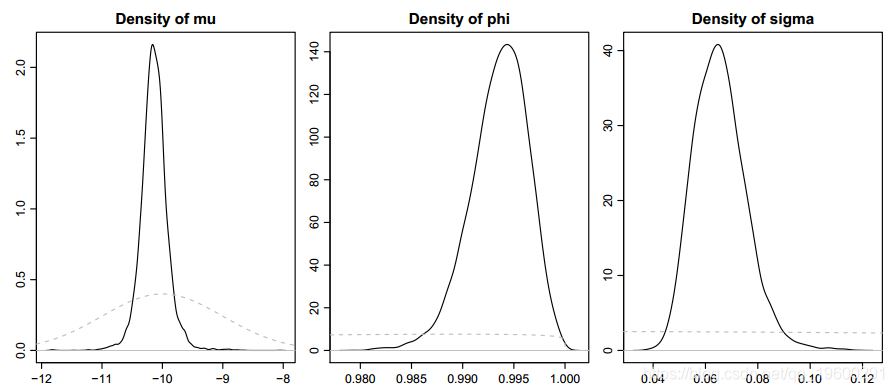
（3）paradensplot：显示θ中包含的参数的核密度估计。
为了更快地绘制较大的后验样本，应将此参数设置为FALSE。如果参数showprior为TRUE（默认值），则先验分布通过虚线灰色线指示。
图6显示了从汇率提取数据集中获得的EUR-USD汇率的示例输出。
svdraws对象的通用绘图方法将上述所有图合并。可以使用上述所有参数。请参见图7。
R> plot(res, showobs = FALSE)随时关注您喜欢的主题
为了提取标准化残差，可以在给定的svdraws对象上使用残差方法。使用可选的参数类型，可以指定摘要统计的类型。
当前，类型允许为“平均值”或“中位数”，其中前者对应于默认值。此方法返回svresid类的实向量，其中包含每个时间点所请求的标准化残差的摘要统计量。还有一种绘图方法，当参数origdata给定时，提供了将标准化残差与原始数据进行比较的选项。请参见下面的代码，对于相应的输出，请参见图8。
R> myresid <- resid(res)
R> plot(myresid, ret)
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python比特币价格时间序列：LGBMRegressor递归自回归、随机游走及外部变量预测探索
Python电影市场特征：AR模型时间序列趋势预测、热图可视化评分影响分析IMDb数据|附数据代码
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
