人工神经网络最初是由研究人员开发的,他们试图模仿人脑的神经生理学。
通过将许多简单的计算元素(神经元或单元)组合成高度互连的系统,这些研究人员希望产生诸如智能之类的复杂现象。
什么是神经网络?
神经网络是一类灵活的非线性回归,判别模型。通过检测数据中复杂的非线性关系,神经网络可以帮助做出有关实际问题的预测。
无论是线性回归模型,还是分类模型,本质上都是把数据进行映射,既可以映 射到一个或者多个离散的标签上,也可以映射到连续的空间里。单个神经元模型在 没有加入激活函数之前,可以看作一个线性回归模型,把输入的数据映射到一个 ![[公式]](https://www.zhihu.com/equation?tex=n) 维的平面空间中。
维的平面空间中。
在线性模型中,模型的输出为输入的加权和。假设一个模型的输出 和输入属性
满足关系,那么该模型就是一个线性模型。
其中, 和
为线性模型的参数。因此,线性模型具有很好的解析性,参数
表示每个属性
在回归过程中的重要程度。
线性模型的特点是任意线性模型的组合仍然是线性模型。当 时,上式为
,形成平面坐标系上的一条直线地;类似,当
时,模型中的输入
和 输出
形成在
维空间中的一个平面。细心的读者会发现该线性模型实际上就是1中神经元模型中的一部分(神经元没有加入激活函数之前)。
可遗憾的是,对于现实世界的数据来说,很多时候数据都是线性不可分的,因 此需要非线性模型。一个没有激活函数的神经元模型只是一个线性回归模型,它的 表达能力有限,不能表示复杂的数据分布。因此,我们需要在神经元中加入一个非 线性函数(称为激活函数),这就相当于为该神经元引入了非线性因素,从而使神经 元模型更好地解决复杂的数据分布问题。
神经元模型不仅可以看作对生物神经元的模拟,而且能够有效处理数学中的非 线性数据。理论上,由多个神经元组合而成的神经网络可以表示成任何复杂的函数。
神经网络对于存在以下条件的预测问题特别有用:
- 尚无将输入与输出相关的数学公式。
- 预测模型比解释模型更重要。
- 有很多训练数据。
神经网络的常见应用包括信用风险评估,营销和销售预测。
neuralNet 基于多层感知器(MLP),具有以下特征:
- 有任意数量的输入
- 在隐藏层和输出层中使用线性组合函数
- 在隐藏层中使用S型激活函数
- 具有一个或多个包含任意数量单位的隐藏层
使用神经网络函数
该 neuralNet 通过最小化的目标函数训练网络。
开发神经网络时,需要做出许多参数选择:要使用的输入数量,要使用的基本网络体系结构,要使用的隐藏层数量,每个隐藏层的单位数量,要使用的激活函数使用等等。
您可能根本不需要任何隐藏层。线性模型和广义线性模型可用于多种应用。
而且,即使要学习的函数是轻微的非线性,如果数据太少或噪声太大而无法准确估计非线性,使用简单的线性模型也可能会比使用复杂的非线性模型获得更好的效果。最简单的方法是从没有隐藏单元的网络开始,然后一次添加一个隐藏单元。然后估计每个网络的误差。当误差增加时,停止添加隐藏的单位。
如果有足够的数据,足够多的隐藏单元和足够的训练时间,则只有一个隐藏层的MLP可以学习到几乎任何函数的准确性。
生成神经网络模型的独立SAS评分代码
训练和验证神经网络模型后,可以使用该模型对新数据进行评分。可以通过多种方式对新数据进行评分。
一种方法是提交新数据,然后运行模型,通过SAS Enterprise Miner或SAS Visual Data Mining and Machine Learning使用数据挖掘来对数据进行评分,以生成评分输出。
本示例说明如何使用 neuralNet操作为ANN模型生成独立的SAS评分代码。SAS评分代码可以在没有SAS Enterprise Miner许可证的SAS环境中运行。
创建和训练神经网络
annTrain 将创建并训练一个人工神经网络(ANN),用于分类,回归的函数。
本示例使用Iris 数据集创建多层感知器(MLP)神经网络。Fisher(1936)发表的Iris数据包含150个观测值。萼片长度,萼片宽度,花瓣长度和花瓣宽度以毫米为单位测量从各三个物种50个标本。四种测量类型成为输入变量。种类名称成为名义目标变量。目的是通过测量其花瓣和萼片尺寸来预测鸢尾花的种类。
随时关注您喜欢的主题
您可以通过以下DATA步骤来将数据集加载到会话中。
data mycas.iris;
set sashelp.iris;
run;Iris数据中没有缺失值。这是很重要的,因为annTrain 操作将从模型训练中剔除包含缺失数据的观察值。如果要用于神经网络分析的输入数据包含大量缺失值的观测值,则应在执行模型训练之前替换或估算缺失值。因为Iris数据不包含任何缺失值,所以该示例不执行变量替换。
该示例使用 annTrain 来创建和训练神经网络。神经网络根据其萼片和花瓣的长度和宽度(以毫米为单位)的输入来预测预测鸢尾花种类的函数。
target="species"
inputs={"sepallength","sepalwidth","petallength","petalwidth"}
nominals={"species"}
hiddens={2}
maxiter=1000
seed=12345
randDist="UNIFORM"
scaleInit=1
combs={"LINEAR"}
targetAct="SOFTMAX"
errorFunc="ENTROPY"
std="MIDRANGE"
validTable=vldTable - 使用
sampling.Stratified操作Iris按目标变量对输入数据进行分区Species。 - 将分区指示列添加
_Partind_到输出表。该_Partind_列包含映射到数据分区的整数值。 - 创建一个由30%的表观察值组成的采样分区
Species。剩余的70%的表观测值构成第二个分区。 - 指定
12345要用于采样函数的随机种子值 。 - 命名
sampling_stratified操作创建的输出表 (带有新的分区信息列)iris_partitioned。如果内存中存在具有该名称的表,则现有表将被新iris_partitioned表内容覆盖 。 - 在源表中指定所有变量,将其传输到采样的表中。
- 使用新添加的分区列中的数据创建单独的表,以进行神经网络训练和验证。令训练表
trnTable为表 中所有观察iris_partitioned值的子集, 其中列的整数值_Partind_等于1。 - 使用新添加的分区列中的数据创建单独的表,进行神经网络训练和验证。假设验证表
vldTable是表 中所有观察iris_partitioned值的子集, 其中列的整数值_Partind_等于0。 annTrain通过使用trnTable带有目标变量的表,来创建和训练MLP神经网络Species。- 指定四个输入变量用作ANN分析的分析变量。
- 要求将目标变量
Species视为分析的名义变量。 - 为神经网络前馈模型中的每个隐藏层指定隐藏神经元的数量。例如,
hiddens={2}用两个隐藏的神经元指定一个隐藏层。 - 指定在寻求目标函数收敛时要执行的最大迭代次数。
- 指定用于执行采样和分区任务的随机种子。
- 要求将UNIFORM分布用于随机生成初始神经网络连接权重。
- 指定连接权重的比例因子,该比例是相对于上一层中的单位数的。
scaleInit参数的默认值为 1。将参数的值设置scaleInit为2会增加连接权重的比例。 - 为每个隐藏层中的神经元指定LINEAR组合函数。
- 在输出层中为神经元指定激活函数。默认情况下,SOFTMAX函数用于名义变量。
- 指定误差函数来训练网络。ENTROPY是名义目标的默认设置。
- 指定要在区间变量上使用的标准化。当
std参数的值为MIDRANGE时,变量将标准化到0和1。 - 指定要用于验证表的输入表名称。这样可以通过使用
optmlOpt参数来尽早停止迭代过程 。 - 指定
Nnet_train_model作为输出表。 - 启用神经算法求解器优化工具。
- 指定250次最大迭代以进行优化,并指定1E–10作为目标函数的阈值停止值。
- 启用LBFGS算法。LBFGS是准牛顿方法族中的一种优化算法,它通过使用有限的计算机内存来近似Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法。
- 使用频率参数来设置验证选项。当
frequency参数的值为1时,将在每个时期进行验证。当frequency为0时,将不进行任何验证。
输出显示数据的概述。
输出:列信息
来自table.columnInfo的结果
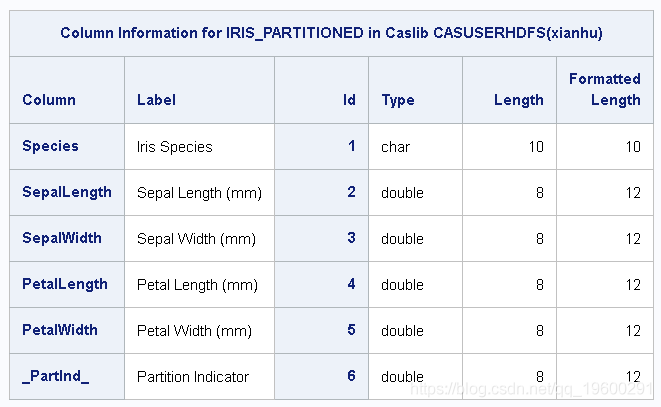
如果在输入表上使用table.fetch 命令,则可以查看输出2中显示的示例数据行 。
输出2:已提取的行
来自table.fetch的结果
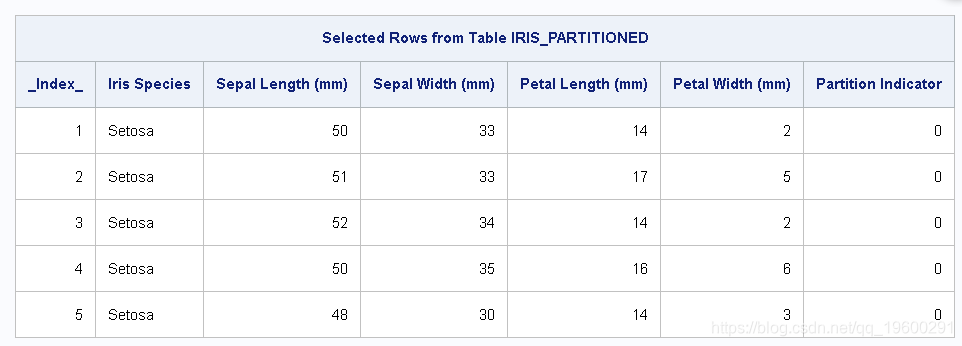
如果simple.freq 在输入表上使用命令,则可以验证三种种类中每种都有50个观测值,输入数据表中总共有150个观测值,如输出3所示。
输出 3:物种频率
来自simple.freq的结果
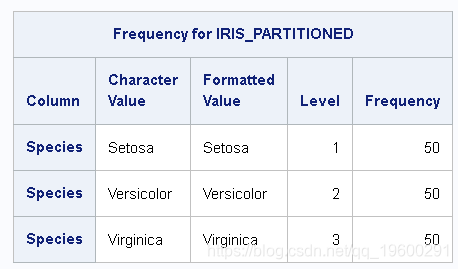
Iris 通过成功完成输入表的neuralNet.annTrain训练过程后 ,结果将显示训练数据迭代历史记录,其中包含目标函数,损失和验证误差列,如 输出4中所示。
输出 4:优化迭代历史记录
来自NeuroNet.annTrain的结果
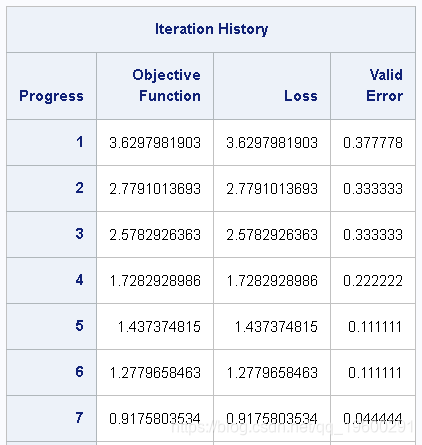
在“迭代历史记录”表下方,您应该看到“收敛状态”表。对于成功的神经网络模型,“收敛状态”应报告“优化已收敛”,如 输出 5中所示。
输出 5:收敛状态
成功的模型训练包括输出模型的摘要结果,如输出 6所示 。
输出 6:模型信息
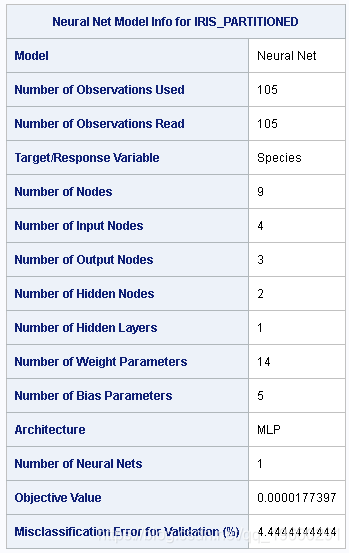
这些结果重申了关键的模型构建因素,例如模型类型;目标变量 神经网络模型输入,隐藏和输出节点的摘要;权重和偏差参数;最终目标值;以及评分验证数据集的误分类误差。
在表格底部,您将看到由验证数据确定的最终误分类错误百分比。如果将这个神经网络模型用作预测函数,并且您的数据来自与Iris 验证表具有相同数据分布,则 可以预期93%–94%的物种预测是正确的。
使用神经网络模型对输入数据进行评分
训练和验证神经网络模型后,可以使用该模型对新数据进行评分。最常见的技术是通过SAS Enterprise Miner或SAS Visual Data Mining and Machine Learning使用数据挖掘环境来生成评分输出,从而提交新数据并运行模型以对新数据评分。
拥有训练的神经网络后,可以使用该神经网络模型和 annScore 操作对新的输入数据进行评分,如下所示:
table=vldTable
modelTable="train_model"; - 识别训练数据表。训练数据是
iris_partitioned表中的观测值,在分区指示符列(_partind_)中的值为0 。 - 确认验证数据表。验证数据是
iris_partitioned表中的观察值,在分区指示符列(_partind_)中的值为1 。 - 对训练数据进行评分。提交输入数据,该 数据将由经过训练的神经网络模型评分。因为在此代码块中要评分的数据是模型训练数据,所以您应该期望评分代码读取所有105个观察值,并以0%错误分类错误预测目标变量值。模型训练数据包含已知的目标值,因此,在对模型训练数据进行评分时,应期望其分类错误为0%。
- 对验证数据评分。该操作将提交输入数据,在SAS数据挖掘环境中,由经过训练的神经网络模型对输入数据进行评分。验证数据包含已知目标值,但训练算法不会读取验证数据。算法预测验证数据中每个观察值的目标值,然后将预测值与已知值进行比较。分类误差百分比是通过从1中减去正确预测的分类百分比来计算的。较低的分类误差百分比通常表示模型性能更好。
验证数据包含30%的原始输入数据观察值,并按目标变量Species分层 。原始数据包含每个种类的50个观察值;验证数据(30%)包含三种物种中每一种的比例15个观测值,总共45个观测值。如果验证数据中的45个观察值中有42个被正确分类,则该模型的错误分类误差为6.67%。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测
SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测 Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据
Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据 Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据
Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据 MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据
MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据



