R语言rjags使用随机效应进行臭氧数据分析

由Kaizong Ye，Coin Ge撰写

加载和格式化数据

可下载资源

rm(list=ls())
 ls()
## [1] "s" "Y"
dim(Y)
## [1] 1106   31
dim(s)
## [1] 1106    2
ns   <- nrow(Y)
  
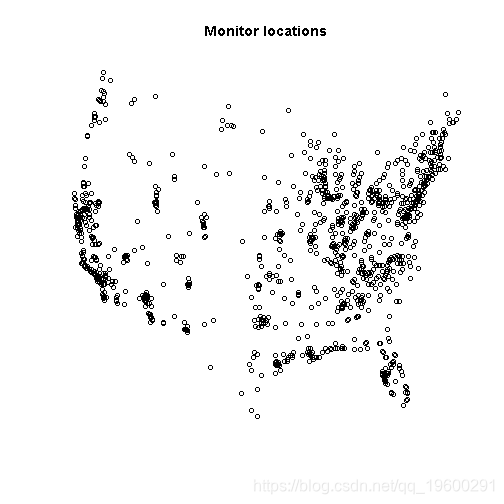
plot(s,axes=FALSE,xlab="",ylab="",main="Monitor locations")

普通的线性回归只包含两项影响因素，即固定效应（fixed-effect）和噪声（noise）。噪声是我们模型中没有考虑的随机因素。而固定效应是那些可预测因素，而且能完整的划分总体。例如模型中的性别变量，我们清楚只有两种性别，而且理解这种变量的变化对结果的影响。

那么为什么需要 Mixed-effect Model？因为有些现实的复杂数据是普通线性回归是处理不了的。例如我们对一些人群进行重复测量，此时存在两种随机因素会影响模型，一种是对某个人重复测试而形成的随机噪声，另一种是因为人和人不同而形成的随机效应（random effect）。如果将一个人的测量数据看作一个组，随机因素就包括了组内随机因素（noise）和组间随机因素（random effect）。这种嵌套的随机因素结构违反了普通线性回归的假设条件。

你可能会把人员（组间的随机效应）看作是一种分类变量放到普通线性回归模型中，但这样作是得不偿失的。有可能这个factor的level很多，可能会用去很多自由度。更重要的是，这样作没什么意义。因为人员ID和性别不一样，我们不清楚它的意义，而且它也不能完整的划分总体。也就是说样本数据中的路人甲，路人乙不能完全代表总体的人员ID。因为它是随机的，我们并不关心它的作用，只是因为它会影响到模型，所以不得不考虑它。因此对于随机效应我们只估计其方差，不估计其回归系数。

混合模型中包括了固定效应和随机效应，而随机效应有两种方式来影响模型，一种是对截距影响，一种是对某个固定效应的斜率影响。前者称为 Random intercept model，后者称为 Random Intercept and Slope Model。Random intercept model的函数结构如下

Yij = a0 + a1*Xij + bi + eij

a0: 固定截距
a1: 固定斜率
b: 随机效应（只影响截距）
X: 固定效应
e: 噪声

混合线性模型有时又称为多水平线性模型或层次结构线性模型由两个部分来决定，固定效应部分+随机效应部分.

绘制臭氧探测器位置数据

 abline(75,0,col=2)

用箱线图来表示臭氧水平随着时间变化

 abline(75,0,col=2)

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

在JAGS中指定模型

Ozone_model <- "model{

   # Likelihood
 

   # Random effects
   for(i in 1:ns){
    alpha i] ~ dnorm(0, )
   }
   for(j in 1:nt){
    gamma j] ~ dnorm(0, )
   }

   # Priors
   mu   ~ dnorm(0,0.01)
 

   # Output the parameters of interest
   sigma2[1] <- 1/taue
 ] 
   pct[1]    <- sigma2[1]/sum(sigma2[])   
   pct[2]    <- sigma2[2]/sum(sigma2[])   
   pct[3]    <- sigma2[3]/sum(sigma2[])   

  }"

模型

dat    <- list(Y=Y,ns=ns,nt=nt)
model1 <- jags.model(textConnection(Ozone_model),inits=init,data = dat, n.chains=1)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
##    Graph Size: 69733
## 
## Initializing model

最受欢迎的见解

1.matlab使用贝叶斯优化的深度学习

2.matlab贝叶斯隐马尔可夫hmm模型实现

3.R语言Gibbs抽样的贝叶斯简单线性回归仿真

4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

5.R语言中的Stan概率编程MCMC采样的贝叶斯模型

6.Python用PyMC3实现贝叶斯线性回归模型

7.R语言使用贝叶斯层次模型进行空间数据分析

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.matlab贝叶斯隐马尔可夫hmm模型实现

   summary(samp)

## 
## Iterations = 10001:30000
## Thinning interval = 1 
## Number of chains = 1 
## Sample size per chain = 20000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                Mean       SD  Naive SE Time-series SE
## gamma[1]   0.792641 0.646869 4.574e-03      3.521e-02
## gamma[2]  -0.005295 0.640672 4.530e-03      3.552e-02
## gamma[3]   1.637455 0.644532 4.558e-03      3.664e-02
## gamma[4]  -0.193925 0.648253 4.584e-03      3.685e-02
## gamma[5]  -3.486456 0.647315 4.577e-03      3.761e-02
## gamma[6]  -3.208898 0.652157 4.611e-03      3.784e-02
## gamma[7]  -4.598029 0.646555 4.572e-03      3.636e-02
## gamma[8]  -1.152366 0.646559 4.572e-03      3.740e-02
## gamma[9]   2.394293 0.646956 4.575e-03      3.715e-02
## gamma[10]  0.487923 0.644625 4.558e-03      3.733e-02
## gamma[11]  0.460761 0.644827 4.560e-03      3.636e-02
## gamma[12]  0.833041 0.651137 4.604e-03      3.649e-02
## gamma[13] -1.580735 0.651594 4.607e-03      3.672e-02
## gamma[14] -1.585905 0.647296 4.577e-03      3.760e-02
## gamma[15] -1.587356 0.647281 4.577e-03      3.744e-02
## gamma[16] -2.748602 0.644203 4.555e-03      3.740e-02
## gamma[17] -5.031267 0.647277 4.577e-03      3.710e-02
## gamma[18] -4.176877 0.648933 4.589e-03      3.655e-02
## gamma[19] -1.315643 0.648456 4.585e-03      3.730e-02
## gamma[20]  1.023326 0.648118 4.583e-03      3.502e-02
## gamma[21]  2.319419 0.652453 4.614e-03      3.625e-02
## gamma[22]  4.252081 0.642283 4.542e-03      3.672e-02
## gamma[23]  1.674201 0.648382 4.585e-03      3.726e-02
## gamma[24]  3.226205 0.649139 4.590e-03      3.647e-02
## gamma[25]  3.795414 0.650599 4.600e-03      3.717e-02
## gamma[26]  5.847544 0.653161 4.619e-03      3.616e-02
## gamma[27]  0.240722 0.651784 4.609e-03      3.609e-02
## gamma[28] -0.792185 0.649085 4.590e-03      3.542e-02
## gamma[29]  1.314577 0.648981 4.589e-03      3.578e-02
## gamma[30]  2.312463 0.643270 4.549e-03      3.774e-02
## gamma[31]  1.366669 0.645759 4.566e-03      3.719e-02
## pct[1]     0.560401 0.011415 8.072e-05      8.779e-05
## pct[2]     0.413958 0.011479 8.117e-05      9.040e-05
## pct[3]     0.025641 0.007074 5.002e-05      9.037e-05
## sigma[1]  12.948830 0.051492 3.641e-04      3.837e-04
## sigma[2]  11.130828 0.250331 1.770e-03      1.933e-03
## sigma[3]   2.746672 0.378729 2.678e-03      4.721e-03
## 
## 2. Quantiles for each variable:
## 
##               2.5%      25%       50%      75%    97.5%
## gamma[1]  -0.49380  0.36017  0.791847  1.22949  2.05602
## gamma[2]  -1.29551 -0.42523  0.001094  0.42257  1.22885
## gamma[3]   0.37334  1.20738  1.636656  2.06665  2.89512
## gamma[4]  -1.48133 -0.61898 -0.193318  0.23839  1.07346
## gamma[5]  -4.77636 -3.91313 -3.479185 -3.05709 -2.23466
## gamma[6]  -4.48775 -3.64108 -3.207367 -2.77563 -1.93379
## gamma[7]  -5.87435 -5.02716 -4.594350 -4.16119 -3.34211
## gamma[8]  -2.43738 -1.57860 -1.149767 -0.71914  0.10173
## gamma[9]   1.10795  1.97121  2.394399  2.82109  3.66081
## gamma[10] -0.78684  0.05873  0.484838  0.91732  1.75985
## gamma[11] -0.81422  0.02778  0.465699  0.89415  1.72498
## gamma[12] -0.45600  0.40278  0.841823  1.27229  2.09552
## gamma[13] -2.90014 -2.00870 -1.575470 -1.14767 -0.32264
## gamma[14] -2.87864 -2.01064 -1.581978 -1.14763 -0.35096
## gamma[15] -2.86282 -2.01560 -1.583218 -1.15679 -0.32290
## gamma[16] -4.02545 -3.17798 -2.743399 -2.31751 -1.49586
## gamma[17] -6.31465 -5.46146 -5.026931 -4.59211 -3.79179
## gamma[18] -5.46025 -4.60004 -4.176324 -3.74965 -2.91543
## gamma[19] -2.60870 -1.74448 -1.305350 -0.88302 -0.06778
## gamma[20] -0.26230  0.59741  1.024962  1.45275  2.28854
## gamma[21]  1.03505  1.88831  2.319906  2.75294  3.60079
## gamma[22]  2.98850  3.82871  4.256085  4.67533  5.52185
## gamma[23]  0.38791  1.24198  1.677333  2.10926  2.93725
## gamma[24]  1.95181  2.79313  3.226292  3.65460  4.51323
## gamma[25]  2.53324  3.36055  3.793573  4.23512  5.06812
## gamma[26]  4.57296  5.41174  5.848862  6.27689  7.15103
## gamma[27] -1.03397 -0.18368  0.235404  0.67501  1.51956
## gamma[28] -2.06357 -1.22295 -0.794349 -0.35386  0.46984
## gamma[29]  0.02345  0.88405  1.316177  1.74737  2.57636
## gamma[30]  1.04671  1.88275  2.317915  2.74095  3.57092

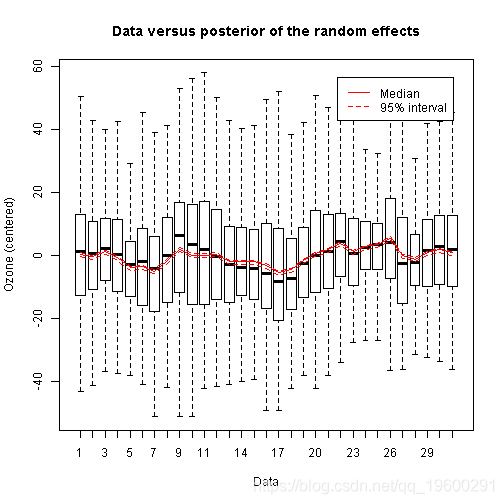
由此看来，空间位置和误差似乎是变异的最大来源，而且每日随机效应只起很小的作用。

绘制随机效果

 sum <- summary(samp)
   names(sum)
## [1] "statistics" "quantiles"  "start"      "end"        "thin"      
## [6] "nchain"
   q <- sum$quantiles

   R  <- Y-mean(Y,na.rm=TRUE)
   boxplot(R,xlab="Data",ylab="Ozone (centered)",outline=FALSE,
           main="Data versus posterior of the random effects")
   

   legend("topright",c("Median","95% interval"),lty=1:2,col=2,bg=gray(1),inset=0.05)