R语言markov switching model马尔可夫转换模型研究案例

然而，大约在1990年以后的经济扩张存在持续时间依赖性，并且对于大约1990年后的时期，持续时间依赖于收缩。此外，由持续时间依赖的马尔可夫转换模型确定的衰退日期与官方定义的衰退年表相同。

商业周期的转折点长期以来一直是公众，无论是学术界还是政府的利益点。

我们想要特别了解从收缩状态转变为扩张状态的概率在多大程度上取决于经济处于衰退状态的时间长短？同样，经济可能陷入收缩状态的可能性取决于扩张国家的长度吗？在台湾商业周期的1990年之前和1990年之后，经济衰退和扩张国家的持续时间依赖性是否保持不变？

估算程序为了找到持续时间相关马尔可夫切换模型的参数估计，可以采用准最大似然法和吉布斯采样器方法来实现估计工作。因此，我们在本文中采用后一种方法。

使用贝叶斯MCMC方法查找未知参数估计值。 对Markov切换模型的规范和估算进行了全面审查。

实验结果

用于分析商业周期波动的第一个候选系列是国民生产总值（GNP）或国内生产总值（GDP）。我们使用GDP进行实证研究，是从台湾地区的AREMOS数据库中获取的季度数据。样本从1961年到2001年开始，相当于162次观察。

我们将整个GDP的样本周期划分为两个子样本，但很难做出截止点的选择。我们论文的目的不是找到一个“真正的”结构断点。相反，我们想知道台湾1990年以后和1990年后商业周期的持续时间依赖特征。我们采用递归估计方法来检查经验结果的稳健性并概述估计步骤如下。

我们的策略是，首先在1990年之前的时期，我们通过DDMS模型从1962年到1987年估算GDP的年增长率，然后我们再添加一个观察并重新估计经验序列。从1987年到1990年重复递归估计程序。对于1990年后的时期，我们再次估计1988年至2001年的经验系列，然后我们删除了一个观察，并重复估计1988年至2001年。

Gibbs采样运行11,000次迭代，前1000次绘制被丢弃，然后保存10,000次绘制并用于计算后验分布的时刻。据发现，β的后估计1是正用于预1990和1990年以后的周期。持续时间依赖参数β2，其表示从膨胀状态将要收缩的状态，是针对1990年以前周期相对稳定。

图1收缩d个季度后从收缩状态转变为膨胀状态的概率

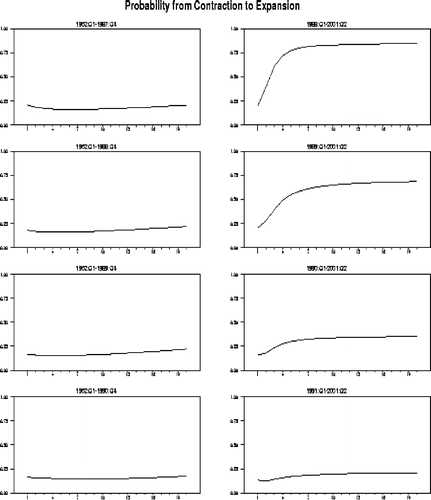
图2经过d个季度扩张后从膨胀状态转变为收缩状态的概率

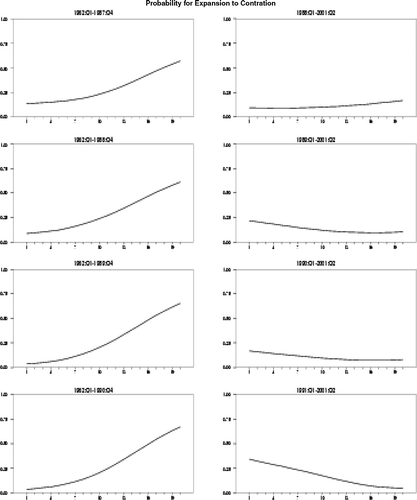
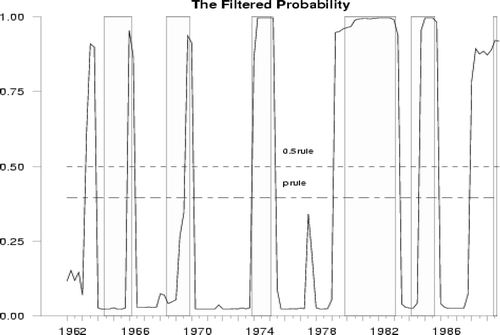
图3至图6总结了由DDMS模型确定的衰退日期的过滤概率。阴影区域是CEPD定义的衰退年代表。

马尔可夫转换模型最具创新性的方面是能够通过所谓的过滤和平滑概率客观地确定经济状态

建议使用两个标准来评估预测失败。第一个是错过的信号故障，即当经济衰退时，但模型无法预测。另一个是错误信号失败，即模型预测存在衰退，但它从未发生过。

图3由DDMS模型（1962-1988）确定的衰退日期的过滤概率。阴影区域是CEPD定义的衰退日期

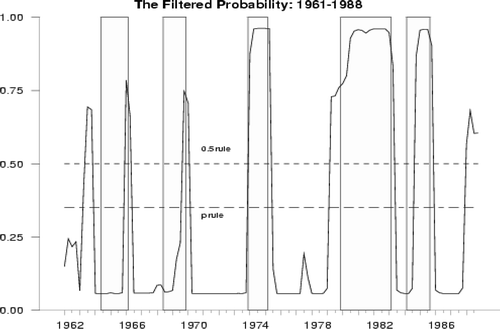
图4由DDMS模型（1989-2001）确定的衰退日期的过滤概率。阴影区域是CEPD定义的衰退日期

图5由DDMS模型（1962-1989）确定的衰退日期的过滤概率。阴影区域是CEPD定义的衰退日期

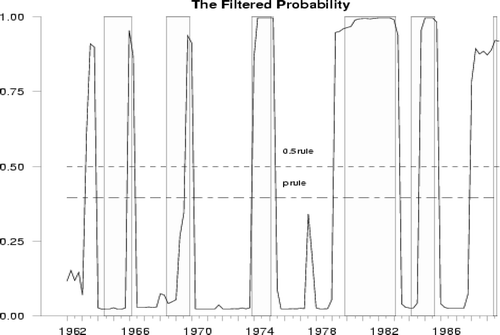
图6由DDMS模型（1990-2001）确定的衰退日期的过滤概率。阴影区域是CEPD定义的衰退日期

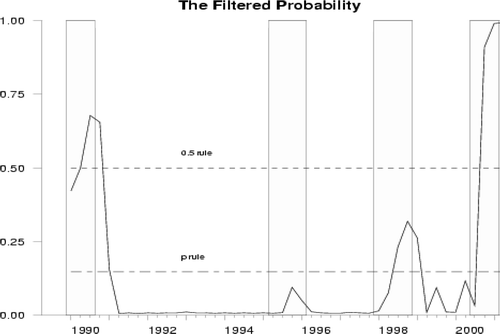
图3至图6显示了类似的模式，并产生了与1962年至1988年和1962年至1989年官方确定的衰退年表一致的衰退日期。在1989年至2001年期间，只有一个错过的信号发生在1995年左右。然而，根据0.5规则，1995年和1998年发生了1990年至2001年的两次遗漏信号。

9如果0.5规则后的预测概率超过0.5，则预计会出现衰退。

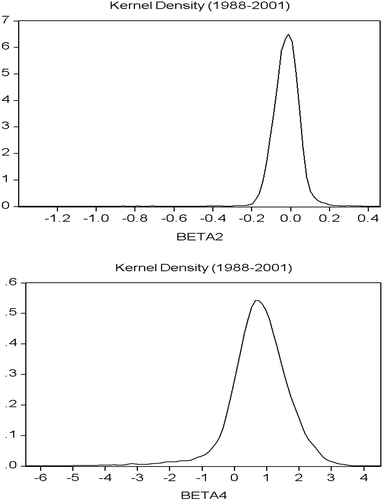
然而，令我们惊讶的是，高炉的结果并不支持大约在1990年之前的经济衰退和大约1990年后的时期的经济衰退的持续时间依赖性。

图7 β的内核密度图2和β 4（1962至1987年）

图8 β的内核密度图2和β 4（1988至2001年）

结束语

本文研究了台湾商业周期的持续时间依赖特征。首先，规范捕获持续时间依赖性是概率函数而不是逻辑函数形式。采用贝叶斯框架结合马尔可夫链蒙特卡罗方法而不是QMLE来实现估计工作。