
正如有配偶的寿命之间存在很强的相关性,我们可能会问,孩子和孙子的出生是否具有对一个人的剩余生命的影响(或者我们是否可以像这样假设独立性)。
最近我们被客户要求撰写关于死亡率建模的研究报告,包括一些图形和统计输出。
死亡率建模是一种通过分析相关数据来构建模型以预测或评估特定人群或对象的死亡概率的方法。
在这个过程中,可能会收集各种因素的数据,如年龄、性别、健康状况、生活方式等,运用统计学方法和数学模型来确定这些因素与死亡率之间的关系,并据此进行预测和分析。
例如,在保险行业中,死亡率建模可以帮助确定保险费率;在公共卫生领域,可用于评估疾病对人群死亡率的影响以及制定相应的干预措施。
Lee-Carter 模型是一种用于对年死亡率进行建模预测期望寿命的模型。它通常被应用于人口统计学和精算学领域,通过分析历史死亡率数据来预测未来的死亡率趋势,进而可以推算出期望寿命等指标。该模型在人口预测、保险精算等方面有着广泛的应用。
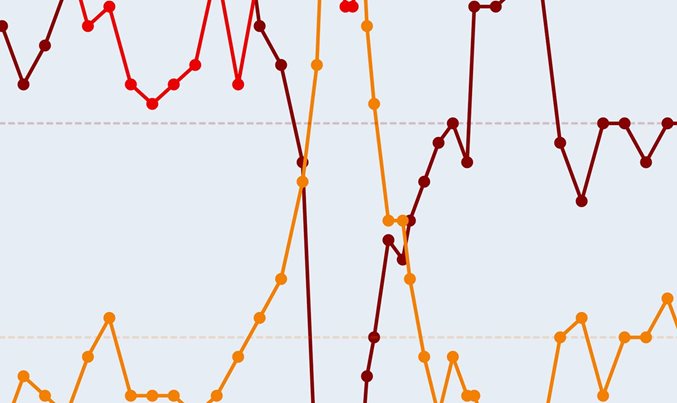
昨天上午,我们获得了分娩产妇的平均年龄两个图表,根据孩子的出生顺序排序,区间是1905-1965年:
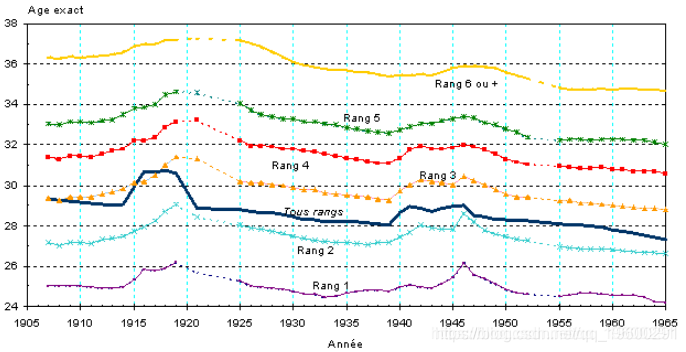
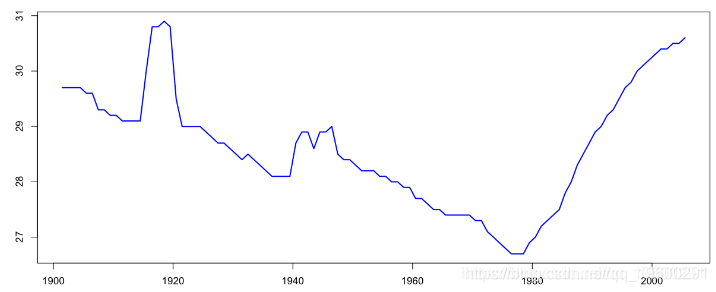
然后是1960-2000年:
Lee-Carter模型的主要思路是将死亡率的变化分解为时间因子t和年龄因子x。如果用 表示x岁的人群在第t年的中心死亡率,那么
表示x岁的人群在第t年的中心死亡率,那么 满足以下函数关系式。
满足以下函数关系式。
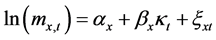 (1)
(1)
其中, 反应x岁年龄组别的对数中心死亡率的平均水平,
反应x岁年龄组别的对数中心死亡率的平均水平, 为人口死亡率随时间变化的速度,
为人口死亡率随时间变化的速度, 为年龄因子对
为年龄因子对 的敏感度,即x岁年龄组别的死亡率随着时间变化的大小,
的敏感度,即x岁年龄组别的死亡率随着时间变化的大小, 为随机误差项,假设其服从正态分布
为随机误差项,假设其服从正态分布 。为了得到唯一确定的参数估计值,加入约束条件
。为了得到唯一确定的参数估计值,加入约束条件 以及
以及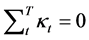 。
。 是为了保证参数
是为了保证参数 的平均值的含义,即
的平均值的含义,即 。
。
3.1. 模型的求解
Lee-Carter模型参数的估计方法主要包括矩阵奇异值分解法(SVD)、最小二乘(OLS)和加权最小二乘法(WLS);奇异值分解法和最小二乘法对不同年龄人群的死亡率赋予了相同的权重,但Koissi [2] 证明了,在现实情况下,不同年龄人群对应的人口数和死亡人口数都存在较大的差异,因此这两种方法在死亡率很低的条件下使用效果较差。为此,采用加权最小二乘法来估计Lee-Carter模型。
加权最小二乘法通过以下两个步骤求得 ,
,
第一步,将式(1)两边对年龄x 求和,得到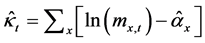 。
。
第二步,Wilmoth [3] 证明 的方差近似等于死亡人数
的方差近似等于死亡人数 的倒数,因此可以将
的倒数,因此可以将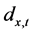 作为残差平方和的权重。最小化经加权处理后的残差平方和
作为残差平方和的权重。最小化经加权处理后的残差平方和 ,即
,即 得到
得到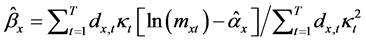 [4] 。
[4] 。
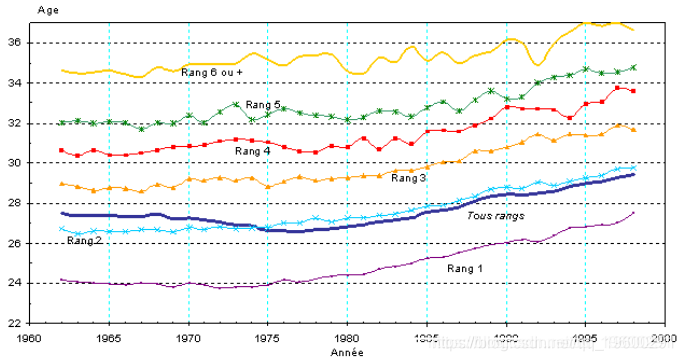
这些图形令人兴奋,特别是在过去30年中观察到的增长方面,这使我想到了寿命的增长趋势。
我们可以找到其他有趣的数据(在这种情况下为平均 出生年龄 )。
> age$Age=as.character(age$AGE)
> age$AGE=as.numeric(substr(age$Age,1,2))+
+ as.numeric(substr(age$Age,4,4))/10
> plot(age$ANNEE+.5,age$AGE,
+ type="l",lwd=2,col="blue")我们在上面的图中发现深蓝色的曲线,
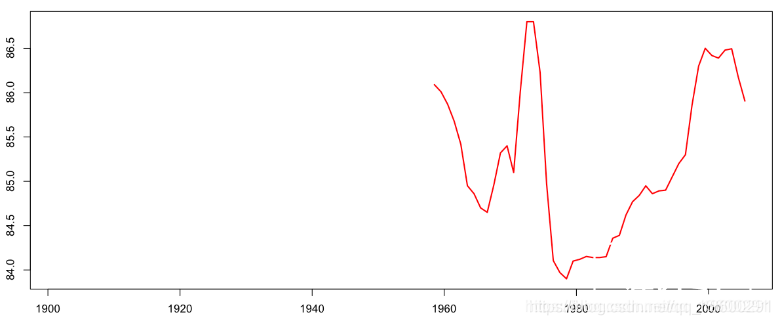
获取祖母的平均年龄,我们进一步分析
> tail(age)
AGE Age NAIS.MERE NAIS.GRD.MERE age.GRD.MERE
2000 2000 30.3 30,3 1970.2 1942.87 57.63
2001 2001 30.4 30,4 1971.1 1943.80 57.70
2002 2002 30.4 30,4 1972.1 1944.92 57.58
2003 2003 30.5 30,5 1973.0 1945.95 57.55
2004 2004 30.5 30,5 1974.0 1947.05 57.45
2005 2005 30.6 30,6 1974.9 1948.04 57.46
> plot(age$ANNEE+.5,age$age.GRD.MERE,
+ type="l",lwd=2,col="red")
想了解更多关于模型定制、咨询辅导的信息?
再一次,我们可以形象地看到外婆的出生年龄
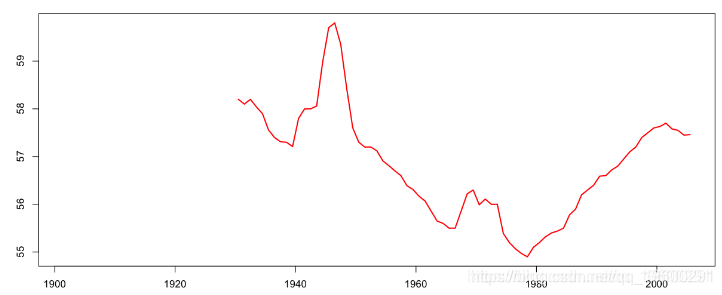
我们可以通过使用Lee-Carter模型对年死亡率进行建模,并推断到当前世纪,我们可以推断出剩余期望寿命。
> Deces <- read.table("Dec.txt",header=TRUE)
> Expo <- read.table("Expo.txt",header=TRUE,skip=2)
> Deces$Age <- as.nu
> Expo$Age <- as.numeric(as.character(Expo$Age))
> Expo$Age[is.n
Deces$Female/Expo$Female,nL,nC)
> POPF <- matrix(Expo$Female,nL,nC)
> BASEF <- demogdata(data=MUF, pop=POPF,ages=AGE,
+ years=YEAR, t
> K1 <- LCF$kt
nction(xentier,T){
+ return(ext) }
> EVIE = function(x,T){
+ x1 <- trunc(x)
> tail(age)
AGE Age NAIS.MERE NAIS.GRD.MERE age.GRD.MERE EV
2000 30.3 30,3 1970.2 1942.87 57.63 29.13876
2001 30.4 30,4 1971.1 1943.80 57.70 29.17047
2002 30.4 30,4 1972.1 1944.92 57.58 29.39027
2003 30.5 30,5 1973.0 1945.95 57.55 29.52041
2004 30.5 30,5 1974.0 1947.05 57.45 29.72511
2005 30.6 30,6 1974.9 1948.04 57.46 29.80398换句话说,在最后一行,2005年,一名57.46岁女性的(剩余)期望寿命约为29.80岁。然后,我们不仅可以看到他祖母的平均年龄,还可以看到她的剩余期望寿命,
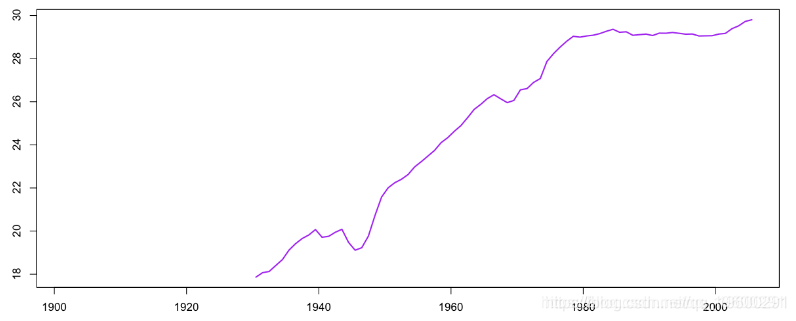
然后我们就可以确定曾祖母的(平均)年龄,
以及曾祖母的(剩余)寿命
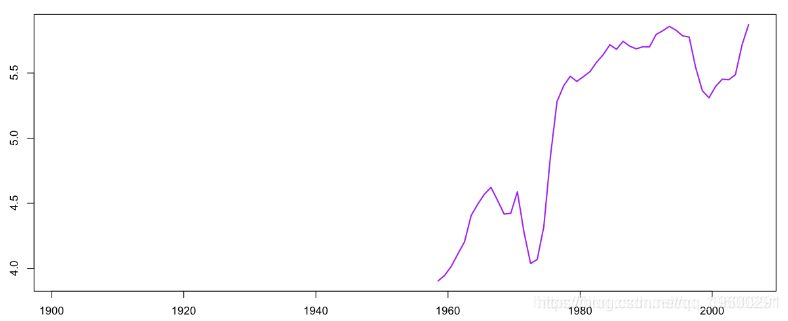
现在我们也可以对这项快速研究的局限性感到疑惑。特别是,正如有配偶的寿命之间存在很强的相关性,我们可能会问,孩子和孙子的出生是否具有对一个人的剩余生命的影响(或者我们是否可以像这样假设独立性)。

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!




 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测



