《世界幸福报告》是可持续发展解决方案网络的年度报告,该报告使用盖洛普世界民意调查的调查结果研究了150多个国家/地区的生活质量。
报告的重点是幸福的社交环境。在本项目中,我将使用世界幸福报告中的数据来探索亚洲22个国家或地区,并通过查看每个国家的阶梯得分,社会支持,健康的预期寿命,自由选择生活,慷慨,对腐败的看法以及人均GDP,来探索亚洲22个国家的相似和不同之处。
视频
KMEANS均值聚类和层次聚类:R语言分析生活幸福质量系数可视化实例
简介
我将使用两种聚类方法,即k均值和层次聚类,以及轮廓分析来验证每种聚类方法。
k-means算法简介:
K-means算法是IEEE 2006年ICDM评选出的数据挖掘的十大算法中排名第二的算法,排名仅次于C4.5算法。K-means算法的思想很简单,简单来讲就是对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大,两个对象之间的距离越近,相似性越高。聚类的结果就是使类内部的同质性高,而类之间的异质性高。
k-means算法的具体工作流程如下:
step1:导入一组具有n个对象的数据集,给出聚类个数k;
step2:从n个对象中随机取出k个作为初始聚类中心;
step3:根据欧几里得距离来判断相似度量,确定每个对象数据哪个簇;
step4:计算并更新每个簇中对象的平均值,并将其定为每个簇的新的聚类中心;
step5:计算出准则函数E;
step6:循环step3,step4,step5直到准则函数E在允许的误差范围内;
k-means算法的几个主要特点:
发现球形互斥的簇:由于K-means算法一般是以欧几里得距离作为相似性度量指标,所以K-means算法对于球形互斥的簇的聚类效果会比较好;
对低维数据集效果较好:同样的数据量,维度越高,数据矩阵越稀疏,当数据维度比较高时,数据矩阵是一个稀疏矩阵,K-means算法稀疏矩阵数据聚类效果不佳;
容易陷入局部最优:对于K-means算法来说,初始聚类中心的确定十分重要,因为不同的聚类中心会使算法沿着不同的路径搜索最优聚类结果,不过对于陷入局部最优这个问题可以从初始聚类中心的选择来进行改进。
将要分析的国家和地区是:
asia <- w filer(gepl('Asia', Rgion)

探索性数据分析
相关矩阵
pair(aia\[,-c(1,2)\], sal=TUE,col,hst.ol)
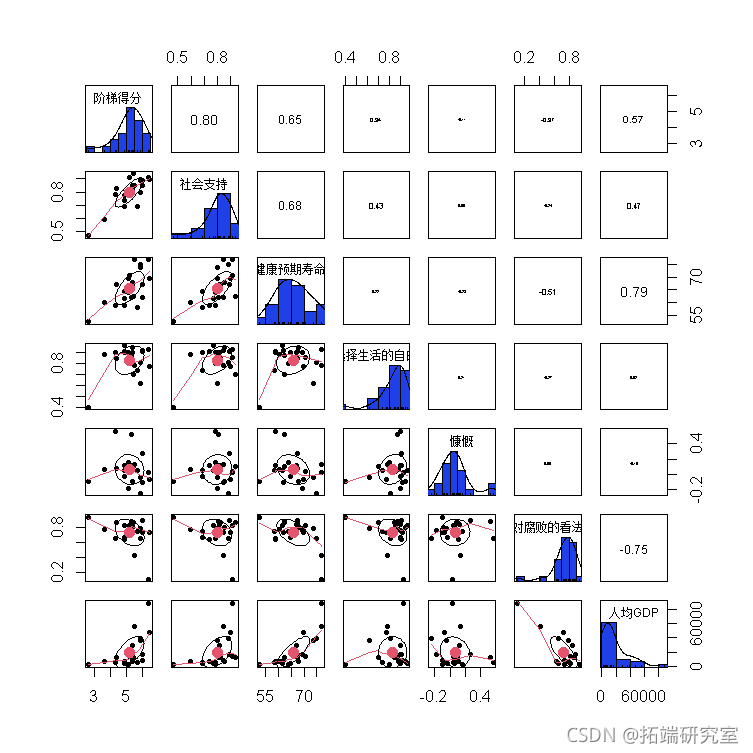
- 阶梯得分,社会支持,生活选择的自由以及对腐败的看法的分布是左偏的。
- 慷慨和人均GDP的分布是右偏的。
- 健康预期寿命的偏差大约是对称的。
- 两者之间存在很强的正相关关系:
- 阶梯分数和社会支持
- 健康预期寿命和人均GDP
- 之间存在强烈的负相关关系:
- 对腐败的看法和人均GDP
- 之间存在中等正相关:
- 阶梯得分和健康预期寿命
- 社会支持与健康预期寿命
- 人均GDP较高的国家往往对腐败的看法较低,对健康的预期寿命,社会支持和阶梯得分较高。
国家和地区比较
grd.rrnge( ggplt(sia, es(rerder(x=fctor(国家名称), 阶梯得分, FN=min), y=阶梯得分, fill=区域指标)))
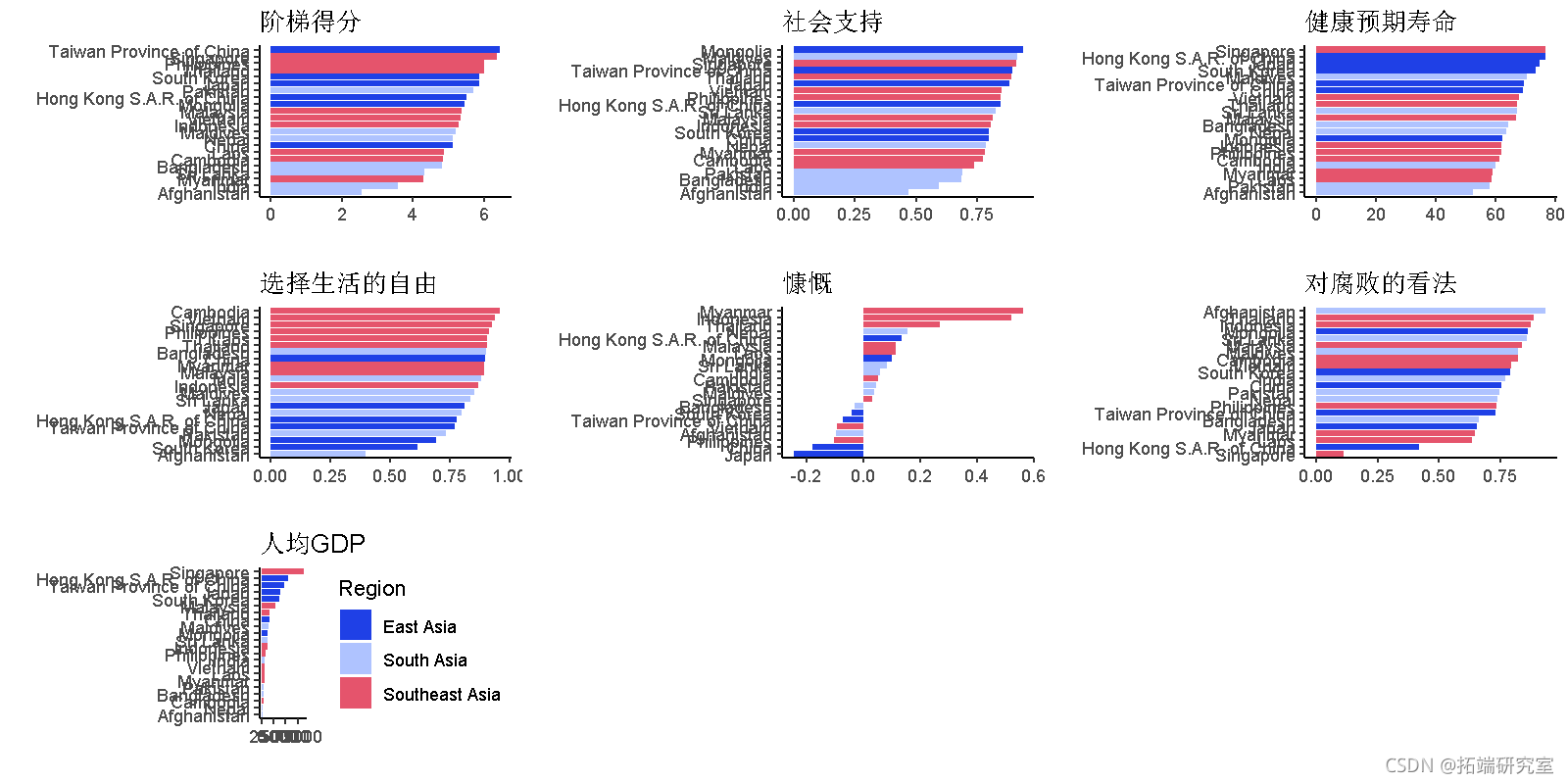
- 东亚国家的阶梯得分较高,预期寿命健康,人均GDP较高且慷慨度较低。
- 南亚国家的阶梯得分,社会支持,健康的预期寿命和人均GDP往往较低。
- 东南亚国家往往有很高的自由度,可以选择生活和慷慨解囊。
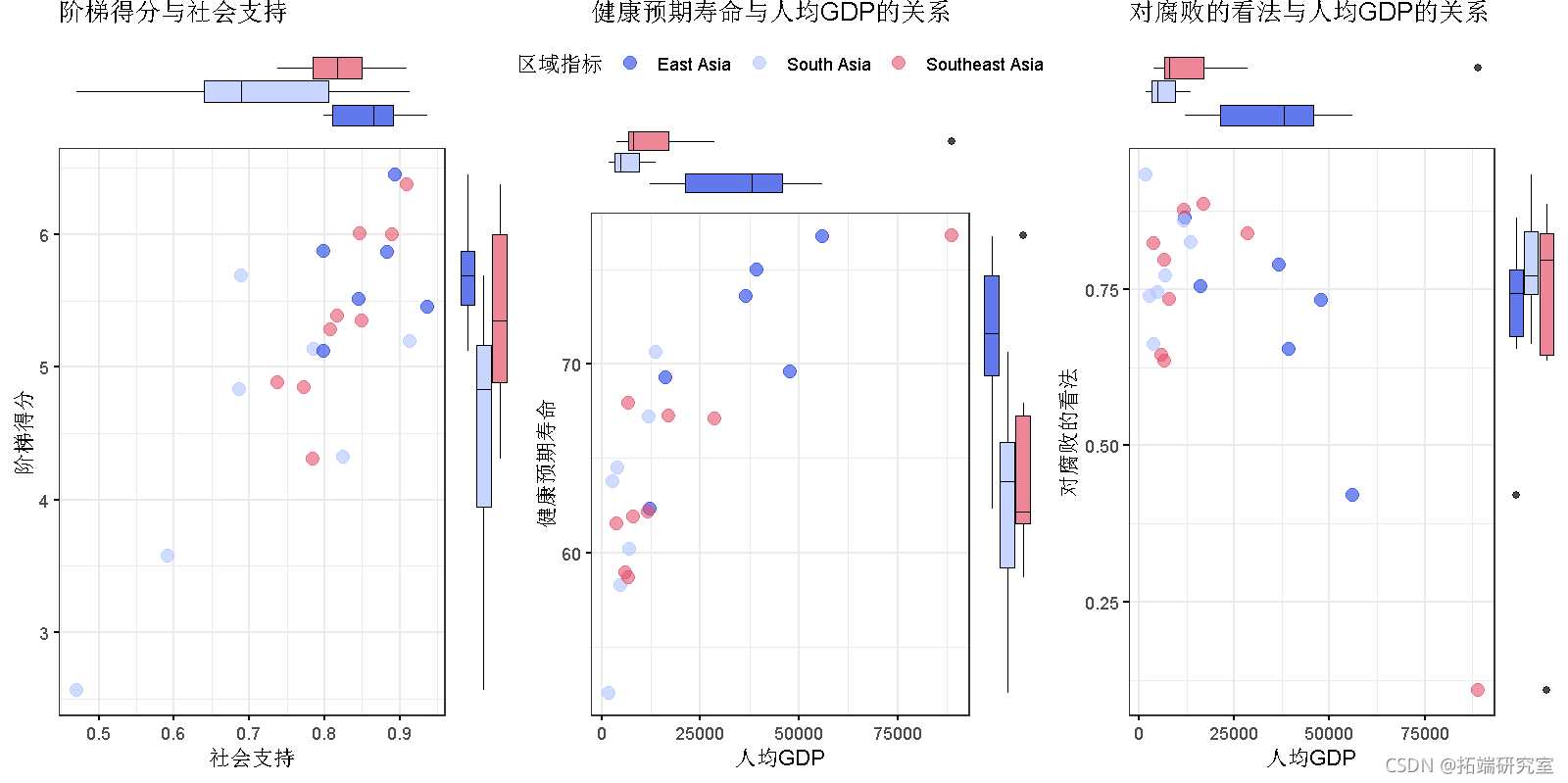
scterhst( aia, x = "社会支持", y = "阶梯得分", clor = "区域指标" titl = "阶梯得分与社会支持" )
随时关注您喜欢的主题
- 南亚的社会支持中位数,阶梯得分和人均GDP最低。
- 东亚的社会支持中位数,阶梯得分,人均GDP和健康的预期寿命最高。
- 东南亚的平均健康寿命中位数最低,对腐败的中位数最高。
- 东南亚的人均GDP很高,预期寿命健康,对腐败的看法也很低(新加坡)。
- 东亚有离群点样本对政府的了解低(香港)。
聚类分析
这些国家会属于不同的群体吗?在本节中,我们将使用聚类(一种无监督的学习方法,该方法基于相似性对对象进行分组)来找到国家组,其中组内的国家相似。我将使用两种方法进行聚类:分层聚类和K-Means聚类。首先,我们如何识别这些群体?衡量对象之间相似性的一种方法是测量对象之间的数学距离。一种常见的距离度量是欧几里得距离。
欧氏距离
我们将使用欧几里得距离找到彼此最相似的国家,并将它们分组在一起。
aply(z,2,mean) # 计算列的平均值 aply(z,2,sd) # 计算列的标准差 scale(z,ceter=means,scae=sds) # 标准化 # 计算距离矩阵 dsae = dit(nor) # 计算欧几里得的距离
欧几里得距离矩阵为:
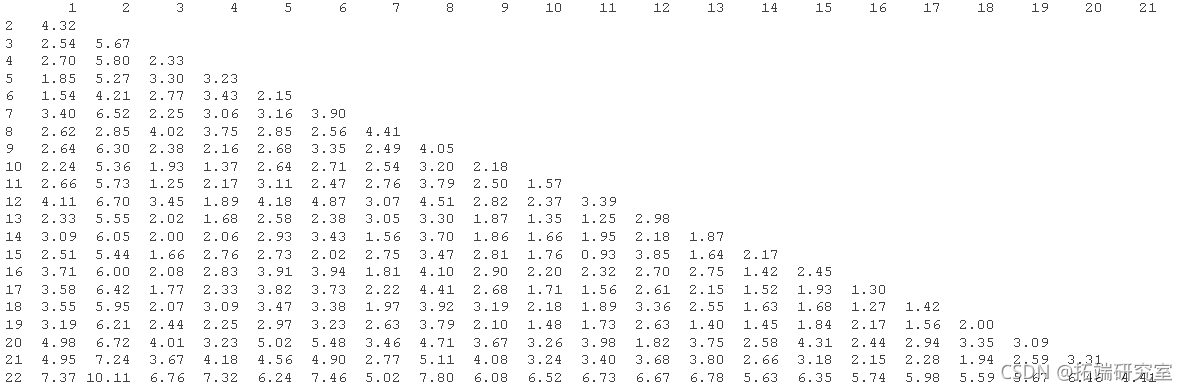
- 似乎国家2(新加坡)和国家22(阿富汗)彼此最不相似。
- 15国(中国)和11国(越南)彼此最相似。
我们如何选择最佳聚类数?
肘法
for (i in 2:20) ws<- sum(kmens(nr, cetrs=i)$wthns)
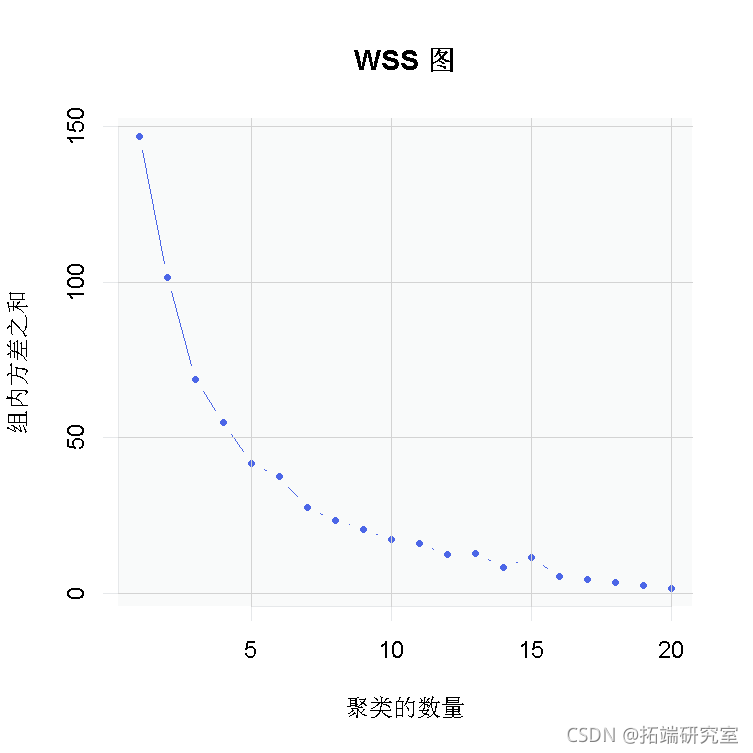
我们的目标是减少聚类内部的变异性,以便将相似的对象分组在一起,并增加聚类之间的变异性,以使相异的对象相距甚远。WSS(在组平方和内),它在聚类变化内进行度量,
在WSS图中,聚类数位于x轴上,而WSS位于y轴上。高的WSS值意味着聚类中的变化很大,反之亦然。我们看到,在1、2和3个聚类之后,WSS的下降很大。但是,在4个聚类之后,WSS的下降很小。因此,聚类的最佳数目为k = 4(曲线的弯头)。
K均值聚类
k均值算法如下所示:
- 为每个观测值随机分配一个从1到K的数字,这些数字用作观测值的初始聚类分配。
- 迭代直到聚类分配停止更改:
(a)对于K个聚类中的每一个,计算聚类质心。
(b)将每个观测值分配给质心最接近的聚类(使用欧几里得距离定义)。
k均值聚类的结果是:
聚类成员和结果
#聚类成员 asa$Cuter <- c$luser

聚类图在散点图中绘制k均值聚类和前两个主成分(维度1和2)。
clstr(lstdaa = nr, cluter = cluser,col=ola), theme = hme_lsic()) +
title("K-Means聚类图")
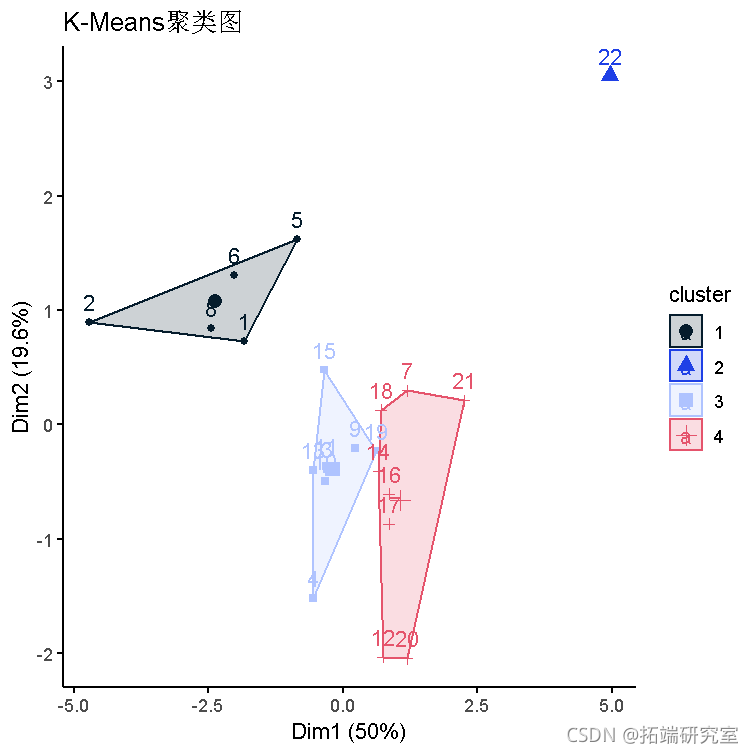
- 聚类之间没有重叠。
- 聚类2与其他聚类之间存在很多分隔。
- 聚类1、3和4之间的间隔较小。
- 前两个组成部分解释了点变异的70%。

- 聚类1有2个国家,其聚类平方和之内很小(在聚类变异性内)。
- 聚类2有1个国家。
- 具有14个国家/地区的第3组在类内变异性中最高。
- 聚类4有5个国家,在聚类变异性中排名第二。
- 聚类平方和与平方和之比为61.6%,非常合适。
这四个聚类的标准平均值是:
long <- melt(t(agreate(nor, ) plot(long,roup = cluster)+point(se=3)
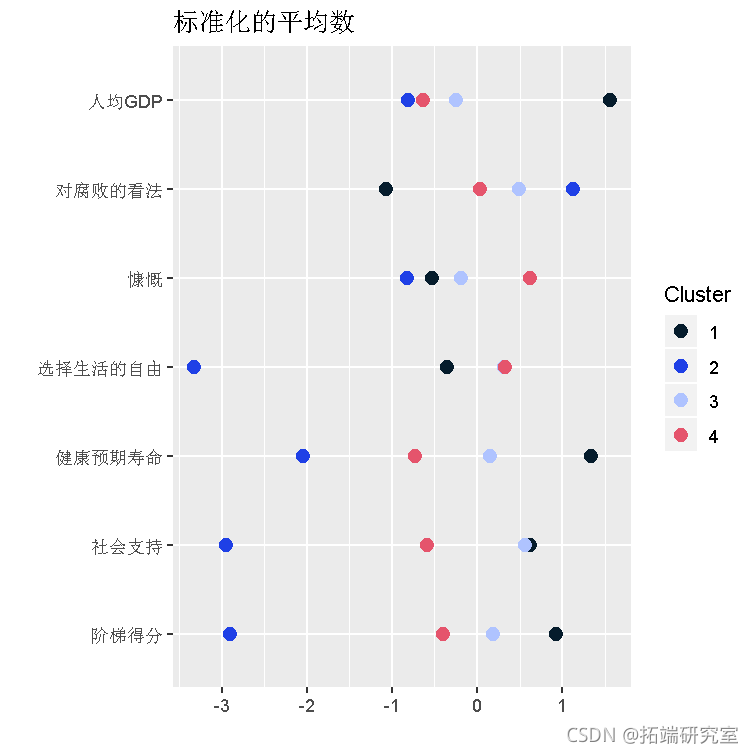
自由选择生活,社会支持和阶梯得分之间的差异很大。这些变量似乎对聚类形成贡献最大。
回想一下,聚类成员资格为:
类别1:印度尼西亚,缅甸
第二类:阿富汗
类别3:菲律宾,泰国,巴基斯坦,蒙古,马来西亚,越南,马尔代夫,尼泊尔,中国,老挝,柬埔寨,孟加拉国,斯里兰卡,印度
第4组:中国台湾地区,新加坡,韩国,日本,中国香港特别行政区
相对于其他聚类:
聚类1的特点是
- 很高:慷慨
- 高:自由选择生活
- 一般:人均GDP,对腐败的看法,慷慨,健康的预期寿命,社会支持,阶梯得分
聚类2的特点是
- 高:对腐败的看法
- 低:人均国内生产总值,慷慨
- 非常低:自由选择生活,健康的预期寿命,社会支持,阶梯得分
聚类3的特点是
- 高:自由选择生活
- 一般:人均GDP,对腐败的看法,慷慨,健康的预期寿命,社会支持,阶梯得分
聚类4的特点是
- 很高:人均GDP,预期寿命健康
- 高:社会支持,阶梯得分
- 一般:自由选择生活
- 低:慷慨
- 极低:对腐败的看法
轮廓图
我们使用轮廓图来查看每个国家在其聚类中的状况。轮廓宽度衡量一个聚类中每个观测值相对于其他聚类的接近程度。较高的轮廓宽度表示该观测值很好地聚类,而接近0的值表示该观测值在两个聚类之间匹配,而负值表示该观测值在错误的聚类中。
plt(soette((cluser), diace), mn = "轮廓系数图")
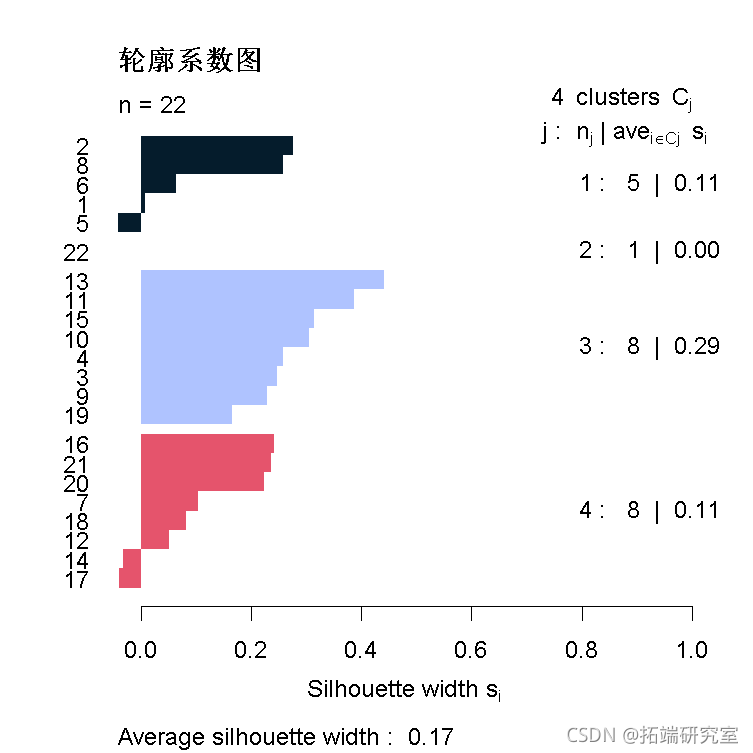
- 大多数国家似乎都非常好。
- 第3组中的国家4(泰国)和第4组中的国家5(韩国)的轮廓宽度非常低。
层次聚类
分层聚类将组映射到称为树状图的层次结构中。分层聚类算法如下所示:
- 从n个观察值和所有成对不相似性的度量(例如欧几里得距离)开始。将每个观察值视为自己的聚类。
(a)检查i个聚类之间所有成对的聚类间差异,并找出最相似的一对聚类。加入这两个聚类。这两个簇之间的差异表明它们在树状图中的高度。
(b)计算其余聚类之间的新的成对聚类间差异。对于分层聚类,我们在聚类之间使用距离函数,称为链接函数。不同类型的链接:
- 完全(最大聚类间差异):计算聚类1中的观测值与聚类2中的观测值之间的所有成对差异,并记录这些差异中最大的一个。
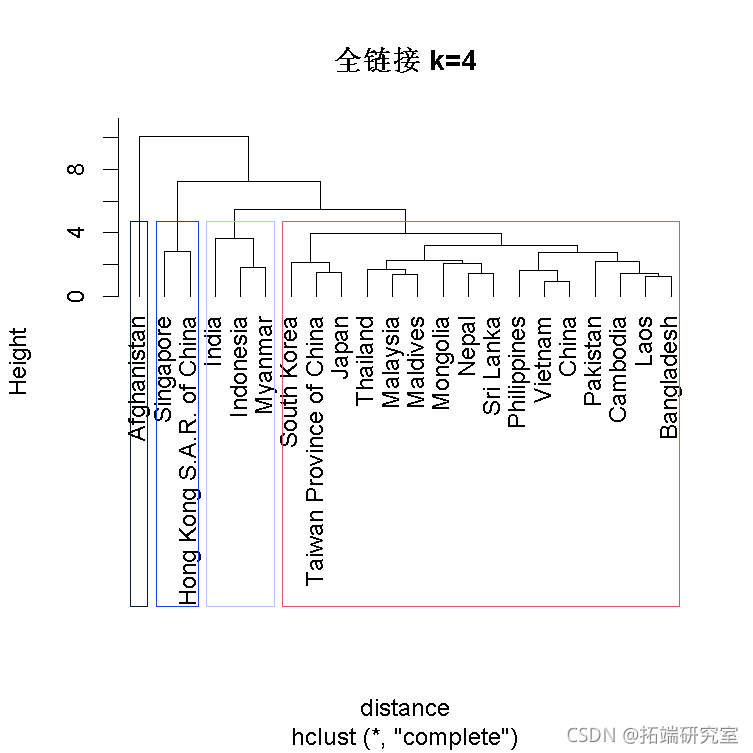
plt(aslus.c,laes=国家名称,min='全链接 k=4', hang=-1) rct.clut(whasi.hclusc, k=4)
- 平均值(均值聚类间差异):计算聚类1中的观测值与聚类2中的观测值之间的所有成对差异,并记录这些差异的平均值。
全链接
下面的树状图显示了使用全链接的聚类层次结构。
custr(ist(dta = or, cuse = mer.a), ghe = teelsic)) +
title("全链接 lusterPlot")
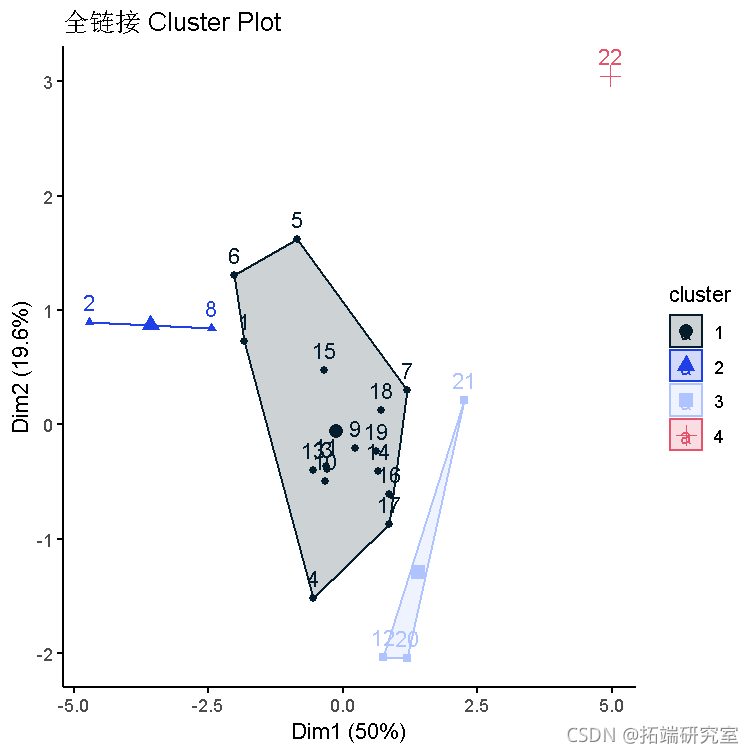
- 聚类1有16个国家。
- 聚类2有2个国家。
- 聚类3有3个国家。
- 聚类4有1个国家。
- 聚类4和其他聚类之间有很多间隔。
- 聚类1、2和3之间的间隔较小。
- 聚类1中的变异性似乎很大。
轮廓图
plot(sloett(curee(asiahluc, 4), di), col min = "全链接 轮廓系数图")
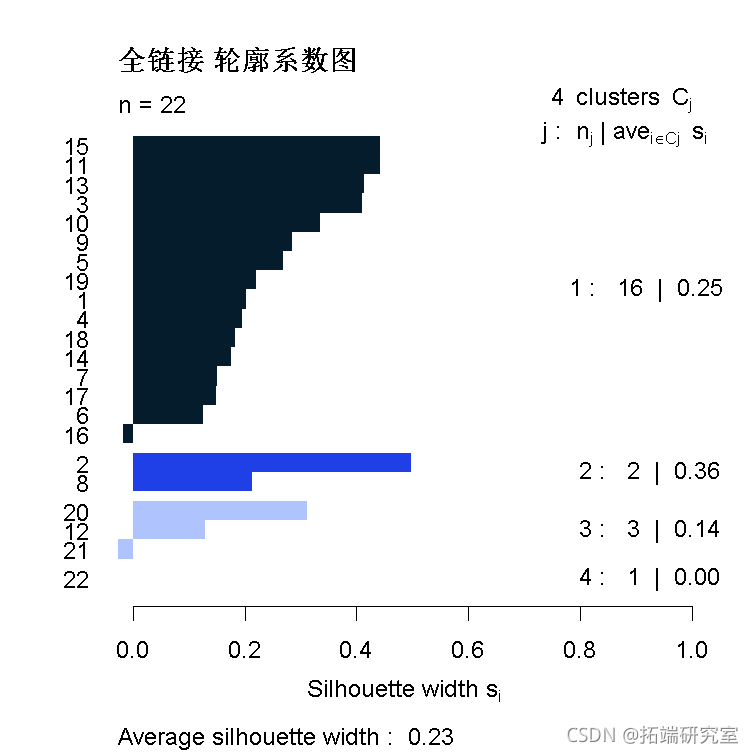
大多数国家似乎都非常好。
- 16国(老挝)似乎是第1组的异常值。
- 21国(印度)似乎是第3组的异常值。
平均链接
下面的树状图显示了使用平均链接的聚类层次。
plt(s.hut.,abls=国家名称,min='平均链接 k=4', hag=-1) rec(hsth_asa.lus.a, k= boder)
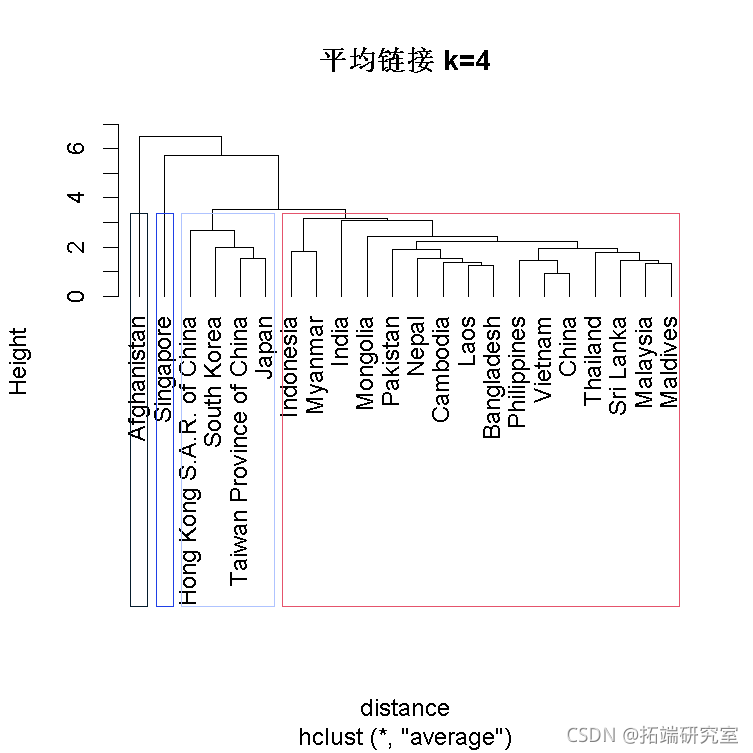
- 聚类1有4个国家。
- 聚类2有1个国家。
- 聚类3有16个国家。
- 聚类4有1个国家。
- 使用平均链接的聚类之间的变异性似乎大于全链接的变异性。
custr(ist(dta = or, cuse = mer.a), ghe = teelsic)) +
title("平均链接 lusterPlot")
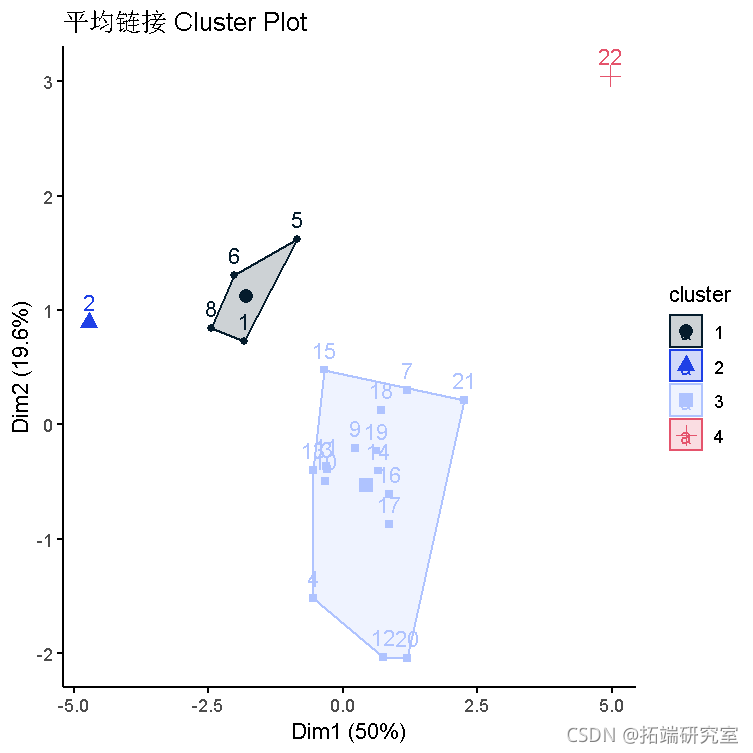
轮廓图
plt(sltte(ctee(sia.lust, 4), istce), cl=cl\[:5\], min = "平均链接 轮廓系数图")
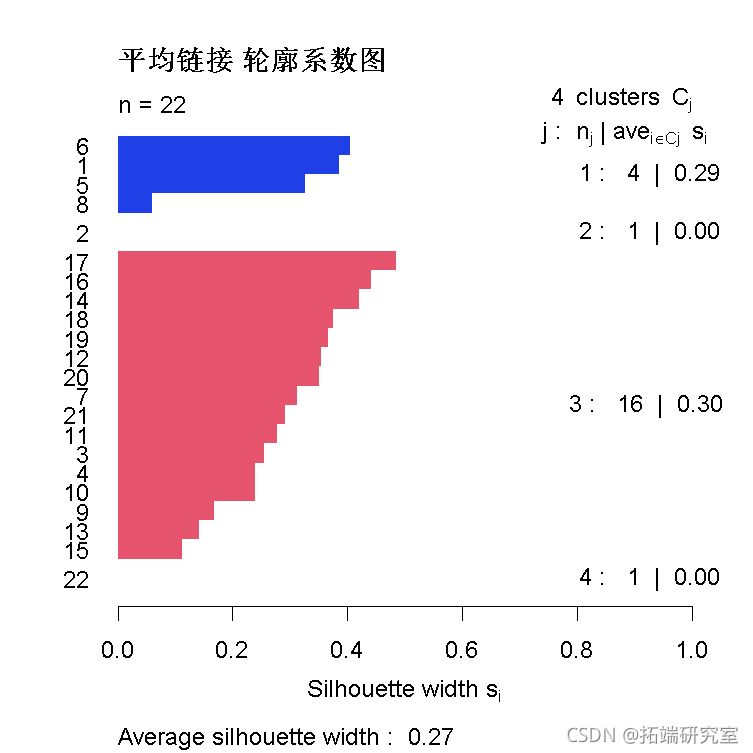
- 大多数国家似乎都非常好。
- 第1组中的8地区(香港)的轮廓宽度非常小。
讨论
k均值,全链接和平均链接的平均轮廓宽度分别为0.26、0.23和0.27。在全链接中,聚类之间的距离小于k均值和平均链接之间的距离,并且两个国家不太适合它们的聚类。因此,k均值和平均链接方法似乎比全链接具有更好的拟合度。比较k均值,全链接和平均链接,所有方法都与阿富汗匹配,成为其自己的聚类。但是,每种方法的聚类成员资格有所不同。例如,在k均值和全链接中,印度尼西亚和缅甸与大多数南亚和东南亚国家不在同一聚类中,而印度尼西亚和缅甸与在平均链接中的国家在同一聚类中。
K-means和分层聚类都产生了相当好的聚类结果。在使用大型数据集和解释聚类结果时,K-means有一个优势。K-means的缺点是它需要在开始时指定数字数据和聚类的数量。另外,由于初始聚类分配在开始时是随机的,当你再次运行该算法时,聚类结果是不同的。另一方面,分层聚类对数字和分类数据都有效,不需要先指定聚类的数量,而且每次运行算法都会得到相同的结果。它还能产生树状图,这对帮助你理解数据的结构和挑选聚类的数量很有用。然而,一些缺点是,对于大数据来说,它没有k-means那么有效,而且从树状图中确定聚类的数量变得很困难。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测
SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测 Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别
Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别 Python、Amos汽车用户满意度数据分析:BERT情感分析、CatBoost、XGBoost、LightGBM、ACSI、GMM聚类、SHAP解释、MICE插补、PCA降维、熵权法
Python、Amos汽车用户满意度数据分析:BERT情感分析、CatBoost、XGBoost、LightGBM、ACSI、GMM聚类、SHAP解释、MICE插补、PCA降维、熵权法



