当ARIMA模型包括其它时间序列作为输入变量时,被称为传递函数模型(transfer function model)、多变量时间序列模型(multivariate time series model)、ARIMAX模型或Box-Tiao模型。
传递函数模型是ARIMA模型的自然推广,Pankratz统称这种包含其它时间序列作为输入变量的ARIMA模型为动态回归。
用于预测的 Arima
加载相关包和数据
ARMA将当前和过去建立一种线性关系，从而提炼出白噪声这样的期望为零性质很好的误差序列，继而研究用于表征各时间点关系的(偏)自相关系数等一系列指标，并使用检验统计量做显著性检验，以验证当前模型反映信息提炼的效果。
LSTM作为RNN的一种形式，或者往更大范围说是一种神经网络模型，它也是一种信息提炼，或者可以理解成信息流过滤机制，针对时序数据也是将当前和过去建立一种线性关系，在神经网络各层间通过感知机激活传递有价值的信息。
一个是信息提炼，一个是信息过滤；一个是以白噪声纯随机序列作为终结，一个是以损失函数收敛作为终结，殊途同归啊！其背后的核心数学原理都是空间变换【将实际样本空间的点数据，经过一系列几何变换（神经网络中的W权重矩阵，ARMA中的自回归系数或特征根）】和收敛性【挖掘样本数据中的规律，无论用何种方式其充要条件是收敛（神经网络中的loss收敛，ARMA中的自协方差及残差方差收敛）】。
bata<-read.csv colnames(bata) bata<-bata\[order(as.Date,\] bata<-bata\[order(as.Date,\] bata$workda<-as.factor head(bata)
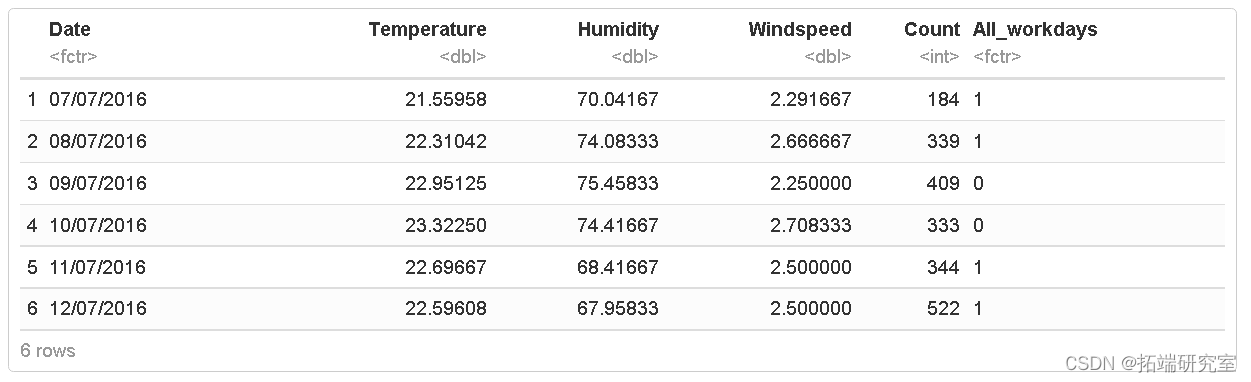
将数据划分为训练集和测试集
#ARIMA 编程开始 ## 75% 的样本量 smsize <- floor(0.95 * nrow) print(smze)
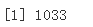
## 设置种子可重现 set.seed(123) traid <- sample trn <- bata\[1:smize, \] tet <- baata\[smp_size+1:nrow, \] tet<-na.omit
创建预测矩阵
xreg <- cbind(as_workday=model.matrix,
Temp,
Humid,
Winds
)
# 删除截距
xg <- xg\[,-1\]
# 重命名列
colnames<- c("Aldays","Tep","Humty","Wined")
#为测试数据创建相同的
xrg1 <- cbind
# 删除截距
xreg1 <- xre1\[,-1\]
# 重命名列
colnames <- c("Aays","Te","uiiy","Wnsed")
为 arima 预测的训练数据创建时间序列变量
Cont <- ts
推论：由于数据是每天的，频率为 365，开始日期为 2016-7-7
用季节性拟合 ARIMA 模型
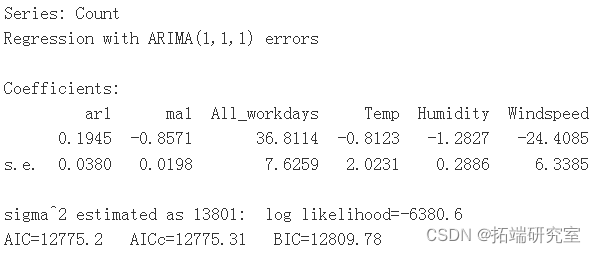
Fo_aes<-forecast
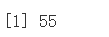
计算测试数据集 MSE
mean((tt - Finlues)^2)
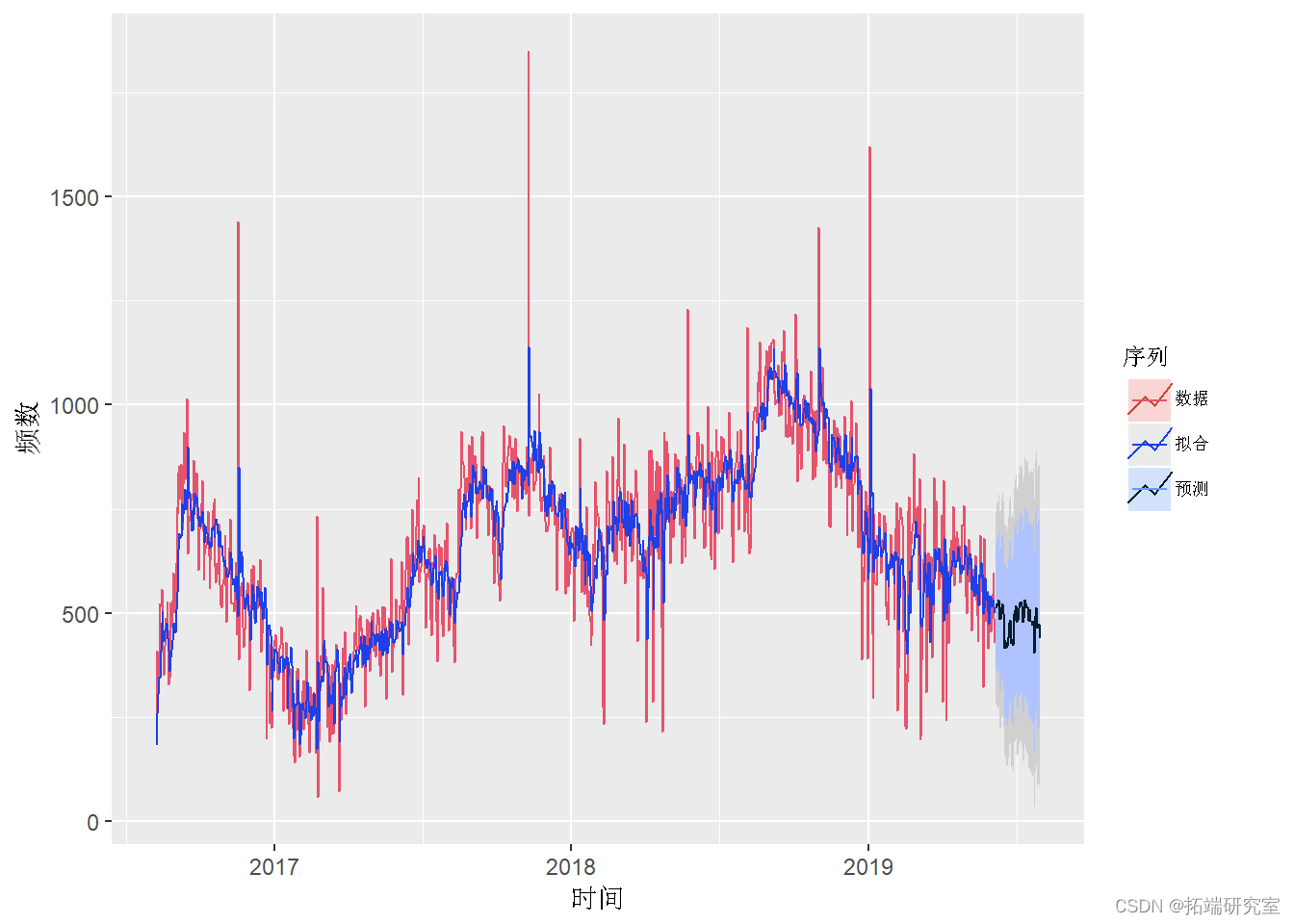
在去除季节性之前绘制预测值
library(ggplot2)
随时关注您喜欢的主题
无季节性拟合 ARIMA
去季节性数据集和绘图
decata = decompos
### 查找去除季节数据的 ARIMAX 模型
moesea
Foecs<-forecast
去除季节性后绘制预测值
library(ggplot2) plot(Co, series="Data") + autolayer+ autolayer
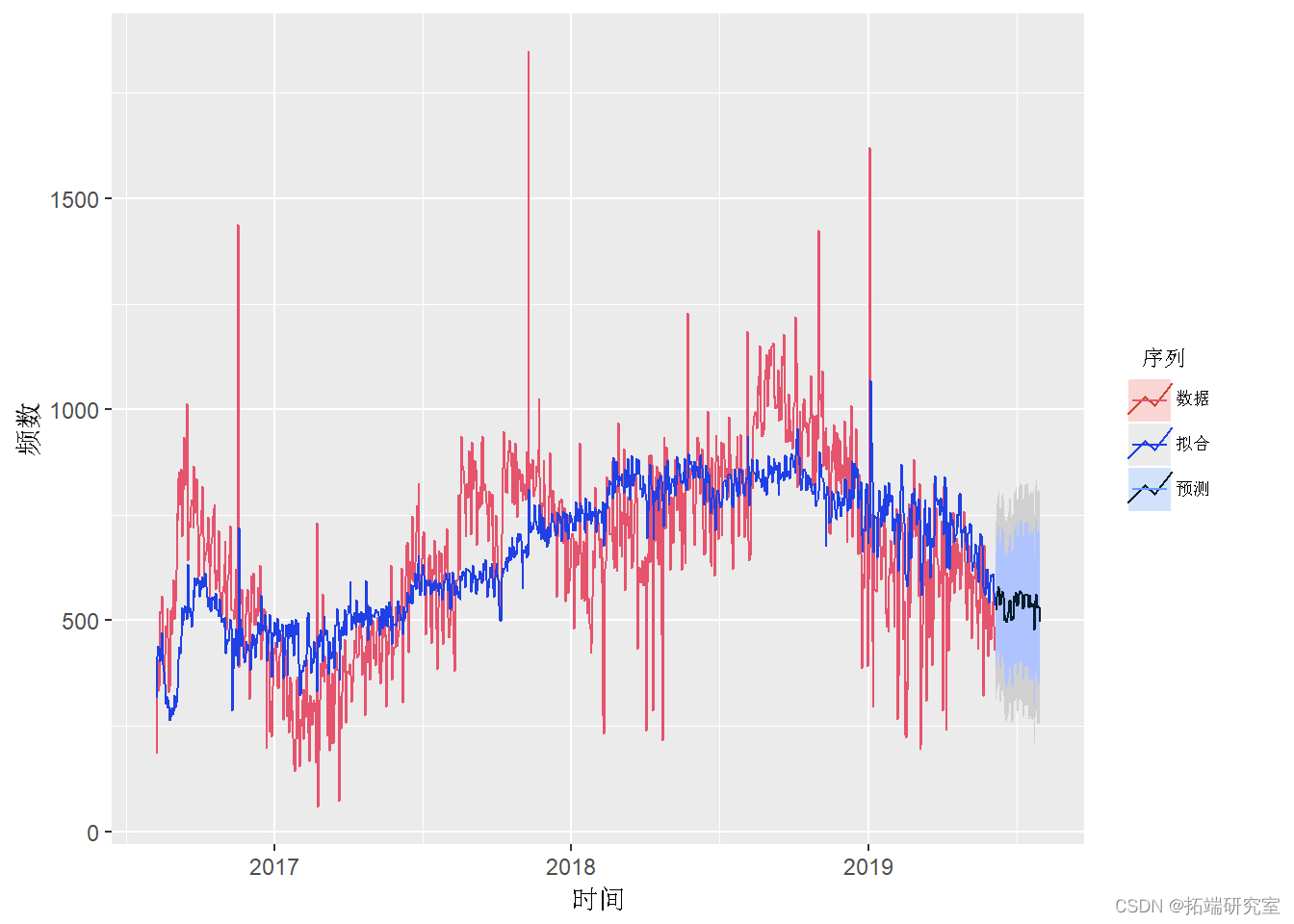
均方误差分量
mean((tount - Fis_des)^2)
通过采用滞后变量的输出以及滞后 1,2 的输入进行动态回归
x<-train\[order,\] ti_ag <- x %>% mutate x1<-test testg <- x1 %>% mutate
使用动态滞后变量的 OLS 回归
mlm <- lm
推论：仅保留 P 值 <0.05 的重要变量并删除其他变量
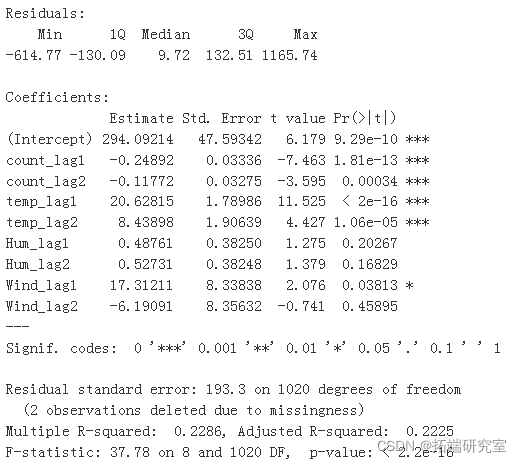
仅保留重要变量的情况下重新创建 OLS 回归
Myal <-lm summary(Myal )
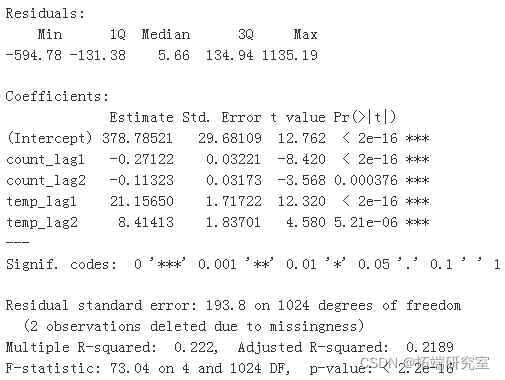
在测试数据上预测相同以计算 MSE
prynm<-predict # 动态回归的均方误差 mean((teunt - tPrecd)^2)
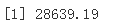
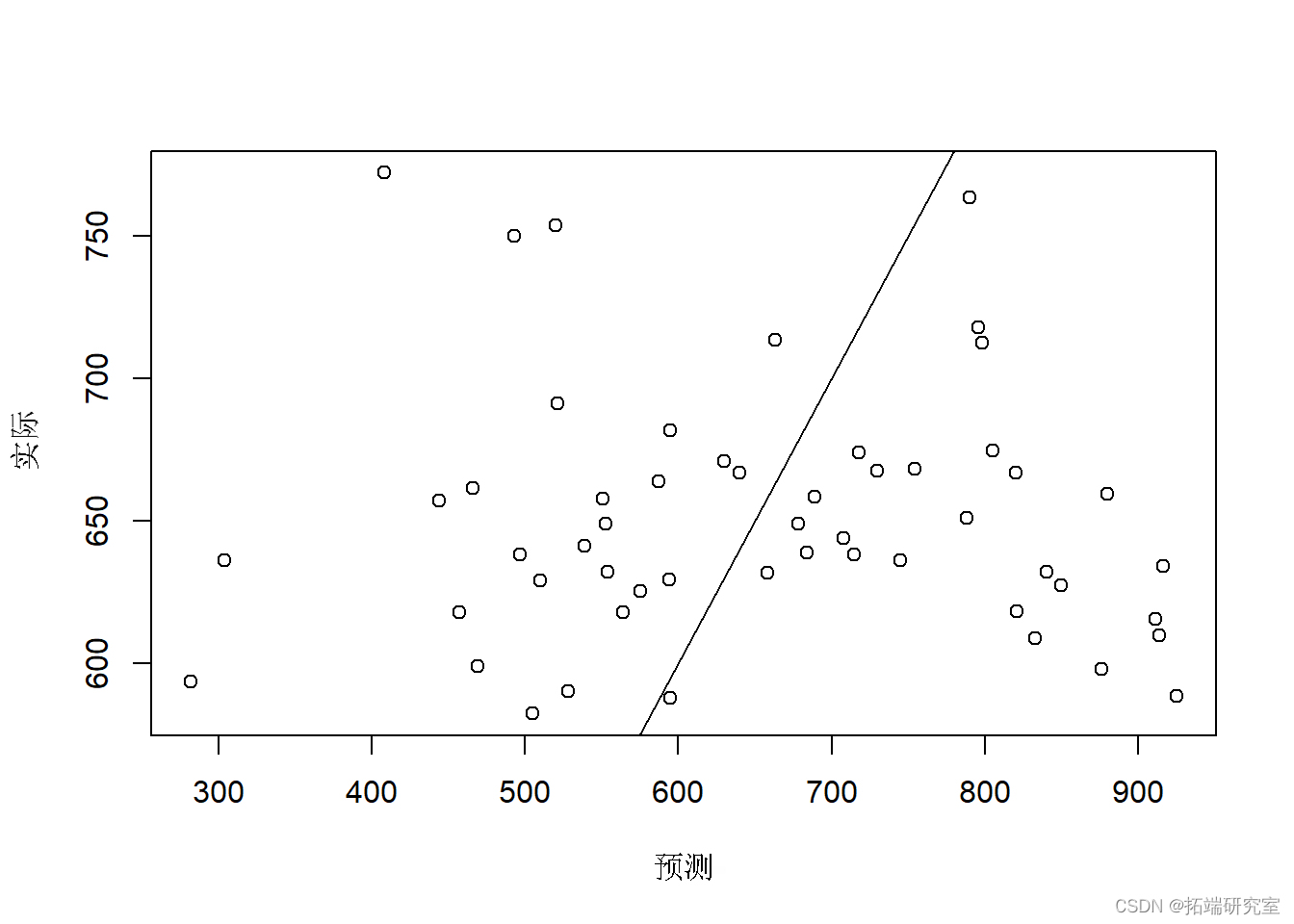
绘制预测与实际
plot abline
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】R语言支持向量回归SVR预测水位实例讲解|附代码数据
数据分享|R语言Python机器学习预测4案例合集：众筹平台、机票折扣、糖尿病患者、员工满意度
R语言用随机森林模型的酒店收入和产量预测误差分析
