
本文描述了R语言中马尔克夫转换模型的分析过程。
首先,对模拟数据集进行详细建模。接下来,将马尔可夫转换模型拟合到具有离散响应变量的真实数据集。用于验证对这些数据集建模的不同方法。
可下载资源
模拟实例
示例数据是一个模拟数据集,用于展示如何检测两种不同模式的存在:一种模式中的响应变量高度相关,另一种模式中的响应仅取决于外生变量x。自相关观测值的区间为1到100、151到180 和251到300。每种方案的真实模型为: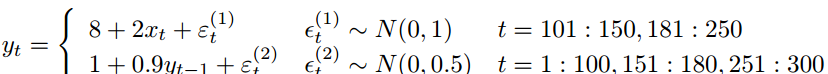
1. 马尔可夫链
设表示随机变量X在离散时间t时刻的取值。若该变量随时间变化的转移概率仅依赖于它的当前值,即:
也就是时候状态转移概率指依赖于前一个状态,称这个变量为马尔可夫变量,其中 为随机变量X可能的状态,这个性质称为马尔可夫性质,具有马尔可夫性质的随机过程称为马尔可夫过程。
马尔可夫链是满足马尔可夫性质的随机过程,指在一段时间内随机变量X的取值序列()满足上述性质
2、转移概率
马尔可夫链是通过转移概率定义的,转移概率指随机变量从一个时刻到下一个时刻,从状态转移到状态
的概率:
记表示变量X在时刻t的取值为
的概率,则随机变量X在时刻t+1的取值为
的概率为:
假设状态的数目为n,则:
3 马尔可夫链的平稳分布
-
1.周期性:即经过有限次的状态转移,又回到了自身
-
马尔可夫模型如下所示:
-
不可约:两个状态之间的转移
可见状态之间没有转换概率,但是隐含态和可见态之间存在一个概率叫做输出概率。
上述概率转移公式就是表示模型中状态转移的情况。
如果一个马尔可夫过程既没有周期性,又不可约,则称为各态遍历的。
对于一个各态遍历的马尔可夫过程,无论初始值取何值,随着转移次数的增多,随机变量的取值分布最终都收敛到唯一的平稳分布
:
其中为转移概率矩阵。
图1中的曲线表明,在不存在自相关的区间中,响应变量y具有与协变量x相似的行为。拟合线性模型以研究协变量x如何解释变量响应y。
> summary(mod)
Call:
lm(formula = y ~ x, data = example)
Residuals:
Min 1Q Median 3Q Max
-2.8998 -0.8429 -0.0427 0.7420 4.0337
> plot(ts(example))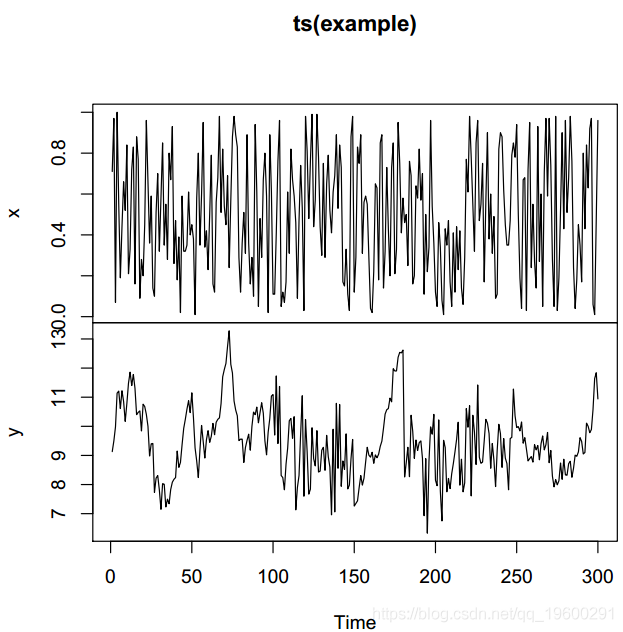
图1:模拟数据,y变量是响应变量
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.0486 0.1398 64.709 < 2e-16 ***
x 0.8235 0.2423 3.398 0.00077 ***
Residual standard error: 1.208 on 298 degrees of freedom
Multiple R-squared: 0.03731, Adjusted R-squared: 0.03408
F-statistic: 11.55 on 1 and 298 DF, p-value: 0.0007701
协变量确实很重要,但是模型解释的数据行为非常糟糕。图1中的线性模型残差图表明,它们的自相关很强。残差的诊断图(图2)确认它们似乎不是白噪声,并且具有自相关关系。接下来,将自回归马尔可夫转换模型(MSM-AR)拟合到数据。
自回归部分设置为1。为了指示所有参数在两个周期中都可以不同,将转换参数(sw)设置为具有四个分量的矢量。拟合线性模型时的最后一个值称为残差。
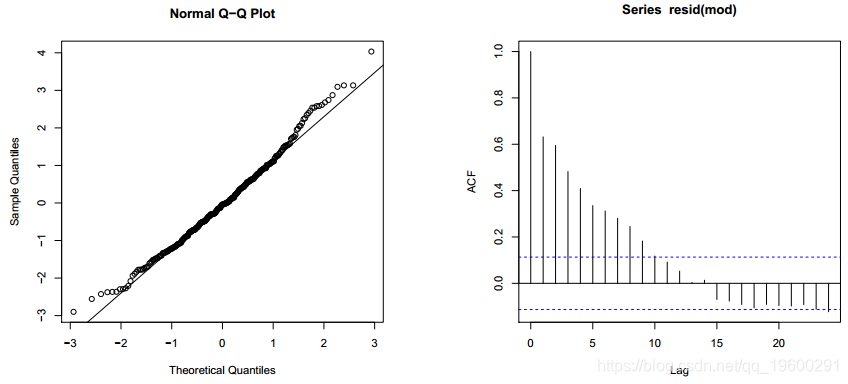
标准偏差。有一些选项可控制估算过程,例如用于指示是否完成了过程并行化的逻辑参数。
Markov Switching Model
AIC BIC logLik
637.0736 693.479 -312.5368
Coefficients:
Regime 1
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 0.8417 0.3025 2.7825 0.005394 **
x(S) -0.0533 0.1340 -0.3978 0.690778
y_1(S) 0.9208 0.0306 30.0915 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5034675
Multiple R-squared: 0.8375
Standardized Residuals:
Min Q1 Med Q3 Max
-1.5153666657 -0.0906543311 0.0001873641 0.1656717256 1.2020898986
Regime 2
--------- Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 8.6393 0.7244 11.9261 < 2.2e-16 ***
x(S) 1.8771 0.3107 6.0415 1.527e-09 ***
y_1(S) -0.0569 0.0797 -0.7139 0.4753
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9339683
Multiple R-squared: 0.2408
Standardized Residuals:
Min Q1 Med Q3 Max
-2.31102193 -0.03317756 0.01034139 0.04509105 2.85245598
Transition probabilities:
Regime 1 Regime 2
Regime 1 0.98499728 0.02290884
Regime 2 0.01500272 0.97709116模型mod.mswm具有协方差x非常显着的状态,而在其他情况下,自相关变量也非常重要。两者的R平方均具有较高的值。最后,转移概率矩阵具有较高的值,这表明很难从接通状态更改为另一个状态。该模型可以完美地检测每个状态的周期。残差看起来像是白噪声,它们适合正态分布。而且,自相关消失了。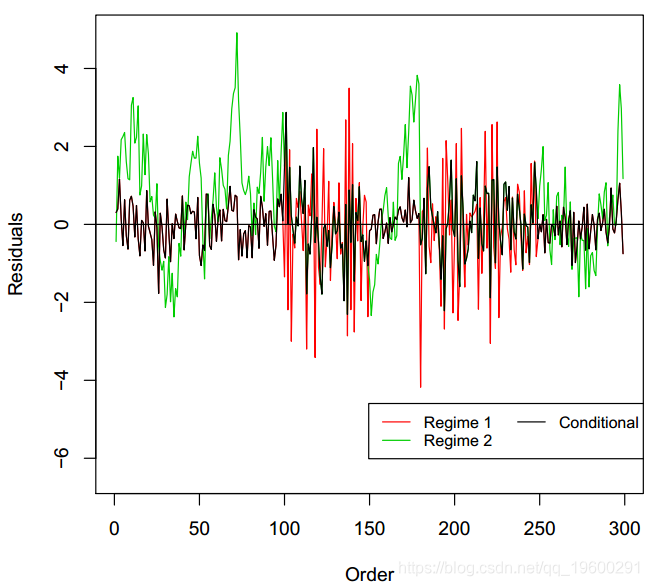
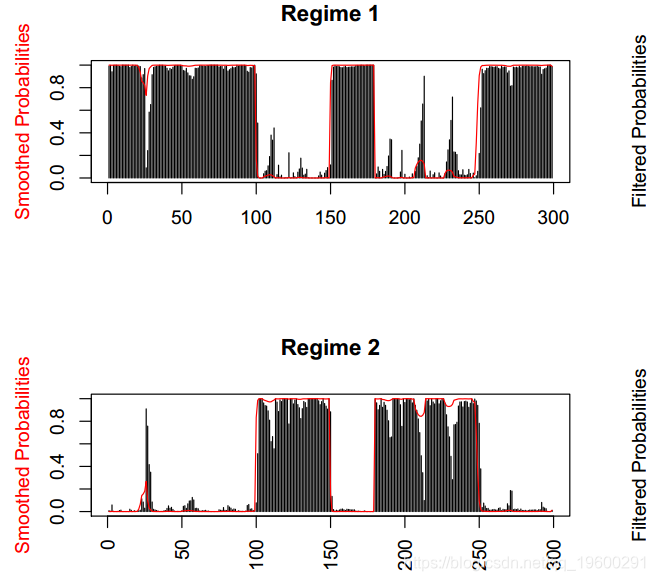
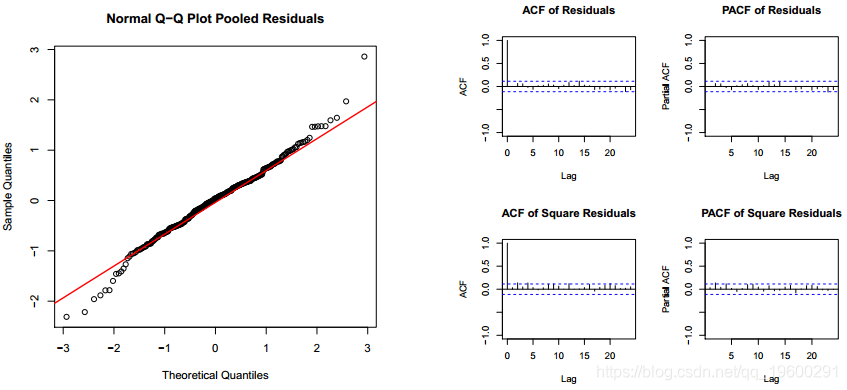
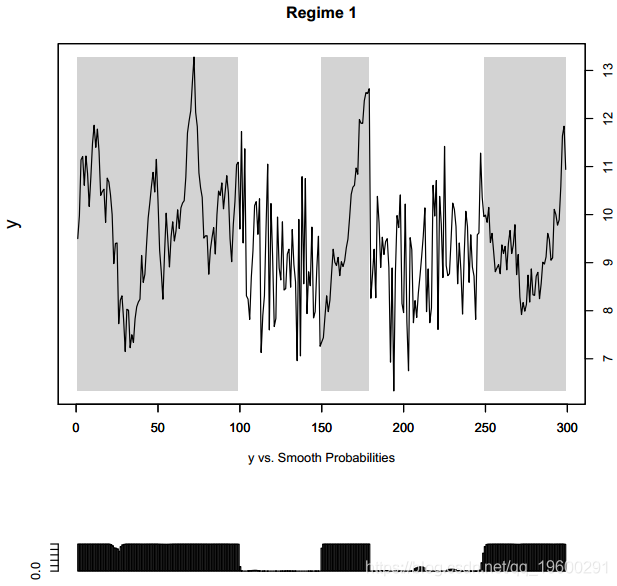
图形显示已完美检测到每个方案的周期。
> plot(mod.mswm,expl="x")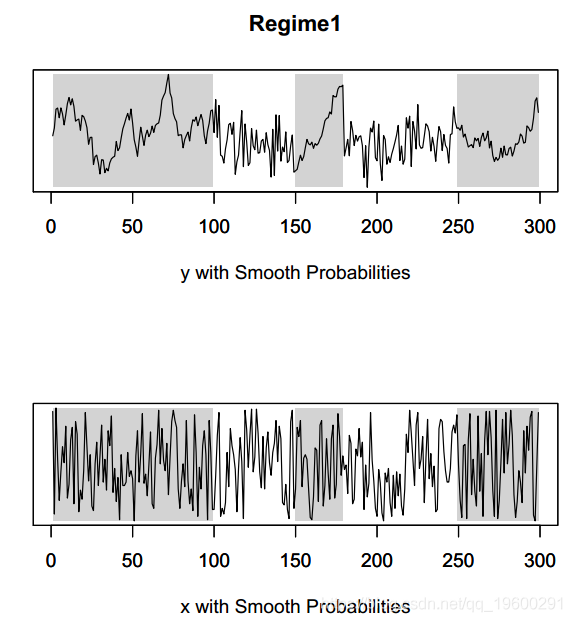
交通事故
交通数据包含2010年西班牙交通事故的每日人数,平均每日温度和每日降水量。该数据的目的是研究死亡人数与气候条件之间的关系。由于在周末和工作日变量之间存在不同的行为,因此我们说明了在这种情况下使用广义马尔科夫转换模型的情况。
在此示例中,响应变量是计数变量。因此,我们拟合了泊松广义线性模型。
> summary(model)
Call:
glm(formula = NDead ~ Temp + Prec, family = "poisson", data = traffic)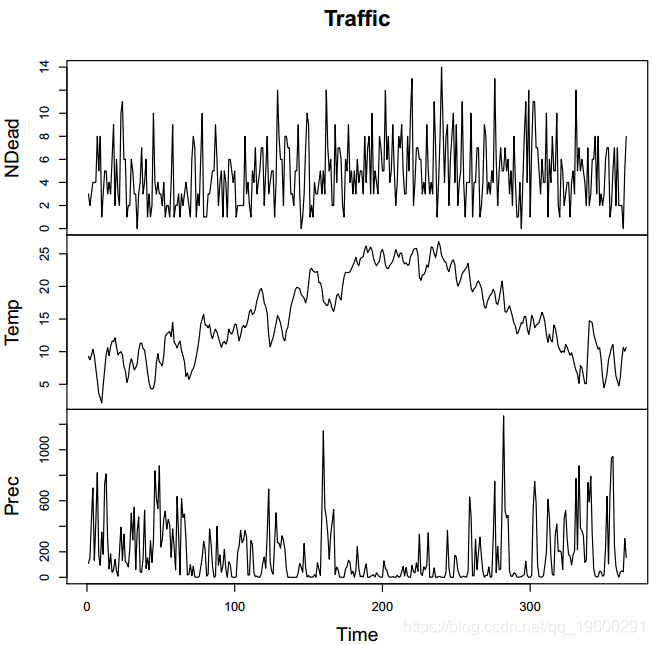
Deviance Residuals:
Min 1Q Median 3Q Max
-3.1571 -1.0676 -0.2119 0.8080 3.0629
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.1638122 0.0808726 14.391 < 2e-16 ***
Temp 0.0225513 0.0041964 5.374 7.7e-08 ***
Prec 0.0002187 0.0001113 1.964 0.0495 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 597.03 on 364 degrees of freedom
Residual deviance: 567.94 on 362 degrees of freedom
AIC: 1755.9
Number of Fisher Scoring iterations: 5
下一步,使用拟合马尔可夫转换模型。为了适应广义马尔可夫转换模型,必须包含族参数,而且glm没有标准偏差参数,因此sw参数不包含其切换参数。
>
Markov Switching Model
AIC BIC logLik
1713.878 1772.676 -850.9388
Coefficients:
Regime 1
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 0.7649 0.1755 4.3584 1.31e-05 ***
Temp(S) 0.0288 0.0082 3.5122 0.0004444 ***
Prec(S) 0.0002 0.0002 1.0000 0.3173105
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Regime 2
---------
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 1.5659 0.1576 9.9359 < 2e-16 ***
Temp(S) 0.0194 0.0080 2.4250 0.01531 *
Prec(S) 0.0004 0.0002 2.0000 0.04550 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Transition probabilities:
Regime 1 Regime 2
Regime 1 0.7287732 0.4913893
Regime 2 0.2712268 0.5086107两种状态都有显着的协变量,但降水协变量仅在这两种状态之一中是显着的。
Aproximate intervals for the coefficients. Level= 0.95
(Intercept):
Lower Estimation Upper
Regime 1 0.4208398 0.7648733 1.108907
Regime 2 1.2569375 1.5658582 1.874779
Temp:
Lower Estimation Upper
Regime 1 0.012728077 0.02884933 0.04497059
Regime 2 0.003708441 0.01939770 0.03508696
Prec:
Lower Estimation Upper
Regime 1 -1.832783e-04 0.0001846684 0.0005526152
Regime 2 -4.808567e-05 0.0004106061 0.0008692979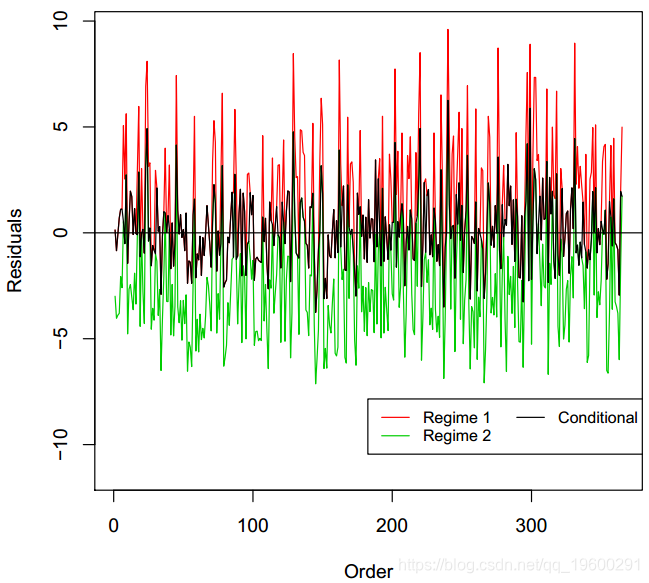
由于模型是通用线性模型的扩展,因此从类对象计算出图中的Pearson残差。该残差有白噪声的经典结构。残差不是自相关的,但它们与正态分布不太吻合。但是,Pearson残差的正态性不是广义线性模型验证的关键条件。
> plot(m1,which=2)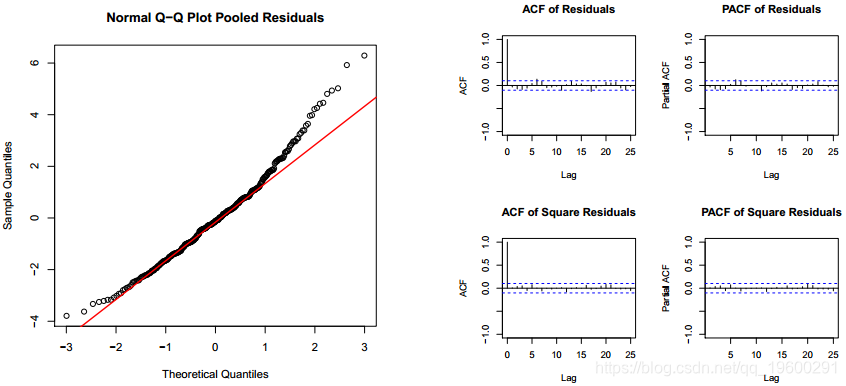
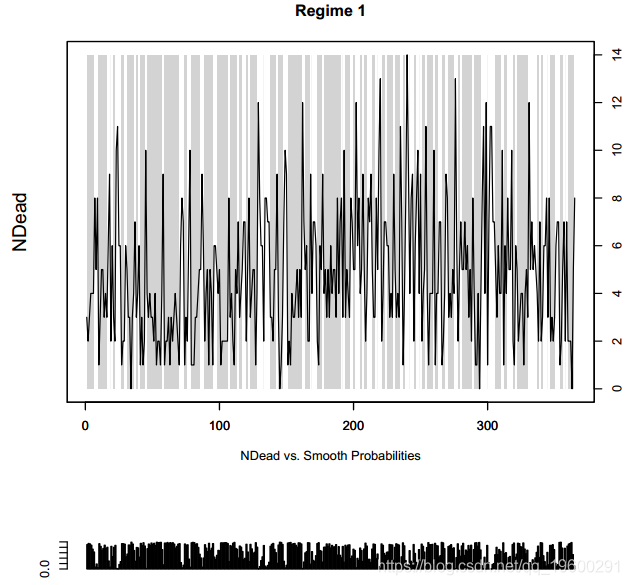
我们可以看到短时间内的状态分配,因为较大的状态基本上包含工作日。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证



