在本笔记本中,我们向读者介绍了基本的随机波动率模型,并通过连续序列重要性重采样讨论了它们的估计。我们使用收益率数据集来讨论 CSIR 在随机波动率模型估计中的实现和性能。
令 yt 为时间 t 的股票收益,σt 为其标准差。
第一个随机波动率模型
考虑以下离散时间随机波动率模型:
zt∼N(0,1) 和 ηt∼N(0,τ2) ,
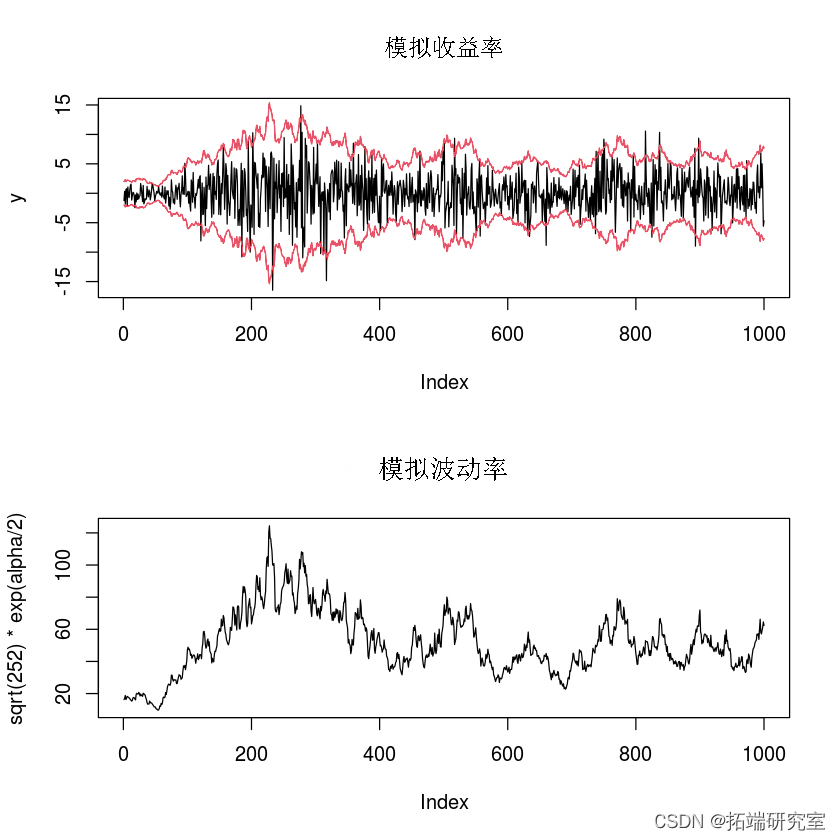
τ>0 和 |φ1|<1 以确保波动率遵循平稳过程。直观地说,波动过程被建模为一个潜在过程,其中 log(σ2t) 遵循 AR(1) 过程。在下一个块中,我们模拟了这个过程。在笔记本上,我们将继续处理这些模拟数据。为简洁起见,我们定义 αt=log(σ2t) 和 θ=(ϕ0,ϕ1,τ) 为参数向量。
## ##我们模拟数据。 ##我们设定pi_0 = 0.05, pi = 0.98, tau = 0.02 ##模拟数据的函数 #Input 2: T - 时间序列的大小 #Ouput: retF - 模拟的收益率(y)和波动率(alpha)。 pi <- thta\[2\] # 自相关系数 phi tu2 <- heta\[3\] # 具有tau2方差的正常误差
eta <- rorm(T, 0, sqrt(tau2)) # AR(1)波动率模型的误差
z <- rnrm(T, 0, 1) # 倍增项回报模型
alha\[1\] <- cost # 在开始阶段没有自相关的观察值
# 仿真时间序列
smdf <- s_sm(theta, T)
y <- smdf$y
lpa <- smdf$apha隐马尔可夫模型:定义
上面显示的模型属于更一般的隐马尔可夫模型类。设 h(αt|αt-1;θ) 为跃迁密度,g(yt|αt;θ) 为测量密度。那么在这种情况下,跃迁密度和测量密度都是高斯的,其中 和 .
序列蒙特卡罗
对于估计,我们使用序列蒙特卡罗,通过生成 P 随机抽取,称为“粒子”,以近似预测和过滤密度。虽然有很多变体,但我们只讨论(连续)序列重要性重采样(SIR)。
随时关注您喜欢的主题
SIR有两个步骤,预测和过滤步骤。
预测步骤 如下:
- 输入:粒子 从 ;
- 输出:对于每个粒子 利用跃迁密度对系统进行传播,得到一个新的预测粒子,即
具有连续序列重要性重采样的过滤步骤:算法
连续序列重要性重采样(CSIR) 是 SIR 的一种变体,它提供了过滤粒子的连续版本。
该方法的主要优点是它确保模拟似然相对于参数 θ 的向量是“平滑的”,以便能够使用基于梯度的优化方法进行优化。
使用 CSIR 的过滤步骤的算法如下:
- 输入:
- 具有条目 u(j) 的排序均匀随机采样向量(拒绝采样);
- 对于定义为 W(i)t 的每个粒子 α(i)t 在 yt 处评估的正态 PDF;
- 从预测密度 α(i)t 中排序。
代码
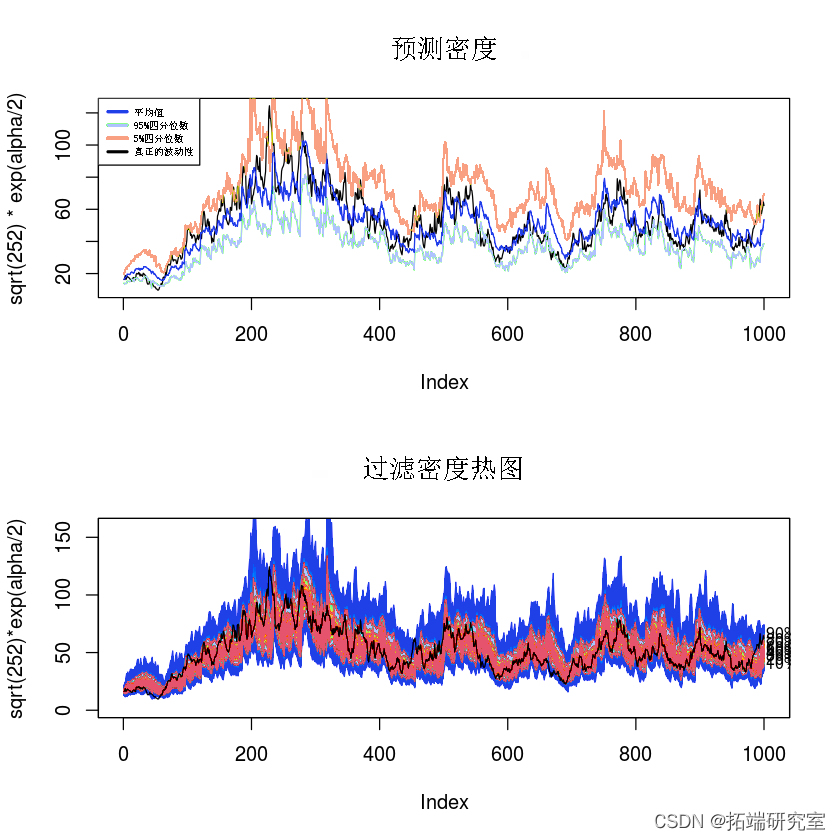
下面我们生成粒子集,并使用 SIR 近似过滤和预测密度。在第一个图中,我们显示了预测密度平均值及其 95 和 5 分位数。在同一个图中,我们还绘制了波动率的真实值。在第二个图中,我们绘制了过滤密度的热图。黑线是真正的波动率。
# --> (原始)序列重要性取样算法:过滤步骤
# 输入 1: appr - 预测密度
# 输入 2: aha_t - 在 y\[t\]评估的正态 pdf
# 输入 3: u - 排序均匀的随机采样向量(拒绝采样)
# 输出:alphp - 粒子过滤
# 排序和加权的速度减慢
alhawt <- alph\_wt/sum(alpha\_wt)
alpa\_rt <- cbind(seq(1,P,1),alpha\_pr)
alhapr\_id <- lpha\_sort\[order(alha_r\[,2\]),\]。
alhapr <- alpha_ridx\[,2\]
alph\_ix <- alha\_p_idx\[,1\]
alha\_wt <- alp\_w\[alpha_idx\]
alhacwt <- c(0, cumsum(alpha_wt))
j <- 1
for (i in 1:P)
while((aphawt\[i\] < u\[j\]) && (u\[j\] <= alpawt\[i+1\])){
lp\_up\[j\] <- alpa\_r\[i\] 。
}
# ----------------------------------------------------------------------
# 设置粒子过滤
# ----------------------------------------------------------------------
P <- 200 # 设置粒子的数量
lph_up <- rnorm(P,0,0.1)
alpar <- rep(0,P)
aha_w <- rep(1,P)/P
alphup_mt <- matrix(rep(0,T*3),T)
ala_pmat <- matrix(rep(0, T*3),T)
ah_prare <- matrix(rep(0, T*20),T)
# 从一个近似值中生成一个由P个随机抽样组成的粒子集
# 每个时间序列点的预测和过滤分布的近似值
for (t in 1:T){
# 预测步骤
appr <- nst + phi * alpp + rnorm(P,0,srt(tau2))
# 更新/过滤步骤(态密度)
ahat <- dnorm(y\[t\]*rep1,P), mean=0 , sd = exp(phar/2)
alpap <- sir(alhapr=aph\_r,alhawt=alpa\_t, u=sort(runif(P,0,1))
# 绘制预测密度图
plot(sqrt(252) * exp(alpha/2), type='l')
## 筛选密度热图
het <- matrix(rep(1,T*20), T, 20)
plot(NULL, xlim = c(1, T), ylim = c(0, 160), main="过滤密度热图",
在下一部分中,我们提供了 CSIR 的 R 和 C 版本。R 版本仅出于代码可读性的目的而提供。
###连续序列重要性重取样:过滤步骤
# 输入 1: alppr - 预测密度
# 输入 2: alhawt - 在 y\[t\]处评估的正态 pdf
# 输入 3: u - 排序均匀的随机采样向量(拒绝采样)
# 输出:ala_up - 粒子过滤(连续版本)。
# R版本(性能较慢)
cir <- function(aph_r, phwt, u) {
P <- length(aphpr)
al_p <- rep(0,P)
# 排序和加权的速度减慢
alpha\_wt <- alpha\_wt/sum(alpha_wt)
j <- 1
for (i in 1:P){
while((a_ct\[i\] < u\[j\]) & (u\[j\] <= alhwt\[i+1\])){
alh\_u\[j\] <- aph\_pr\[i\] + ((apapr\[i+1\]-alar\[i\])/(ala\_ct\[i+1\]-alpha\_cwt\[i\]) * (u\[j\]-ala_wt\[i\])
}
csir.c <- function(alppr, aht, u) {
P <- length(alpap)
ala_u <- rep(0,P)
.C("cir", alpup=as.dole(aphup),
alha\_pr=as.double(aha\_r),
alh_wt=as.doublephawt),
u=as.double(u),
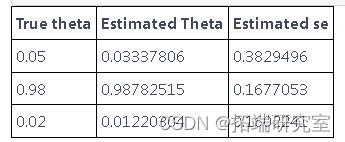
我们现在提供用于最大化对数似然和估计参数 θ 的代码。为了计算标准误差,我们使用在 MLE 评估的对数似然的 Hessian 矩阵的逆矩阵的对角线。
我们现在可以转到参数 θ 的估计。使用 C 中的函数进行估计。
vas <- sfit(y, c(0.5,0.5,0.5), P, 1)
## 显示结果 matrix <- cbind(heta_mle ,eta_se) 矩阵
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程
llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python、SPSS单指数、FF三因子模型、决策树分析沪深300指数、申万风格指数、10年期国债收益率、300ETF期权波动率指数数据优化金融期货市场预测|附代码数据
Python、SPSS单指数、FF三因子模型、决策树分析沪深300指数、申万风格指数、10年期国债收益率、300ETF期权波动率指数数据优化金融期货市场预测|附代码数据 Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别
Python可口可乐股票交易数据分析:KMeans-RF-LSTM多模型融合聚类、随机森林回归价格预测与交易模式识别



