线性回归时若数据不服从正态分布，会给线性回归的最小二乘估计系数的结果带来误差，所以需要对数据进行结构化转换。
在讨论回归模型中的变换时，我们通常会简单地使用Box-Cox变换，或局部回归和非参数估计。
这里的要点是，在标准线性回归模型中，我们有
可下载资源
视频
逆变换抽样将数据标准化和R语言结构化转换：BOX-COX、凸规则变换方法
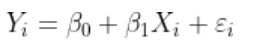
但是有时候，线性关系是不合适的。一种想法可以是转换我们要建模的变量，然后考虑
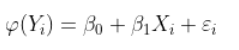
这就是我们通常使用Box-Cox变换进行的操作。另一个想法可以是转换解释变量，
我们测得一些数据，要对数据进行分析的时候，会发现数据有一些问题使得我们不能满足我们以前分析方法的一些要求（正态分布、平稳性）为了满足经典线性模型的正态性假设，常常需要使用指数变换或者对数转化，使其转换后的数据接近正态，比如数据是非单峰分布的，或者各种混合分布，我们就需要进行一些转化，这种转化类似于我们去网上买美国的食品，它上面写着这个食品是多少美元/磅，但是我们不清楚到底这是贵还是便宜，我们就需要把计量单位转化为元/kg，转化后我们就能明白到底是什么价位，box-cox也是这个意思。
box-cox变换的目标有两个：一个是变换后，可以一定程度上减小不可观测的误差和预测变量的相关性。主要操作是对因变量转换，使得变换后的因变量于回归自变量具有线性相依关系，误差也服从正态分布，误差各分量是等方差且相互独立。第二个是用这个变换来使得因变量获得一些性质，比如在时间序列分析中的平稳性，或者使得因变量分布为正态分布。
要明白什么是极大似然法，就需要理解似然函数。似然函数是一种关于统计模型参数的函数，一般表示为 ，它是给定测量到的样本分布x的情况下，关于参数
的函数。
其中 是指未知参数，它属于参数空间。x是样本分布。你可以把似然理解为概率，但是它又不完全等同概率。似然函数是参数取值的概率，在坐标系上，似然函数横左边是参数的取值，纵坐标也就是因变量是参数在已经测量的样本下取相应值的概率。
回到box-cox变换，极大似然法就是求出似然函数的值最大的时候，参数的取值为极大似然法。在box-cox变换中，需要对因变量进行转换，使得因变量的分布服从正态分布，box-cox的转换公式如下：
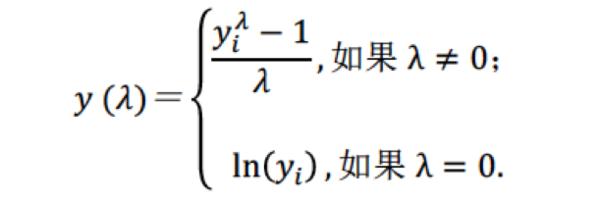
在这里可以看到 的值是需要我们自己去确定的，那么怎么去确定呢，这里使用的方法是假设经过转换后的因变量就是服从正态分布的，然后画出关于
的似然函数，似然函数值最大的时候
的取值就是这里需要确定的值。
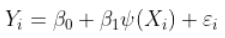
例如，我们有时会考虑连续的分段线性函数，也可以考虑多项式回归。
“凸规则”变换
“凸规则”(_Mosteller_. F and _Tukey_, J.W. (1978). Data _Analysis_ and _Regression_)的想法是，转换时考虑不同的幂函数。
1.“凸规则”为纠正非线性的可能变换提供了一个起点。
2 .通常情况下，我们应该尝试对解释变量进行变换，而不是对因变量Y进行变换，因为Y的变换会影响Y与所有X的关系，而不仅仅是与非线性关系的关系
3.然而，如果因变量是高度倾斜的，那么将其转换为以下变量是有意义的
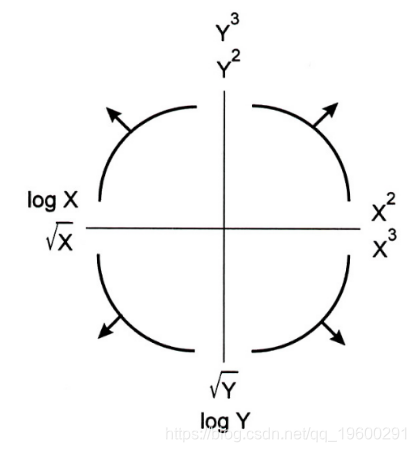
更具体地说，我们将考虑线性模型。
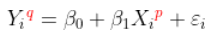
根据回归函数的形状（上图中的四个曲线，在四个象限中），将考虑不同的幂。
例如让我们生成不同的模型，看看关联散点图。
> plot(MT(p=.5,q=2),main="(p=1/2,q=2)")
> plot(MT(p=3,q=-5),main="(p=3,q=-5)")
> plot(MT(p=.5,q=-1),main="(p=1/2,q=-1)")
> plot(MT(p=3,q=5),main="(p=3,q=5)")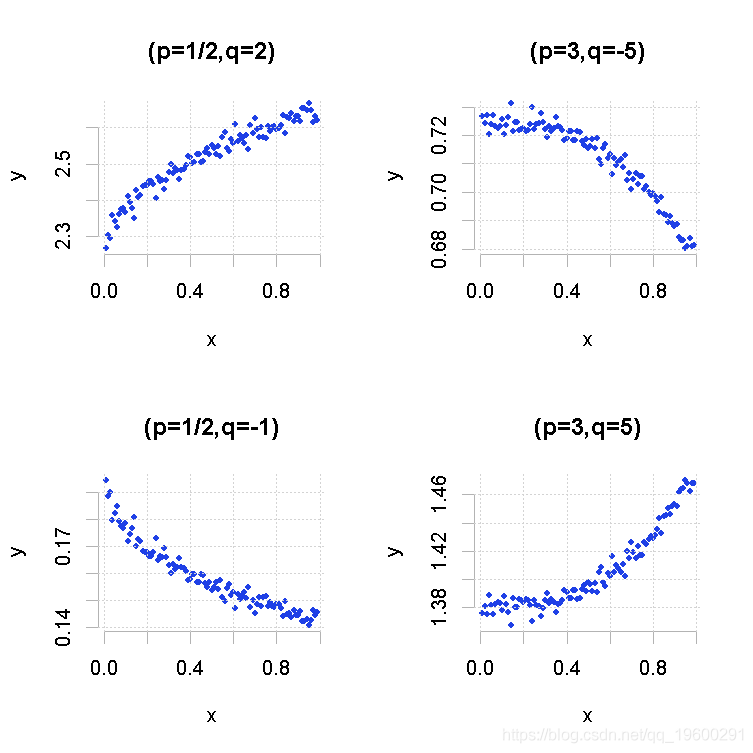
如果我们考虑图的左下角部分，要得到这样的模式，我们可以考虑
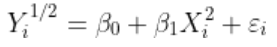
或更一般地
其中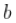
和都大于1.并且
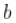越大，回归曲线越凸。
让我们可视化数据集上的双重转换，例如cars数据集。
> tukey=function(p=1,q=1){
+ regpq=lm(I(y^q)~I(x^p),data=base)
+ u=seq(min(min(base$x)-2,.1),max(base$x)+2,length=501)
+ polygon(c(u,rev(u)),c(vic\[,2\],rev(vic\[,3\]))^(1/q)
+ lines(u,vic\[,2\]^(1/q)
+ plot(base$x^p,base$y^q,xlab=paste("X^",p,sep=""),ylab=paste("Y^",q,sep="")
+ polygon(c(u,rev(u))^p,c(vic\[,2\],rev(vic\[,3\])),density=40,border=NA)
+ lines(u^p,vic\[,2\])
例如，如果我们运行
> tukey(2,1)我们得到如下图，
随时关注您喜欢的主题
左侧是原始数据集，右侧是经过转换的数据集，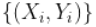
其中有两种可能的转换。在这里，我们只考虑了汽车速度的平方（这里只变换了一个分量）。
在该转换后的数据集上，我们运行标准线性回归。我们在这里添加一个置信度。然后，我们考虑预测的逆变换。这条线画在左边。问题在于它不应该被认为是我们的最佳预测，因为它显然存在偏差。请注意，在这里，有可能考虑另一种形状相同但完全不同的变换
> tukey(1,.5)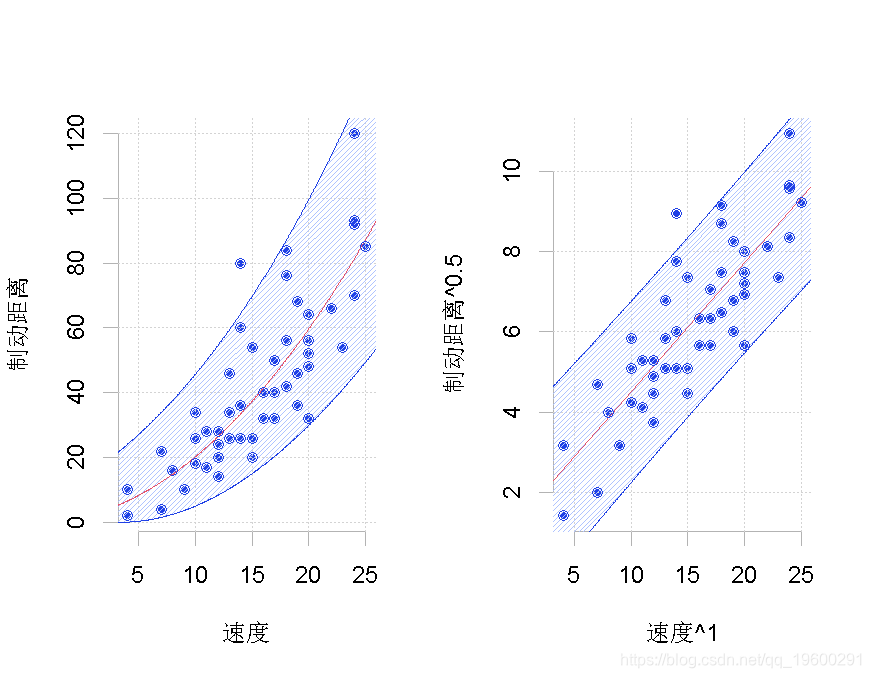
Box-Cox变换
当然，也可以使用Box-Cox变换。此外，还可以寻求最佳变换。考虑
> for(p in seq(.2,3,by=.1)) bc=cbind(bc,boxcox(y~I(x^p),lambda=seq(.1,3,by=.1))$y)
> contour(vp,vq,bc,levels=seq(-60,-40,by=1),col="white")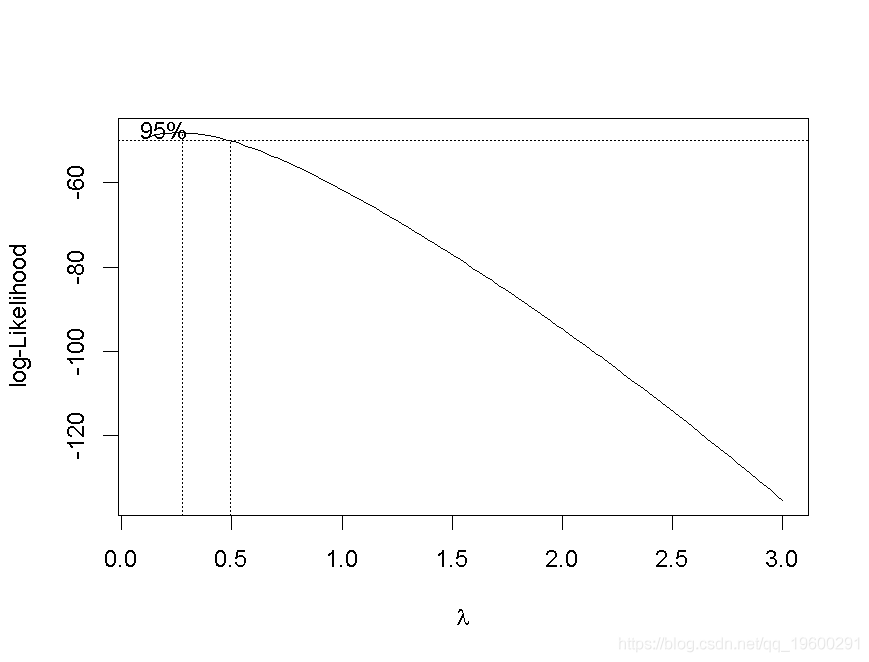
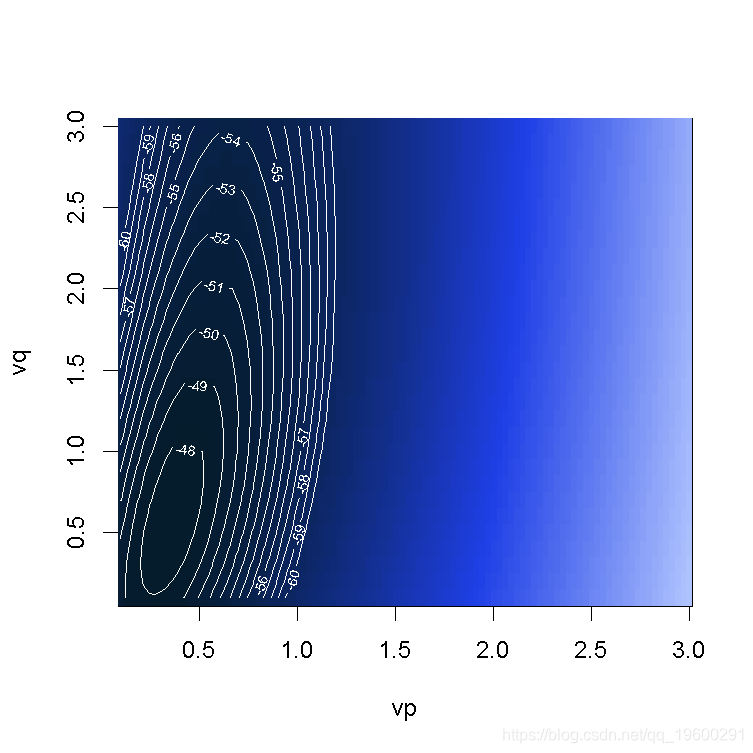
颜色越深越好（这里考虑的是对数似然）。 最佳对数在这里是
> bc=function(a){p=a\[1\];q=a\[2\]; (-boxcox(y~I(x^p),data=base,lambda=q)$y\[50\]
> optim(c(1,1), bc,method="L-BFGS-B")
实际上，我们得到的模型还不错，
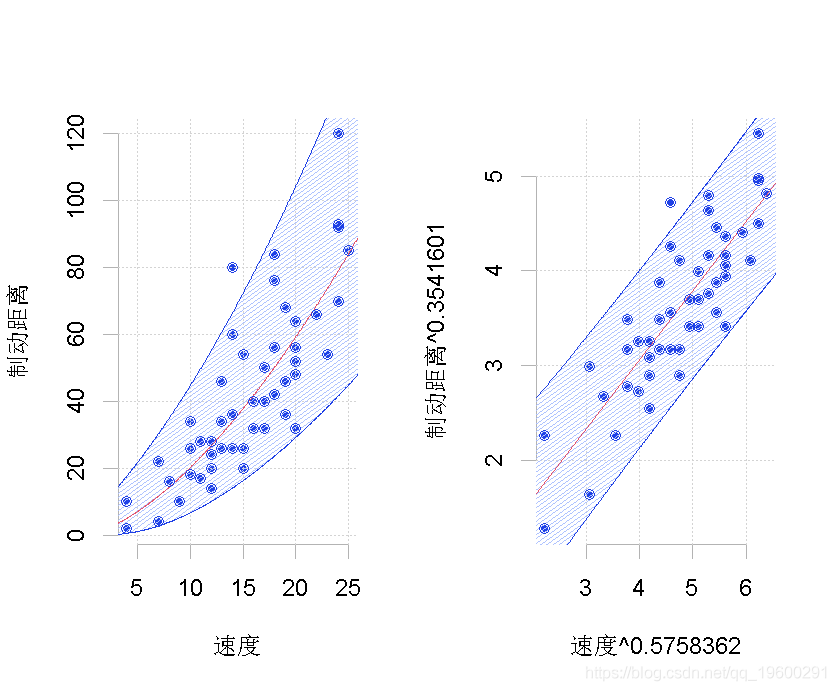
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
