近似贝叶斯计算和近似技术基于随机模拟模型中的样本计算近似似然值。
在过去几年中引起了很多关注，因为它们有望为任何随机过程提供通用统计技术。
一位同事向我询问我们在文章中讨论过的近似贝叶斯计算 MCMC (ABC-MCMC) 算法的简单示例。
可下载资源
下面，我提供了一个最小的示例，类似于Metropolis-Hastings 。
ABC：Approximate Bayesian computation
近似贝叶斯计算：指的是模拟不同参数下的数据，并将其与真实数据进行比较分析，直到与真实的数据最为接近，此时的参数就为最优值。贝叶斯统计公式：P(D/θ)=P(θ/D)*P(θ)/P(D) ，贝叶斯统计可以简单的理解为结果已知求不同原因下概率，从而解释导致如今结果最可能的原因；这需要计算似然函数P(θ/D)（为了防止先验概率为0，求解似然函数过程中引入拉普拉斯修正（例如取自然对数））、先验分布P(θ)以计算后验分布P(D/θ)；简单模型下的似然函数容易求解，但对于复杂的模型, 似然函数难以求出, 只能尝试用模拟产生出资料的方式, 反过来设法逼近似然函数的效果；ABC中的A指的就是对似然函数的趋近；
具体举例：如下假设已有一个似然函数未知且有参数t的模型M(t), 及观测到的资料集D_observed，从t的先验分布中抽出n个t参数, 并分别产生n个模型 {M(t_k) : k from 1 to n}, 由模型产生模拟(simulate)的资料, 记作 {D(t_k): k from 1 to n}接下来对对各个k, 比较模拟产生的资料集D(t_k)跟实际观测到的资料observed, 若是两者统计性质差太多的话, 则拒绝掉t_k, 反之则接受t_k，把所有被接受的参数t_k集合起来, 作为参数t的后验分布。
MCMC：Markov Chain Monte Carlo
马尔可夫链蒙特卡洛方法：在贝叶斯理论框架下，通过计算机进行模拟的蒙特卡洛方法，该方法将马尔可夫过程融入到了蒙特卡洛模拟中，实现了抽样分布随着模拟的进行而改变的动态模拟，弥补了传统蒙特卡洛积分只能静态模拟的缺陷。
在统计学中，马尔可夫链蒙特卡罗（MCMC）算法旨在从给定的概率分布中生成样本。该方法名称中的“蒙特卡罗”部分是出于取样目的，而“马尔可夫链”部分来自获取这些样本的方式。为了得到样本，要建立一个马尔可夫链，从其平稳分布中获得样本。然后，可以从马尔可夫链中模拟随机的状态序列，该序列足够长，能够（几乎）达到稳态，再保留生成的一些状态作为样本。
在随机变量生成技术中，MCMC是一种相当高级的方法，可以从一个非常困难的概率分布中获得样本，这个概率分布可能仅由一个乘法常数定义。更出乎意料的是，可以用MCMC从一个未经标准化的分布中获得样本，这来自于定义马尔可夫链的特定方式，马尔可夫链对这些归一化因子并不敏感。
library(coda)
假设数据是正态分布的10个样本
平均值为5.3，SD为2.7
data = rnorm
# 我们想用ABC来推断出所使用的参数。
# 我们从同一个模型中取样，用平均值和方差作为汇总统计。
# 当我们接受ABC时，我们返回真，因为与数据的差异小于某个阈值ABC <- function(pr){
# 先验避免负的标准偏差
if (par <= 0) return(F)
# 随机模型为给定的参数生成一个样本。
samples <- rnorm
# 与观察到的汇总统计数字的比较
if((difmean < 0.1) & (difsd < 0.2)) return(T) else return(F)
}
我们将其插入一个标准的metropolis Hastings MCMC中。
用metropolis 的接受度来交换ABC的接受度
MCMCABC <- function(saue, itns){
for (i in 1:ieraos){
# 提议函数
prp = rnorm(2,mean = chain\[i,\], sd= c(0.7,0.7))
if(A_ance(prl)){
chn\[i+1,\] = prl
}else{
chn\[i+1,\] = cain\[i,\]
}
}
return(mcmc(cin))
}plot(psor)
结果应该是这样的：
随时关注您喜欢的主题
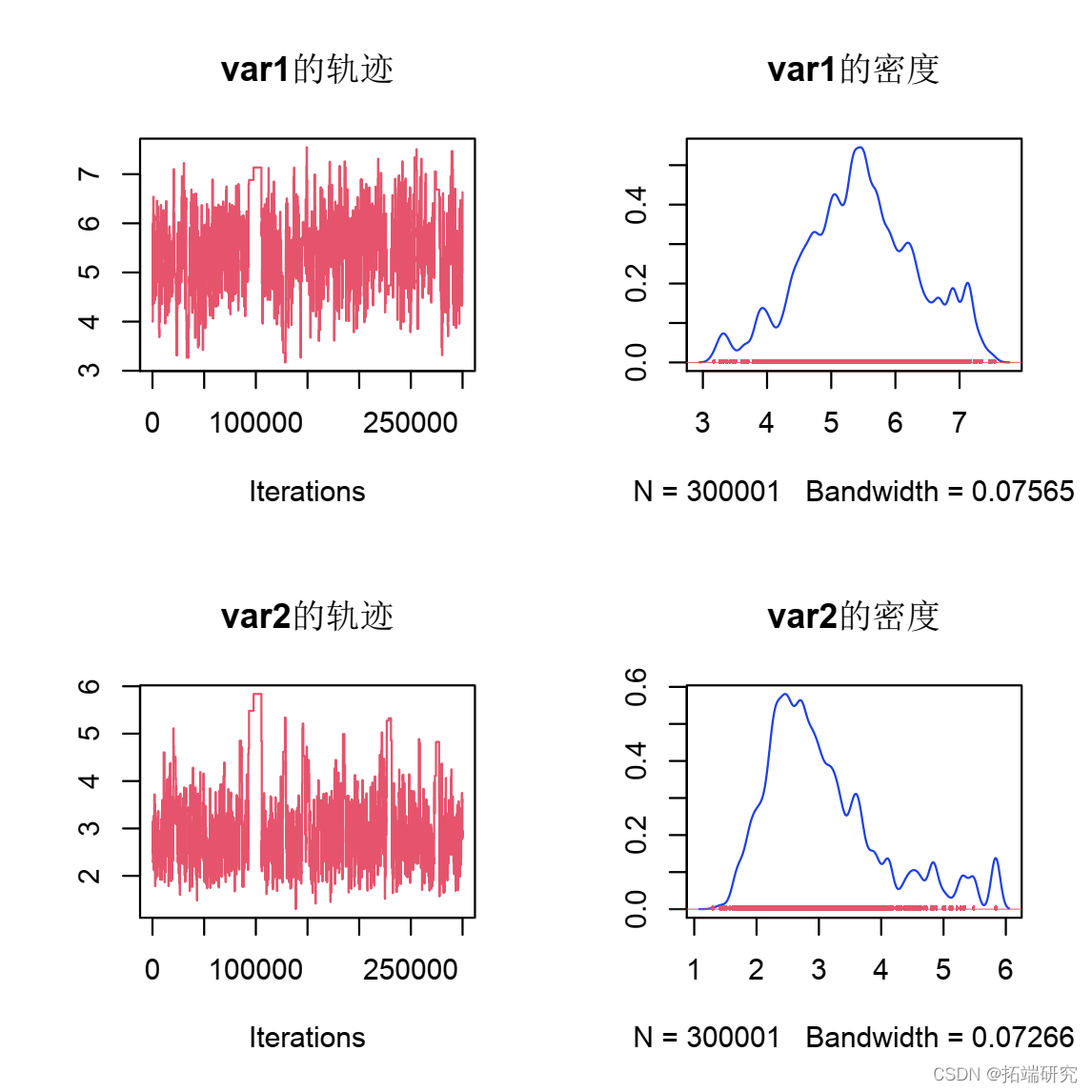
_图_：后验样本的轨迹图和边缘图。从右边的边缘图中，您可以看到我们正在近似检索原始参数值，即 5.3 和 2.7。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
MATLAB贝叶斯优化混合Bayes-CNN-RNN分析股票市场数据与浅层网络超参数优化
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
