在网络上进行社区检测时，有时我们不仅拥有实体之间的联系。
这些实体代表了我们可能也想在网络可视化中代表的现实事物。
plot(g)
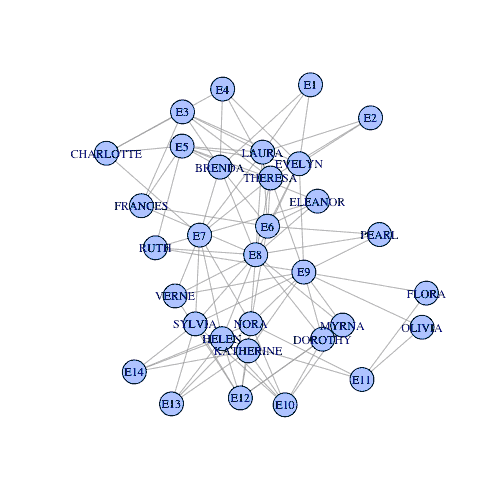
网络中的社群的基础定义：紧密连接的节点集合，这些节点间有较多的内部连接，而相对较少的外部连接；
Zachary空手道俱乐部一个在图这块入门级的数据集，用来展示图网络中基本的问题如节点分类、社区发现等等；
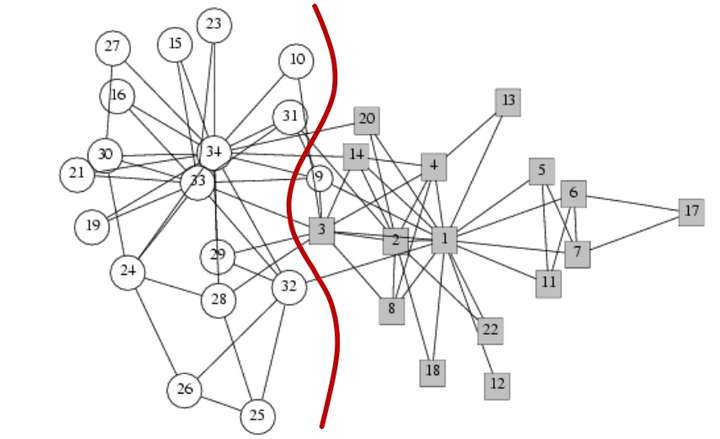
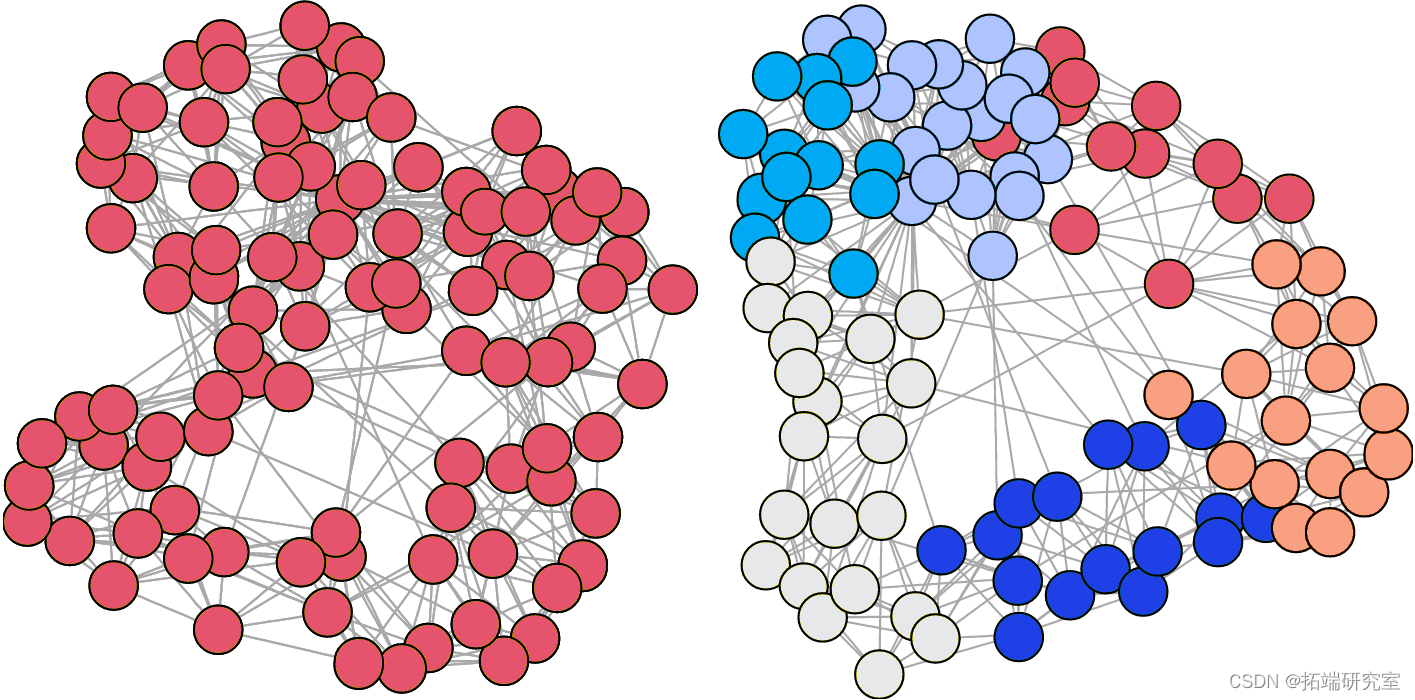
如下图， 仅靠图的结构化关系，可以比较合理地将俱乐部进行切分，即规划至各自的社群：
另一个例子是NCAA FootBall Network：
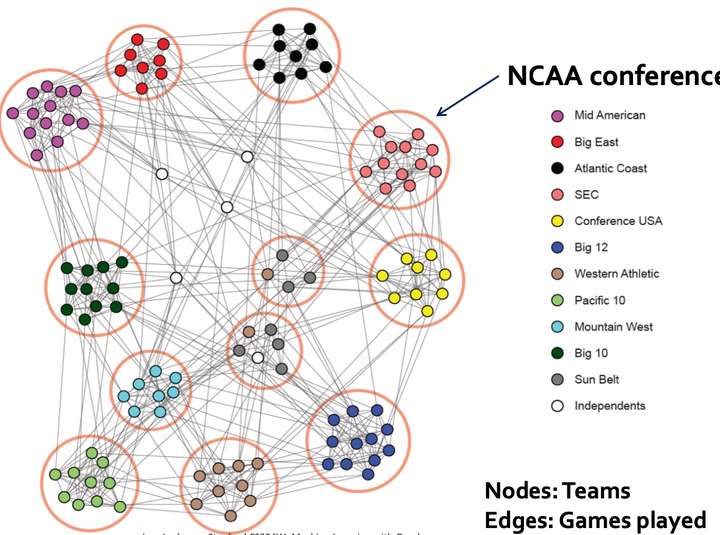
如何寻找网络中的社群？
Modularity Q用来衡量网络中社群划分的指标， 其基础含义如下：
其中 需要构建null model（之前的学习笔记有提到过Configuration Model， 忘记了的小伙伴可以翻一下）， 保证相同的degree distribution且连接概率为均匀随机， 假定两个节点i、j，其度分别为
，那么节点间边的期望为
，所以这个图里面所有边的期望为：
所以Modularity Q从：
表示为：
其
Q值域为[-1, 1], 正值表示社群内的边多于期望， 当Q为0.3-0.7之间表明有显著的社群结构；
我使用数据集，代表了观察到的 18 位女性参加 14 场社交活动的情况。
不考虑这个图是二向图，让我们尝试将图划分为社区。有自然的分界线吗？让我们根据节点所属的社区为节点着色：
community(g) col <- membership + 1 plot
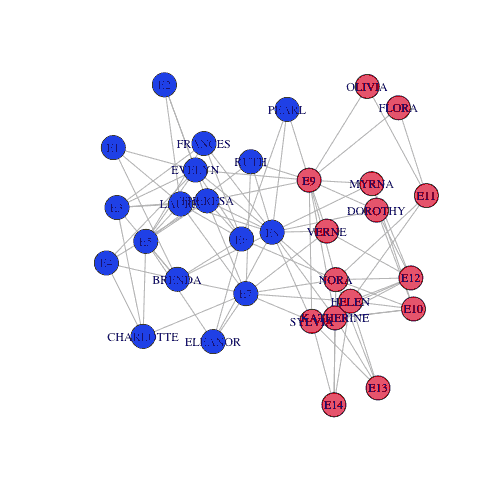
正如我们所看到的，该算法找到了2个社区，乍一看，这种划分似乎是合理的。无论如何，还有一种自然的划分是算法无法找到的：事件/女性的二元关系。每个节点都有这样的属性：”是女性 “或 “是事件”。让我们用不同的方式来描述这个图的特征。我们有14个事件。对于这些，我们改变它们的形状。
shape <- "squa" shape <- "cice" plot(g)
如何从给定的网络中提取社区？
在网络中寻找社区是复杂系统范式下的一项常见任务。有几种方法可以使用非常不同的包对图进行社区分区。
网络社区检测算法
walktrap.community
该算法通过执行随机游走找到密集连接的子图。这个想法是随机游走将倾向于留在社区内，而不是跳到其他社区。
随时关注您喜欢的主题
边缘.中间.社区
这个算法就是Girvan-Newman算法。它是一种分割算法，在每一步中，具有最高间性的边被从图中移除。对于每一次划分，你都可以计算出图的模块化程度。最后，在这个过程给你带来最高模块化值的地方选择切割树状图。
Newman快速算法(fast greedy)
该算法是纽曼算法。在这种情况下，算法是凝聚的。在每一步，两组合并。合并是通过优化模块化决定的。这是一种快速算法，但有一个贪婪算法的缺点。因此，虽然我发现它有用且准确，但它可能不会产生最佳的整体社区划分。
自旋玻璃社群发现
该算法使用自旋玻璃模型和模拟退火来查找网络内的社区。
# 首先我们加载ipgrah软件包 # 让我们生成两个网络并将其合并为一个图。 graph.union # 让我们删除多线和循环 simplify # 让我们用Grivan-Newman算法看看这里是否有社区。 # Grivan-Newman算法 # 首先，我们计算边缘间性、合并等。 edge.betweenness.community # 现在我们有了合并/拆分，我们需要计算模块化。 # 对于每个合并，我们将使用一个函数，对于每个边被删除，将创建第二个图，检查其成员资格并使用该成员资格来计算模块化程度 membership # -在原图g上计算模块化 modularit # 我们现在可以绘制所有模块化的图 plot # 现在，让我们根据节点的成员资格为其着色 removed.edges color=membership # 让我们为图选择一个布局 layout # 绘制 plot # 使用 fastgreedy.community agorithm plot
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python复杂网络社区检测：并行谱聚类算法设计与多种算法应用实战研究
R语言对git安卓包分类统计、聚类、复杂网络可视化分析
报告分享|网络直播文艺生态报告
R语言社区发现算法检测心理学复杂网络：spinglass、探索性图分析walktrap算法与可视化
