
网络流也可以解决很多问题,比如如何进行道路交通管控,以便有效地缓解早高峰的拥堵;在物流网运输中,在满足供需关系的同时,怎样使渠道成本最低;在轰炸机执行轰炸任务时,怎样才能给敌军补给线造成更严重的打击。这些问题都有现成的网络流算法,别再以为网络流仅仅是网络中的比特流。
对于网络和网络流的实践,我们将使用R。
网络的定义
一个网络N=(V,A)是指一个连通无环弧且满足下列条件的有向图:
①有一个顶点子集X,其每个顶点的入度都为0;
②有一个与X不想交的子集Y,其每个顶点的出度都为0;
③每条弧都有一个非负的权值,称之为弧的容量。
以上定义中X称之为源点集,Y称之为汇点集,其他的顶点称之为中转点,网络的容量函数为C。
上图所示的两个网络中,(a)中的x1,x2为源点,y1,y2为汇点,其他的节点则为中转点。
如果一个网络中只有一个源点和汇点,则称之为单源单汇网络,当然任何一个网络都可以导出一个单源单汇网络,方法如下:
(1)给网络N添加两个顶点s和t;
(2)对∀x∈X,从s向x连接一条弧,其容量为∞,或者x的邻接边的容量和;
(3)对∀y∈Y,从y向t连接一条弧,其容量为∞,或者y的邻接边的容量和;
网络的流与割
流定义
定义:网络N=(V,X,Y,A,C)中的一个可行流的定义是定义在弧集A上的一个整值函数(网络就一般只讨论弧容量为整值的网络,弧值为小数的网络可类比于整值网络)f,使得:
(1)容量约束:流经管道的流量值应当不超过管道的容量——对∀a∈A,0≤f(a)≤c(a);
(2)流量守恒:对于每个结点,流入流出的流量应当守恒。
注意:可行流总是存在的,因为总是存在0值流。
流量最大的可行流称为最大流。
割定义
割定义:设N== (V,x,y,A,C)是一个单源单汇网络 。S⊆V, S’=V-S. 用(S,S’)表示尾在S中而头在S’中的所有弧的集合(即从S中的点指向S’之外点的所有弧之集)。若x∈S, 而y∈S’, 则称弧集((S,S’)为网络N的一个割。一个割(S,S’)的 容量是指(S,S’)中各条弧的容量之和,记为Cap(S,S’)。
如下图:
令S={x,v1,v2,v3,v5},则(S,S’)={v1v4,v3v4,v5v4,v5v6}(可以看出割只计算弧尾在源点一侧,而弧头在汇点一侧的边权值),所以割容量为Cap(S,S’)=9。
最小割定义
最小割定义:网络N中容量最小的割,也即假设K是网络N的一个最小割,则不存在割K’,使得CapK’<CapK。
对于网路中的任意割和任意流,流经割的流量守恒。
myflows <- flows(mat = nav, i = "i", j = "j",
diag(myflows) <- 0
选择流量至少要占每个市区流出流量总和的20%。
flows(myflows/rowSums(myflows)*100然后选择 主要流量 (流入流量标准)
flowSel2 <- domflows(mat = myflows, w = colSums(m
flowSel <- myflows * flowSel1 * flowSel2
data.frame(id = colnames(myflows), 最后绘制主导流图
opar <- par(mar = c(0,0,2,0))
pltFlows(mat = flowSel, spdfid = "ID", w = inflows, wid = "id",wvar = "w", wcex = 0.05, add = TRUE,legend.flows.pos = "topright",legend.flows.title =
title("通勤者的主要流动")获取背景图的代码基于该包中定义的 GE对象。
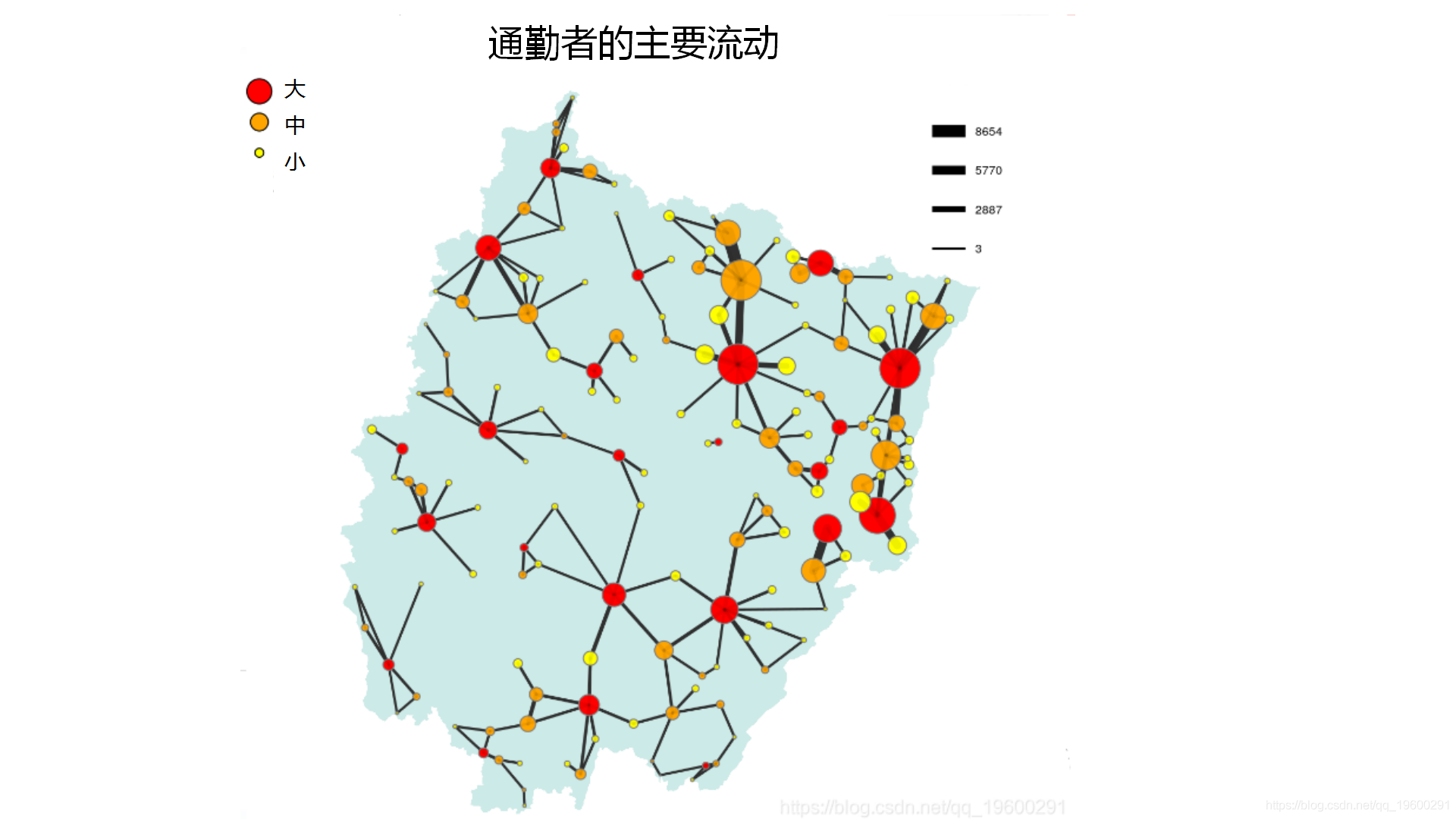
要进一步了解主流流量,请阅读 Nystuen&Dacey(1961)

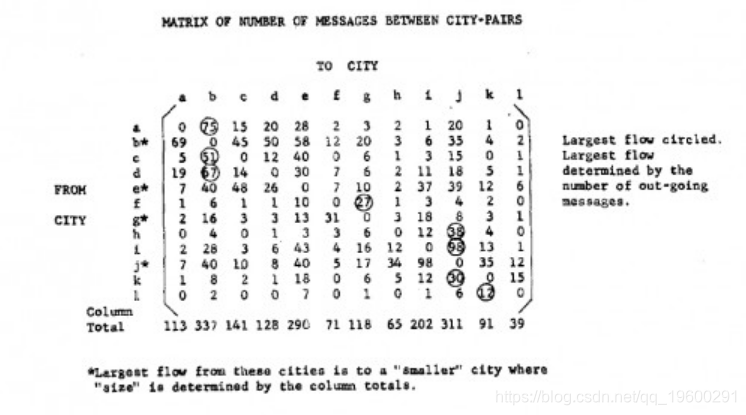
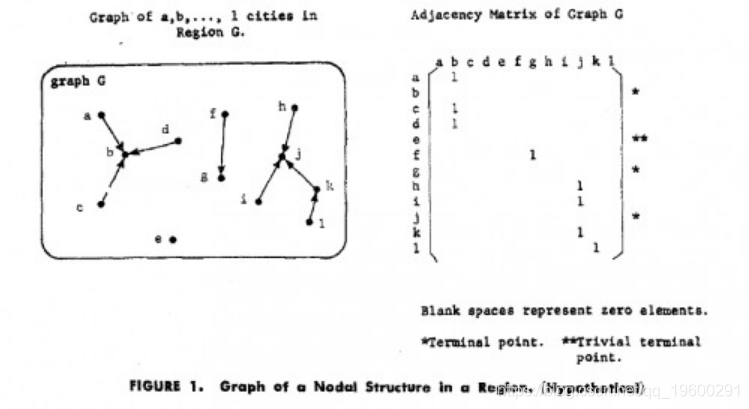
 2025有色金属行业前瞻报告:信用、ESG、新材料、全球化布局 | 附500+份报告PDF、数据、可视化模板汇总下载
2025有色金属行业前瞻报告:信用、ESG、新材料、全球化布局 | 附500+份报告PDF、数据、可视化模板汇总下载 LangGraphSwarm的银行数据分析群体智能代理:Text-to-SQL、EDA可视化与动态任务编排|附代码数据
LangGraphSwarm的银行数据分析群体智能代理:Text-to-SQL、EDA可视化与动态任务编排|附代码数据 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据



