我们在心理学网络论文中看到的一个问题是，作者有时会对其数据的可视化进行过度解释。
这尤其涉及到图形的布局和节点的位置，例如：网络中的节点是否聚集在某些社区。
下面我将详细讨论这个问题，并提供一个关于如何识别网络中项目社群的基本R教程。非常欢迎在下面的评论部分提出反馈。
这8个算法方便入门者熟悉社区发现算法。此处参考另外1篇对比这8个算法的文章：
Yang Z, Algesheimer R, Tessone C J. A comparative analysis of community detection algorithms on artificial networks[J]. Scientific Reports, 2016, 6(1): 1-18.
这8个算法分别是：
1.Edge-betweenness
这是Newman and Girvan (2004)提出的一种用于社区发现的算法，发表于PNAS。这两位作者在社区发现领域发表了许多文章，引用量极高，做出了很大的贡献。Edge-betweenness算法的核心想法是对于网络中的每一条边计算一个edge-betweenness centrality指标，然后按照edge-betweenness centrality从大到小不断删掉这些边，每次删掉一条边都要重新计算这个指标。这样一来就能形成一种类似层次聚类的效果，产生一个自上而下的树，实现社区发现。
Edge-betweenness算法的思想非常直观，效果也很好，只不过在计算速度上差强人意，其计算复杂度是O(m^2 n)，其中m是网络中边的数量，n是网络中节点的个数。
图片来源：Girvan and Newman (2002)
2.Fastgreedy
这是Clauset et al. (2004)提出的一种基于模块度的社区发现算法。该算法与Newman (2004)所采用的贪婪优化算法相同，因此给出的结果也相同。（注：部分网友将Newman (2004)提出的方法称为fastgreedy算法，在此我们以igraph包中cluster_fast_greedy函数所实现的Clauset et al. (2004)方法为准。）Newman (2004)提出的贪婪优化算法首先将网络中的每个节点都作为一个单独社区，然后选出使得模块度增值最大的社区对进行合并。如果网络中的所有节点属于同一个社区，则停止合并过程。最终我们得到一个自下而上的树，树的每一层切分对应着网络的某个具体划分。该算法的计算复杂度是O((m+n)n)。Clauset et al. (2004)利用稀疏邻接矩阵的数据结构，进一步提高了Newman (2004)算法的速度，算法复杂度降低为O(mdlogn)，其中d是树的深度。该算法可以分析有数百万个节点和数千万条边的大型网络。
3.Leading eigenvector
这是Newman (2006)提出的一种自上而下的分层社区发现算法。该算法的核心是定义了一个模块度矩阵（modularity matrix）。最大化模块度的过程可以体现在模块度矩阵的特征值分解中，模块度矩阵在社区发现中的作用类似于由图拉普拉斯算子在图划分中发挥的作用。首先计算模块度矩阵的最大正特征值所对应的特征向量，然后根据特征向量中元素的正负符号将节点分成两个社区。如果特征向量中的所有元素都具有相同的符号，则说明该网络没有底层的社区结构。该算法的复杂度为O((m+n)n)。
4.Infomap
该算法是Rosvall and Bergstrom (2008)和Rosvall et al. (2009)提出的基于信息理论原理的社区发现算法。该方法通过最优地压缩网络上信息流的描述，将网络分解为多个模块。
5.Label propagation
这是Raghavan et al. (2007)提出的一种快速、近线性时间的社区发现算法。该算法首先给每个节点指定唯一的标签，然后每个节点以同步方式获取其邻居的最频繁标签并将标签重新分配给节点。迭代更新节点标签，当每个节点的标签是其附近最频繁的标签之一时，该方法停止。
6.Multilevel
这是Blondel et al. (2008)提出的一种基于模块度度量的分层社区发现算法。最初，每个节点都单独作为一个社区。在每一步中，节点都以局部的、贪婪的方式重新分配给社区：每个节点都移动到对模块度提升最大的社区中。当没有节点可以重新分配时，每个社区被认为是一个单独的节点，重复上述过程。当只剩下一个节点，或者模块度不能在一个步骤中再增加时，该算法停止。
7.Walktrap
这是Pons and Latapy (2005)提出的一种基于随机游动的社区发现方法。该算法的主要思想是在网络中进行随机游走，游走更有可能停留在同一社区内，因为只有少数几条边通向社区之外。
8.Spinglass
这是Reichardt and Bornholdt (2006)和Traag and Bruggeman (2009)提出的一种社区发现方法。该算法扩展了现有的Potts模型，以检测同时存在正向和负向链接的复杂网络中的社区。该方法解决了社会平衡理论中长期存在的一个问题，即带符号网络的聚类问题。
节点部署和 Fruchterman-Reingold 算法
我们创建一个例子。首先，我们拿一些数据，估计一个正则化的偏相关网络，其中节点之间的边类似于偏相关，并使用’spring’命令绘制网络。这是心理学网络文献中默认的，使用Fruchterman-Reingold算法为图中的节点创建一个布局：具有最多连接/最高连接数的节点被放在图的中心。
cort<- cor(data) graph(cort,layout="spring")
matrix 是这 20 个项目的相关矩阵， Size 命令告诉我们有多少人。
这是结果图：
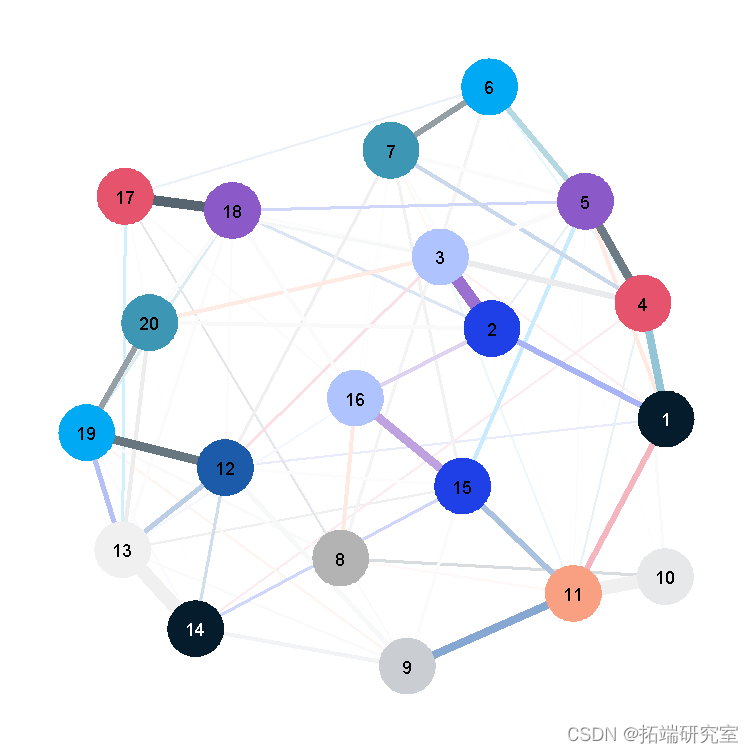
然而，这里的节点部署只是许多同样 “正确 “的节点部署方式中的一种。当网络中只有1-3个节点时，算法将总是以同样的方式部署它们（其中节点之间的边的长度代表它们之间的关系有多强），算法唯一的自由度是图形的旋转。但是，特别是在有许多节点的图中，部署方式只告诉我们一个非常粗略的结果，不应该被过度解释。
以下是绘制我们上述网络的另外两种方法，它们同样 “正确”。
nNd <- 20 set.seed(1) grh2<-grph set.seed(2) gr3<-grph
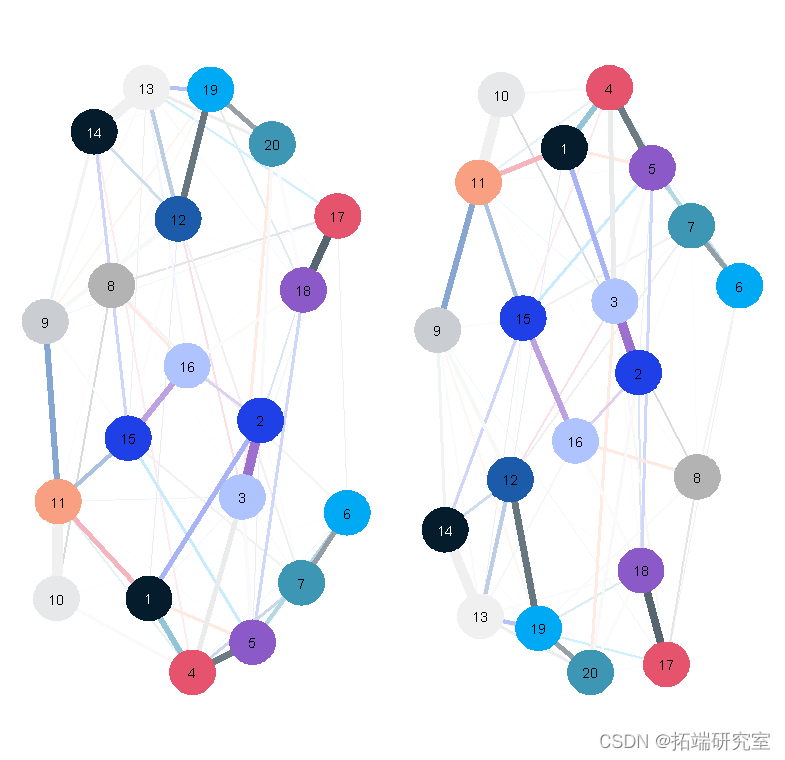
虽然项目之间的边显然是相同的，但节点的位置却有很大的不同。
欧洲神经精神药理学例子
《欧洲神经精神药理学》（European Neuropsychopharmacology）上Madhoo & Levine的一篇新论文为这个问题提供了一个很好的例子。他们在两个时间点（相隔12周）调查了约2500名被诊断为重度抑郁症的精神科门诊病人的14种抑郁症状的网络结构。这篇论文的一个非常不错的贡献是，他们研究了网络结构随时间的变化，其方式与我们以前在同一数据集中的研究有些不同。
与上面的网络例子类似，他们使用正则化的偏相关网络来估计两个时间点的横截面网络模型，并使用Fruchterman-Reingold算法绘制网络。他们通过目测得出结论，有4个症状群存在，而且这些症状群没有随时间变化。
“在基线时，网络由四个症状群组成（图1a），即：。睡眠障碍（项目1-5），认知和物理动机缺损（项目6-9），情感（项目10-12）和食欲（项目（13-14）。
[…]终点症状分组（图1b）与基线时相似”。
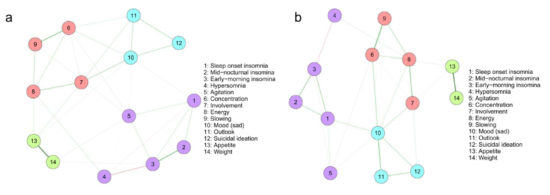
但这些发现和结论仅仅是基于对结果图的视觉检查–而我们在上面已经了解到，对这些图的解释应该非常谨慎。值得注意的是，这种视觉上的过度解读在心理学网络文献中相当常见。
让人眼前一亮的另一个原因是，我们在最近的一篇论文中分析了同一数据集的社群结构，发现社群的数量随时间而变化–这与作者对图表的视觉解释相冲突。
随时关注您喜欢的主题
R中的数据驱动的社群聚类
那么，如何在R中做到这一点？有许多可能性，我介绍三种：一种来自潜变量建模领域的非常成熟的方法（特征值分解）；一种来自网络科学的成熟算法（spinglass算法）；以及一种正在开发中的非常新的工具（使用walktrap算法的探索性图分析）。
特征值分解
传统上，我们想用潜变量框架来描述上述20个项目，问题是：我们需要多少个潜变量来解释这20个项目之间的协方差？一个非常简单的方法是查看数据中各成分的特征值。
plot(eigen) abline(h=1)
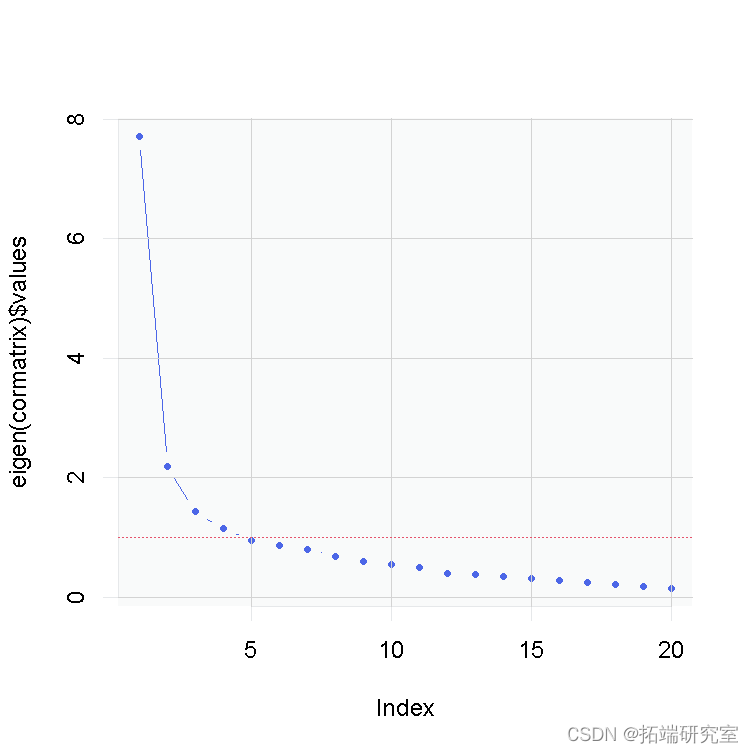
这向我们显示了Y轴上每个成分的每个特征值；X轴显示了不同的成分。一个高的特征值意味着它能解释项目之间的大量协方差。红线描述了所谓的标准：一个简单的规则，决定我们需要多少个成分来充分描述项目之间的协方差（每个成分的特征值>1）。无论如何，根据我们现在使用的规则，我们可能会决定提取2-5个成分。我们还不知道哪个项目属于哪个成分–为此，我们需要运行，例如，探索性因子分析（EFA），看看因子载荷。
为什么这与网络有关呢？
许多论文现在已经表明，潜变量模型和网络模型在数学上是等价的，这意味着在大多数情况下，支撑数据的因素的数量将转化为你在网络中可以找到的社区的数量。
Spinglass算法
第二种方法是所谓的spinglass算法，该算法在网络科学中已经非常成熟。为此，我们将上面估计的网络输入到R中。最相关的部分是最后一行membership。
spinglascmy(g) mershp
在我们的例子中，spinglass算法检测到了5个社区，这个向量代表了这20个节点属于哪个社区（例如，节点1-7属于社区5）。然后，我们可以很容易地在qgraph中绘制这些社区，例如，对节点进行相应的着色。请注意，iqgraph是一个非常通用的软件包，除了spinglass算法之外，它还有许多其他检测社区的可能性，比如walktrap算法。(感谢Alex Millner对igraph的投入；当然，这里所有的错误都是我的错误）。
值得注意的是，spinglass算法每次运行都会导致不同的结果。
这意味着你应该在运行spinglass.community之前通过set.seed()设置一个种子，而不是像我上面那样。我运行该算法1000次，看看得到的聚类数量的中位数，然后找到一个能重现这个聚类数量中位数的种子。我在一篇论文中使用了这个解决方案（注意，使用不同的种子，解决方案看起来是不同的）。
同样关键的是，要知道有许多种不同的方法来做社群检测。Spinglass有些简单化，因为它只允许项目成为一个社区的一部分–但可能项目被描述为同时属于几个社区更好。Barabási的书 “网络科学 “中有一个关于社区检测的广泛章节。Spinglass只是众多机会中的一个。正如我上面提到的：例如walktrap，也是常用的，而且更稳定。
探索性图分析
第三种方法是通过探索性图表分析。从你的数据中重新估计了一个正则化的部分相关网络，与我们上面所做的类似，然后使用walktrap算法来寻找网络中的项目社群。在使用walktrap算法的情况下，这应该会得到与igraph相同的结果（并且细节设置相同，比如步骤数）。
优点是–与特征值分解不同–它直接显示哪些项目属于哪些社群。
walktrap(da, plt= TRUE)
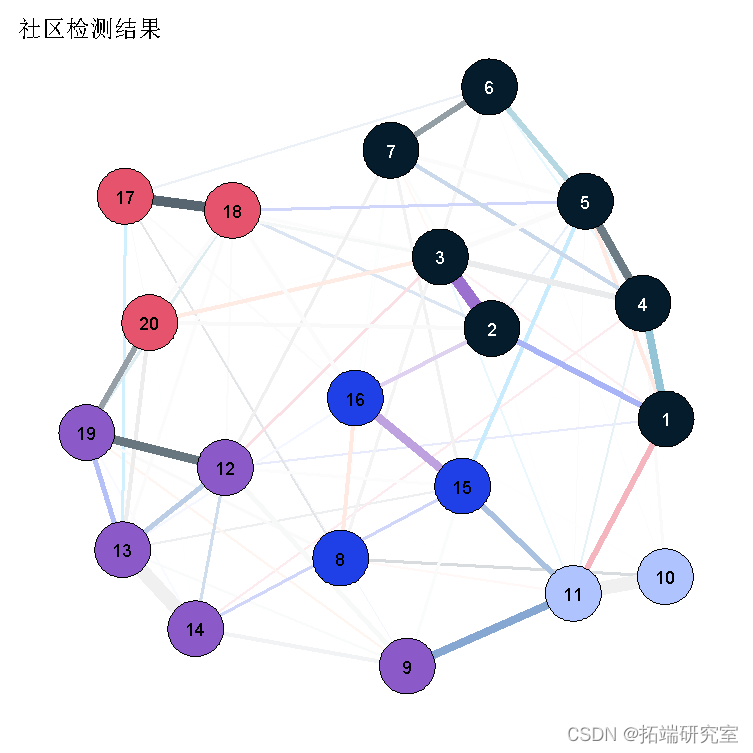
如果这个方法被证明是有效的，它非常容易使用，并自动显示你的项目属于哪个社区。
请注意，目前，探索性图分析采取你的数据并自动估计一个高斯图形模型（假设是多变量的正常变量）。
spinglass算法和walktrap算法结果是一样的吗？
现在，我们想检查一下我们的结果的稳健性：spinglass算法和使用walktrap算法在社区检测方面是否一致？
这很容易做到：让我们把这两个网络画在一起，并对社区进行相应的着色。首先，我们根据结果来定义社群，然后用上面第一个网络的布局来绘制网络。
walktrap(coate tile="walktap") spinglass(coratix, tite="spinglass")
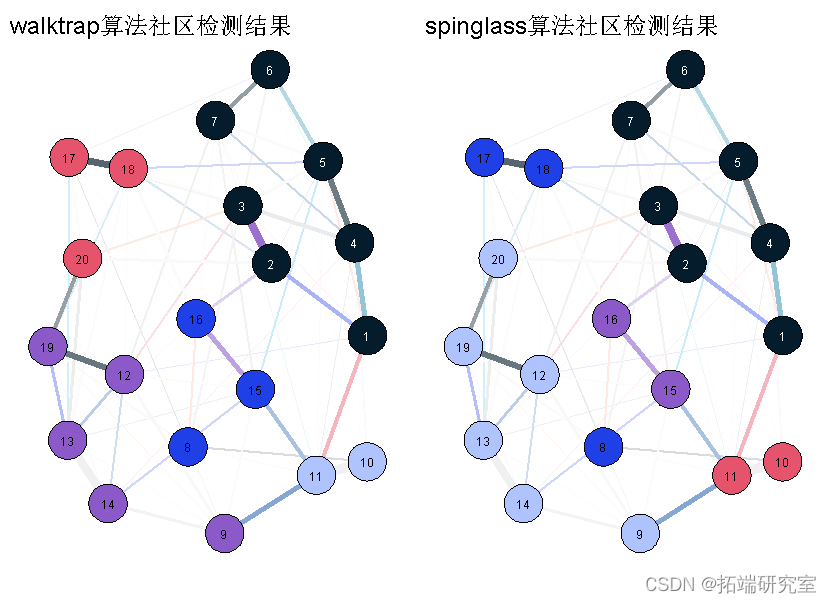
直觉上–基于视觉检查–walktrap的解决方案似乎更有意义，其中节点8属于蓝色社区而不是紫色社区。但是，同样，这只是复杂关系的图形显示，我们在这里必须谨慎解释。
因此，让我们用一个稍微不同的布局来绘制同一个网络。
walktrap(layou = list(int = atinomNe2,no,2))) spinglass(cori, layo.pr = list(iit=matrxnrm(Nd2)nde2
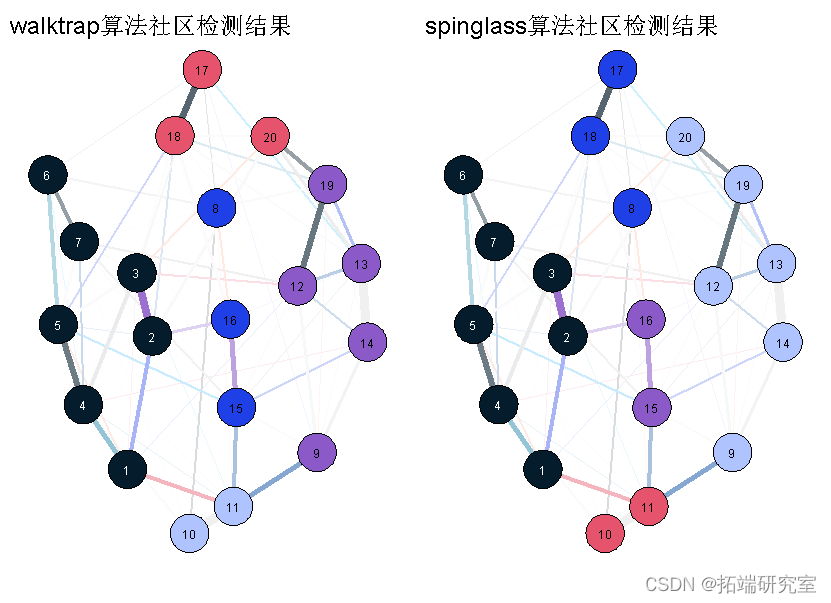
正如你现在看到的，在这个可视化中，不清楚节点8应该属于蓝色还是红色社区，我们没有明确的直观偏好。
结论
如果你对网络中的项目之间的统计社区感兴趣，不要只在视觉上检查你的图。当我为论文做这件事时，我使用上面描述的三种方法，通常它们的结果相当相似。显然，你也可能对理论或概念更感兴趣。在这种情况下，你可能根本不需要看你的数据，不需要经历上述所有的麻烦。
请注意，上述spinglass或walktrap等社群检测方法的最大局限是，项目确定地只属于一个社群。对于心理学数据来说，拟合因子模型经常会发现有交叉负荷的项目，这是一个问题。而你可以通过模拟一个2因子模型看到，其中1个项目在两个因子上都有同样的载荷。希望我们很快就能在R中实现允许项目同时属于多个社区的算法（Barabási在他的《网络科学》一书第9章中描述了几个。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
LSTM神经网络结合PSO粒子群优化对管网优化调度及网络安全入侵检测模型|附数据代码
Python复杂网络社区检测：并行谱聚类算法设计与多种算法应用实战研究
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
R语言SVM模型用大学生行为数据对助学金精准资助预测ROC可视化
