确定数据集中最佳的簇数是分区（划分）聚类（例如k均值聚类）中的一个基本问题，它要求用户指定要生成的簇数k。
一个简单且流行的解决方案包括检查使用分层聚类生成的树状图，以查看其是否暗示特定数量的聚类。不幸的是，这种方法也是主观的。
可下载资源
我们将介绍用于确定k均值，k medoids（PAM）和层次聚类的最佳聚类数的不同方法。
这些方法包括直接方法和统计测试方法：
聚类有效性的评价标准有两种：一是外部标准，通过测量聚类结果和参考标准的一致性来评价聚类结果的优良；另一种是内部指标，用于评价同一聚类算法在不同聚类数条件下聚类结果的优良程度，通常用来确定数据集的最佳聚类数。
轮廓系数Average silhouette method
轮廓系数是类的密集与分散程度的评价指标。
a(i)是测量组内的相似度,b(i)是测量组间的相似度，s(i)范围从-1到1，值越大说明组内吻合越高，组间距离越远——也就是说，轮廓系数值越大，聚类效果越好
可以看到也是在聚类数为3时轮廓系数达到了峰值，所以最佳聚类数为3
Gap Statistic
之前我们提到了WSSE组内平方和误差，该种方法是通过找“肘点”来找到最佳聚类数，肘点的选择并不是那么清晰，因此斯坦福大学的Robert等教授提出了Gap Statistic方法，定义的Gap值为[9]
取对数的原因是因为Wk的值可能很大 通过这个式子来找出Wk跌落最快的点，Gap最大值对应的k值就是最佳聚类数
可以看到也是在聚类数为3的时候gap值取到了最大值，所以最佳聚类数为3
层次聚类
层次聚类是通过可视化然后人为去判断大致聚为几类，很明显在共同父节点的一颗子树可以被聚类为一个类
Affinity propagation (AP) clustering
这个本质上是类似kmeans或者层次聚类一样，是一种聚类方法，因为不需要像kmeans一样提供聚类数，会自动算出最佳聚类数，因此也放到这里作为一种计算最佳聚类数目的方法。 AP算法的基本思想是将全部样本看作网络的节点，然后通过网络中各条边的消息传递计算出各样本的聚类中心。聚类过程中，共有两种消息在各节点间传递，分别是吸引度( responsibility)和归属度(availability) 。AP算法通过迭代过程不断更新每一个点的吸引度和归属度值，直到产生m个高质量的Exemplar（类似于质心），同时将其余的数据点分配到相应的聚类中
选x或者y方向看(对称)，可以数出来“叶子节点”一共15个
Calinsky criterion
这个评估标准定义如下： 其中，k是聚类数，N是样本数，SSw是我们之前提到过的组内平方和误差， SSb是组与组之间的平方和误差，SSw越小，SSb越大聚类效果越好，所以Calinsky criterion值一般来说是越大，聚类效果越好
可以看到在聚类数目为3时，calinski指标达到了最大值，所以最佳数目为3
组内平方误差和——拐点图
想必之前动辄几十个指标，这里就用一个最简单的指标——sum of squared error (SSE)组内平方误差和来确定最佳聚类数目。这个方法也是出于《R语言实战》，自定义的一个求组内误差平方和的函数。
随着聚类数目增多，每一个类别中数量越来越少，距离越来越近，因此WSS值肯定是随着聚类数目增多而减少的，所以关注的是斜率的变化，但WWS减少得很缓慢时，就认为进一步增大聚类数效果也并不能增强，存在得这个“肘点”就是最佳聚类数目，从一类到三类下降得很快，之后下降得很慢，所以最佳聚类个数选为三
参考文献[1]R语言实战第二版 [2]Partitioning cluster analysis: Quick start guide – Unsupervised Machine Learning [3]BIC：http://www.stat.washington.edu/raftery/Research/PDF/fraley1998.pdf [4]Cluster analysis in R: determine the optimal number of clusters [5]Calinski-Harabasz Criterion：Calinski-Harabasz criterion clustering evaluation object [6]Determining the optimal number of clusters: 3 must known methods – Unsupervised Machine Learning [7] affinity-propagation：聚类算法Affinity Propagation(AP) [8]轮廓系数https://en.wikipedia.org/wiki/Silhouette(clustering)) [9]gap statistic-Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2001, 63(2): 411-423. [10]ClustergramsClustergram: visualization and diagnostics for cluster analysis (R code)
- 直接方法：包括优化准则，例如簇内平方和或平均轮廓之和。相应的方法分别称为弯头方法和轮廓方法。
- 统计检验方法：包括将证据与无效假设进行比较。
除了肘部，轮廓和间隙统计方法外，还有三十多种其他指标和方法已经发布，用于识别最佳簇数。我们将提供用于计算所有这30个索引的R代码，以便使用“多数规则”确定最佳聚类数。
对于以下每种方法：
- 我们将描述基本思想和算法
- 我们将提供易于使用的R代码，并提供许多示例，用于确定最佳簇数并可视化输出。
肘法
回想一下，诸如k-均值聚类之类的分区方法背后的基本思想是定义聚类，以使总集群内变化[或总集群内平方和（WSS）]最小化。总的WSS衡量了群集的紧凑性，我们希望它尽可能小。
Elbow方法将总WSS视为群集数量的函数：应该选择多个群集，以便添加另一个群集不会改善总WSS。
最佳群集数可以定义如下：
- 针对k的不同值计算聚类算法（例如，k均值聚类）。例如，通过将k从1个群集更改为10个群集。
- 对于每个k，计算群集内的总平方和（wss）。
- 根据聚类数k绘制wss曲线。
- 曲线中拐点（膝盖）的位置通常被视为适当簇数的指标。
平均轮廓法
平均轮廓法计算不同k值的观测值的平均轮廓。聚类的最佳数目k是在k的可能值范围内最大化平均轮廓的数目（Kaufman和Rousseeuw 1990）。
差距统计法
该方法可以应用于任何聚类方法。
间隙统计量将k的不同值在集群内部变化中的总和与数据空引用分布下的期望值进行比较。最佳聚类的估计将是使差距统计最大化的值（即，产生最大差距统计的值）。
资料准备
我们将使用USArrests数据作为演示数据集。我们首先将数据标准化以使变量具有可比性。
head(df)
## Murder Assault UrbanPop Rape
## Alabama 1.2426 0.783 -0.521 -0.00342
## Alaska 0.5079 1.107 -1.212 2.48420
## Arizona 0.0716 1.479 0.999 1.04288
## Arkansas 0.2323 0.231 -1.074 -0.18492
## California 0.2783 1.263 1.759 2.06782
## Colorado 0.0257 0.399 0.861 1.86497Silhouhette和Gap统计方法
简化格式如下：
下面的R代码确定k均值聚类的最佳聚类数：
# 肘部法
fviz_nbclust(df, kmeans, method = "wss") +
geom_vline(xintercept = 4, linetype = 2)+
labs(subtitle = "Elbow method")
# Silhouette 方法
# Gap 统计量
## Clustering k = 1,2,..., K.max (= 10): .. done
## Bootstrapping, b = 1,2,..., B (= 50) [one "." per sample]:
## .................................................. 50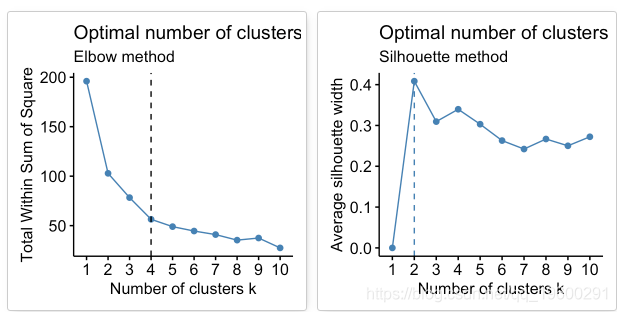
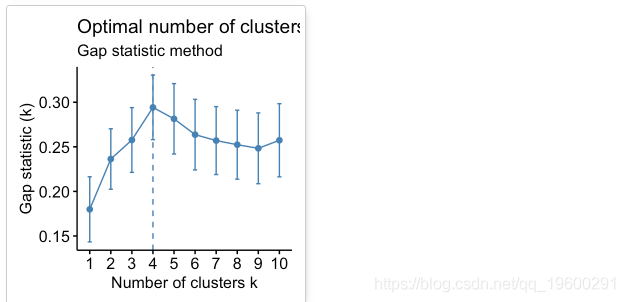
根据这些观察，有可能将k = 4定义为数据中的最佳簇数。
30个索引，用于选择最佳数目的群集
数据：矩阵
- diss：要使用的相异矩阵。默认情况下，diss = NULL，但是如果将其替换为差异矩阵，则距离应为“ NULL”
- distance：用于计算差异矩阵的距离度量。可能的值包括“ euclidean”，“ manhattan”或“ NULL”。
- min.nc，max.nc：分别为最小和最大簇数
- 要为kmeans 计算NbClust（），请使用method =“ kmeans”。
- 要计算用于层次聚类的NbClust（），方法应为c（“ ward.D”，“ ward.D2”，“ single”，“ complete”，“ average”）之一。
下面的R代码为k均值计算：
## Among all indices:
## ===================
## * 2 proposed 0 as the best number of clusters
## * 10 proposed 2 as the best number of clusters
## * 2 proposed 3 as the best number of clusters
## * 8 proposed 4 as the best number of clusters
## * 1 proposed 5 as the best number of clusters
## * 1 proposed 8 as the best number of clusters
## * 2 proposed 10 as the best number of clusters
##
## Conclusion
## =========================
## * According to the majority rule, the best number of clusters is 2 .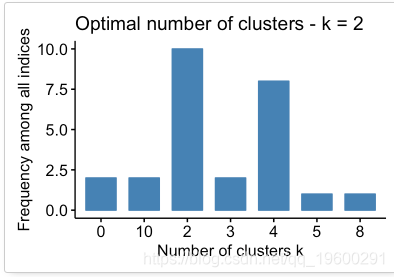
根据多数规则，最佳群集数为2。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python量子计算聚类Q-means（量子k-means）算法分析电路数据实现可视化
TensorFlow深度学习框架改进K-means聚类、SOM自组织映射神经网络算法及上海招生政策影响分析研究
Python回归、聚类、相关分析上海公租房租金满意度影响因素数据可视化
Python对历年高考分数线数据用聚类、决策树可视化分析一批、二批高校专业、位次、计划人数数据|附代码数据
