在本文中我们对在Google趋势上的关键字“ Chocolate ”序列进行预测。
序列如下
可下载资源
> report = read.csv(url,skip=6,header=FALSE,nrows=636)
> plot(X,type="l")
每月建立一个ARIMA模型比每周建立一个容易。因此，我们将每月数据序列化，将预测与观察结果进行比较。
> Y = tapply(base$X,as.factor(base$AM),mean)
> Z = ts(as.numeric(Y[1:(146-24)]), start=c(2004,1),frequency=12)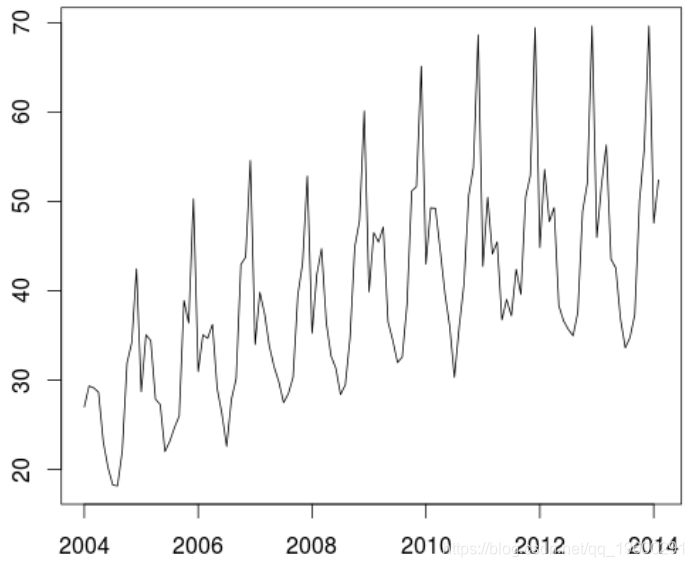
在这里转换序列的对数序列。我们观察到趋势的变化（开始时是线性的，此后相对稳定）。
> X=log(as.numeric(Z))
> trend=lm(X~T+I((T-80)*(T>80)),data=db)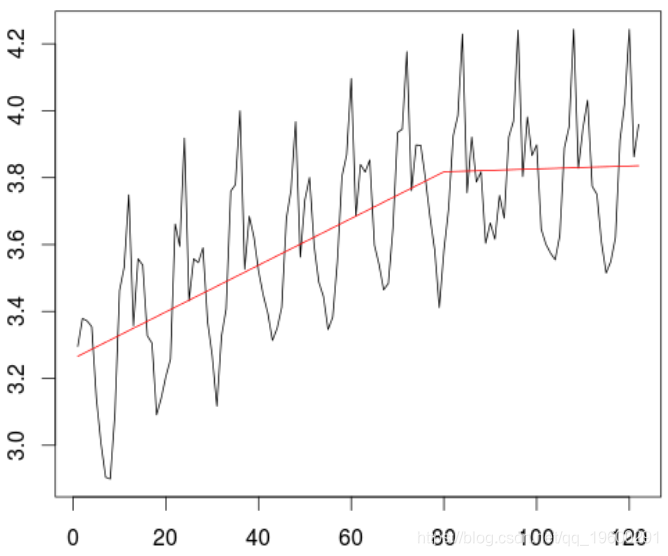
这是我们要建模的序列残差，
residuals(trend)
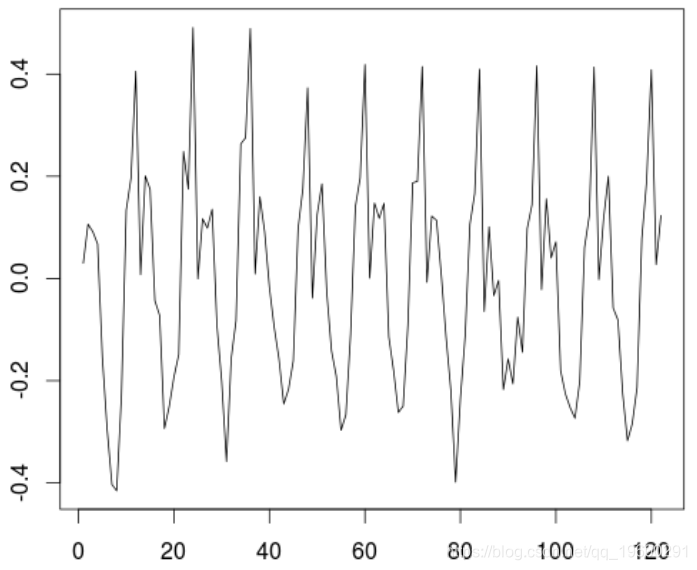
要对该序列进行建模，我们可以先查看其自相关序列
> plot(acf(Y,lag=36),lwd=5)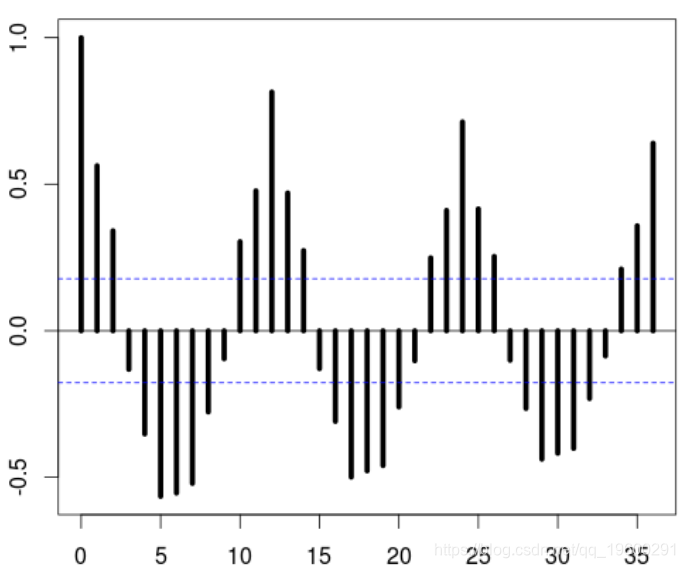
和偏自相关序列
> plot(pacf(Y,lag=36),lwd=5)
该序列是稳定的，但是有很强的周期性成分。
我们可以尝试AR模型或ARMA（带有AR的残差不是白噪声）。
arima(Y,order=c(12,0,12),
+ seasonal = list(order = c(0, 0, 0 , period = 12 )这里的残差序列是白噪声
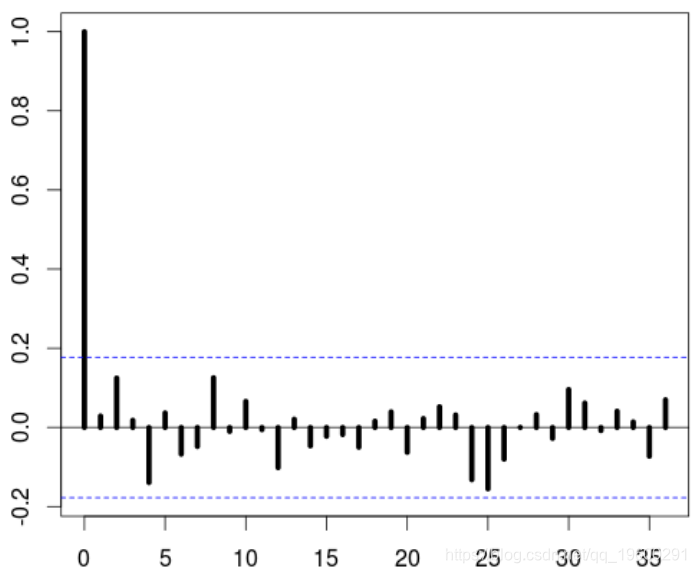
随时关注您喜欢的主题
然后，我们可以使用此模型对初始序列进行预测
> Y2=tapply(base$X,as.factor(base$AM),mean)
> lines(futur,obs_reel,col="blue")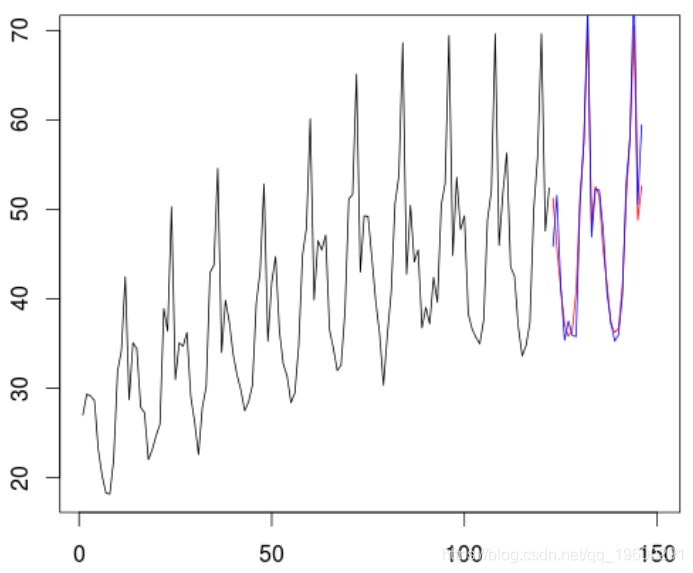 
我们的模型为红色，真实的观察结果为蓝色。然后，我们可以根据这24个观测值计算。
误差平方和。
> sum( (obs_reel-Xp)^2 )
[1] 190.9722但是我们可以尝试其他模型，例如通过更改趋势或通过更改ARIMA模型（通过季节性单位根）来尝试
> E=residuals(model3)
> model3
Coefficients:
ma1 ma2 sma1
0.2246 0.3034 -0.9999
s.e. 0.0902 0.0925 0.3503
sigma^2 estimated as 0.002842: log likelihood = 152.37, aic = -296.75我们检查残差序列确实是白噪声
Box-Pierce test
data: E
X-squared = 6.326, df = 12, p-value = 0.8988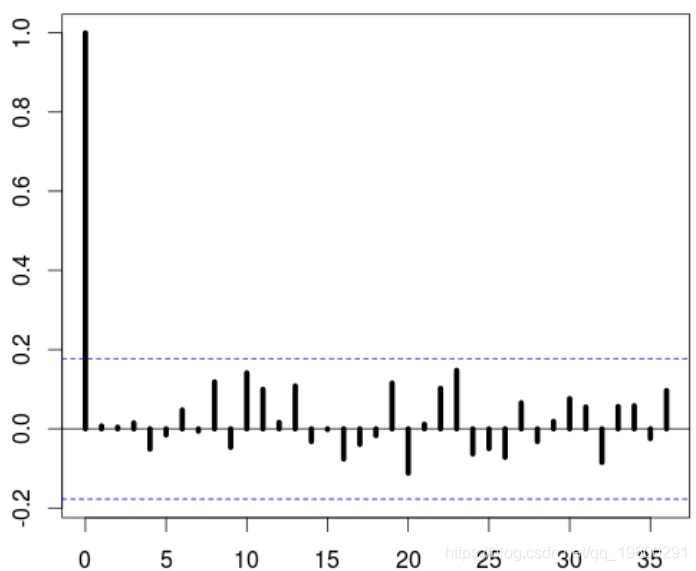
然后，我们可以对原始系列进行预测，
> Yp=predict(model3,n.ahead=24) +
+ predict(trend,newdata=data.frame(T=futur)
> Y2=tapply( X,as.factor( AM),mean)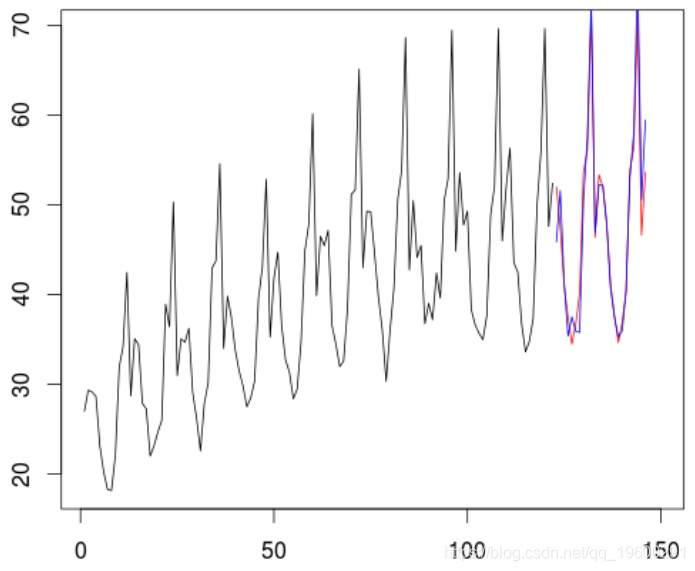
误差平方和低一些
> sum( (obs_reel-Xp)^2 )
[1] 173.8138也就是说，在过去的两年中，第二个模型比以前的模型要好，是对未来几年进行预测的好方法。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
【梯度提升专题】XGBoost、Adaboost、CatBoost预测合集：抗乳腺癌药物优化、信贷风控、比特币应用|附数据代码
【专题】2024年快消市场全域发展图景和趋势展望报告汇总PDF洞察（附原数据表）
