为了在统计过程中发现更多有趣的结果，我们将解决极大似然估计没有简单分析表达式的情况。
举例来说，如果我们混合了各种分布，
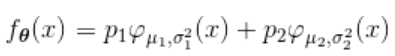
可下载资源
作为说明，我们可以使用样例数据
> X=height第一步是编写混合分布的对数似然函数
极大似然估计是在已知样本服从某种概率分布，但不知道概率分布的具体参数（比如均值、方差等）情况下，通过大量的数据或试验，基于概率最大化来推出参数的大概值。
但是极大似然估计使用需要一定的条件，在实际中我们可能会遇到观测数据不完善，存在缺失数据或者隐含变量的情况，这时候EM算法就发挥了作用。比如目前网上介绍EM算法常用的例子：男女身高分布，在甚至不知道每一个样本是男还是女的情况下，先赋予男、女概率分布参数（均值、方差）初始值，根据初始值求期望（E步）算出每一个样本可能是男还是女，基于此，在初步算出每一样本来自男还是女的条件下，采用极大似然估计来求概率分布参数（M步），如此循环、迭代，最终根据一定的收敛法则找到参数值。
02
其实，EM算法就是在极大似然估计多了一个隐含变量所采用的先猜再求后迭代的多次尝试算法，在这里举一个更简单的例子，它不仅展示了EM算法对于极大似然估计存在缺失数据或隐含变量的解决办法，也展示了EM算法与极大似然估计的另一个关系：在似然函数不是显然的，或者函数的形式非常复杂导致难以用极大似然传统方法进行估计等情况下，EM算法作为一种数据增广算法的一种迭代优化策略。
> logL=function(theta){
+ p=theta[1]
+ m1=theta[2]
+ s1=theta[3]
+ m2=theta[4]
+ s2=theta[5]
+ logL=-sum(log(p*dnorm(X,m1,s1)+(1-p)*dnorm(X,m2,s2)))
+ return(logL)
+ }极大似然性的最简单函数如下（从一组初始参数开始，只是为了获得梯度下降的起点）
> optim(c(.5,160,1,180,1 ,logL > theta=opt$par)
[1] 0.5987635 165.2547700 5.9410993 178.4856961 6.3547038因为我们可以通过使用约束优化算法来做到“更好”，例如，概率一定在0到1之间。
为了可视化估计的密度，我们使用
> hist(X,col="light green probability=TRUE)
> lines(density(X )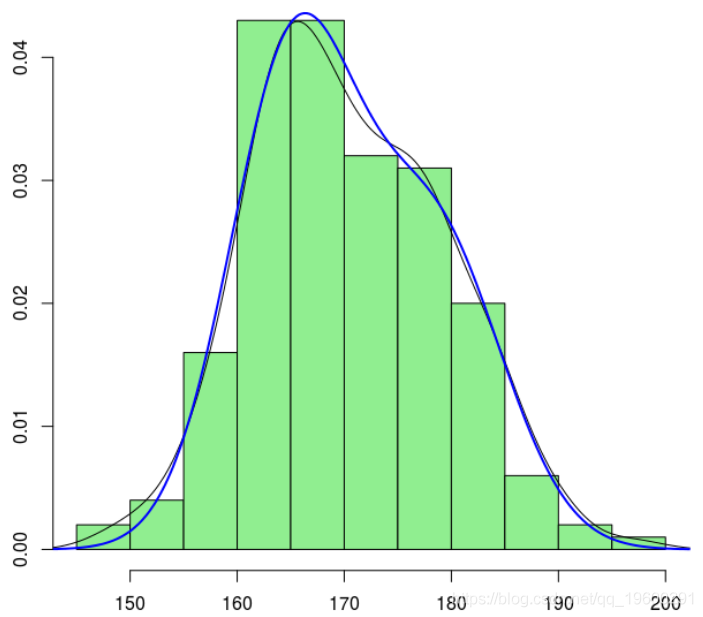
另一个解决方案是使用EM算法。我们将从参数的初始值开始，并比较属于每个类的机会
> p=p1/(p1+p2)从属于每个类别的这些概率中，我们将估算两个正态分布的参数。使用极大似然
> m1=sum(p*X)/sum(p)
+ logL=-sum(log(p*dnorm(X,m1,s1)+(1-p)*dnorm(X,m2,s2)))
+ return(logL)这个想法实际上是有一个循环的：我们估计属于这些类的概率（考虑到正态分布的参数），一旦有了这些概率，就可以重新估计参数。然后我们再次开始
> for(s in 1:100){
+ p=p1/(p1+p2)
+ s1=sqrt(sum(p*(X-m1)^2)/sum(p))
+ s2=sqrt(sum((1-p)*(X-m2)^2)/sum(1-p))
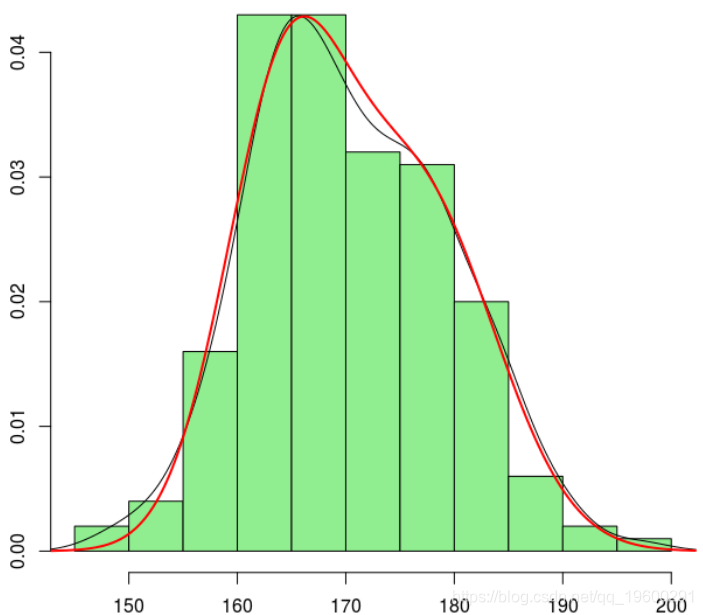
+ }然后，我们恢复混合分布的“最佳”参数
> hist(X,col="light green",probability=TRUE)
> lines(density(X))这相对接近我们的估计。
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
SAS数据挖掘EM贷款违约预测分析：逐步Logistic逻辑回归、决策树、随机森林
R语言代做编程辅导和解答GLM Coursework
