R语言混合图形模型MGM的网络可预测性分析

网络模型已经成为抽象复杂系统，是深入了解许多科学领域中观测变量之间的关系模式的流行方法。

由Kaizong Ye，Sherry Deng撰写

最近我们被客户要求撰写关于网络可预测性的研究报告。这些应用程序大多数集中于分析网络的结构。但是，如果不是直接观察网络，而是根据数据进行估算（如：吸烟与癌症之间存在关联），则除了网络结构外，我们还可以分析网络中节点的可预测性。

当我们不直接观察网络本身，而是依赖数据来估算和理解网络中的关联和交互时，除了分析网络的结构特性，节点的可预测性同样是一个至关重要的方面。在这种情况下，数据成为了我们洞察网络动态和节点行为的关键工具。

节点的可预测性主要指的是根据已有数据和信息，预测网络中特定节点未来状态或行为的能力。在复杂网络中，每个节点可能代表一个实体（如人、组织或事件），而节点之间的连接则反映了这些实体之间的相互作用或关系。通过分析节点的历史数据和行为模式，我们可以揭示出节点的潜在规律，并据此预测其未来的变化。

也就是说：网络中的所有其余节点如何预测网络中的给定节点？

可预测性有趣，有几个原因：

它给我们提供了一个关于边的实用性的想法：如果节点A连接到许多其他节点，但是这些仅说明（假设）其方差的1％，那么边的连接会是怎样的？
它告诉我们网络的不同部分在多大程度上是由网络中的其他因素决定的

可下载资源

完整程序、数据和文档（word）

作者

Kaizong Ye
✉ 联系我们

在此博文中，我们使用R-估计网络模型并计算地震灾民数据集上的创伤后应激障碍（PTSD）症状。我们对网络模型和可预测性进行可视化，并讨论如何将网络模型和节点的可预测性相结合来设计症状网络的有效干预措施。

对社会网络链接预测的现有研究方法主要集中在基于概率模型、基于监督学习和基于相似度三类。

基于相似性的算法是链接预测中最直接有效的方法，但是也具有很多的挑战性。比如节点相似性的定义本身就存在异议，相似性指数的分类更是复杂。相似性通常是通过两个节点之间的共同特征来衡量，共同特征越多，相似性越高，则越有可能存在链接。然而通常情况下，能够直接得到的是网络拓扑结构，节点的属性是隐藏的，纯粹基于拓扑结构的相似性指数往往是比较浅显的，因而基于结构相似性的链接预测准确率高低，往往与结构相似性所提出的指标以及目标网络所具有的拓扑特性的匹配程度相关。

基于监督学习的链接预测主要是根据特征值对节点进行分类，这样链接预测就是一个典型的二分分类问题，但是这种方法的难点在于特征值的选取，通常做法是以图的拓扑结构来寻找特征值。

虽然很多研究表明，借助于节点属性的链接预测具有比较好的效果，但是这些属性往往是被看作独立的，于是有部分研究者考虑把节点属性进行有效结合，看是否对链接预测的准确性会有提高，这就产生了基于概率模型的方法，这类方法是系统的将节点和边属性进行结合，构造出一种联合概率分布，得到结构化的数据关系。

载入资料

我们加载提供的数据：

 
data <- as.matrix(data)
p <- ncol(data)
dim(data)

## [1] 312  17

数据集包含对344人的17种PTSD症状的完整反应。症状强度的答案类别范围从1“没有”到5“非常强”。

估计网络模型

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

我们估计了混合图形模型，其中我们将所有变量都视为连续高斯变量。因此，我们将所有变量的类型设置为，type = 'g'并将每个变量的类别数设置为1：

 
fit_obj <- (data = data, 
               type = rep('g', p),
               level = rep(1, p),
               lambdaSel = 'CV',
               ruleReg = 'OR', 
               pbar = FALSE)

计算节点的可预测性

估计网络模型后，我们准备计算每个节点的可预测性。由于可以通过依次获取每个节点并对其上的所有其他节点进行回归来估计该图，因此可以轻松地计算节点的可预测性）。

作为可预测性的度量，我们选择解释的方差的比例：0表示当前节点根本没有被节点中的其他节点解释，1表示完美的预测。我们在估算之前将所有变量中心化，以消除截距的影响。

有关如何计算预测和选择可预测性度量的详细说明，请查看本文。如果网络中还有其他变量类型（例如分类），我们可以为这些变量选择适当的度量。

pred_obj <- predict(object = fit_obj, 
                    data = data
 
pred_obj$error

##     Variable    R2
## 1  intrusion 0.639
## 2     dreams 0.661
## 3      flash 0.601
## 4      upset 0.636
## 5    physior 0.627
## 6    avoidth 0.686
## 7   avoidact 0.681
## 8    amnesia 0.410
## 9    lossint 0.520
## 10   distant 0.498
## 11      numb 0.451
## 12    future 0.540
## 13     sleep 0.565
## 14     anger 0.562
## 15    concen 0.638
## 16     hyper 0.676
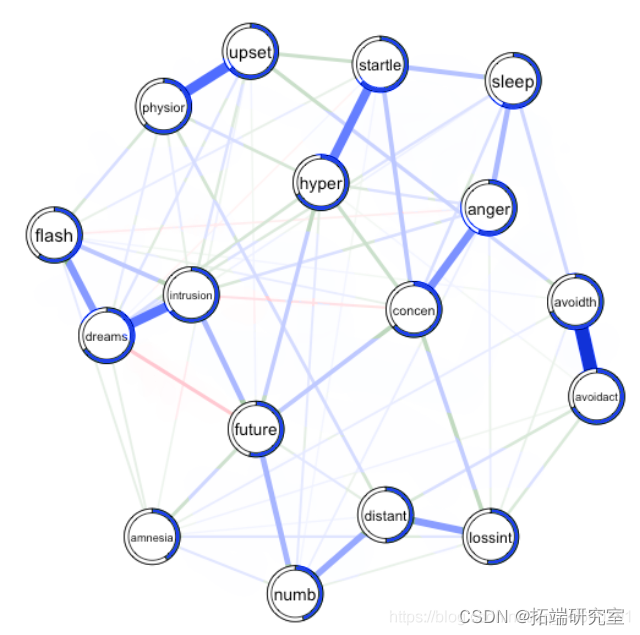
## 17   startle 0.626

我们计算了网络中每个节点的解释方差（R2）的百分比。接下来，我们将估计的网络可视化，并讨论与解释方差有关的结构。

最受欢迎的见解

1.采用spss-modeler的web复杂网络对所有腧穴进行分析

2.用R语言和python进行社交网络中的社区检测

3.R语言文本挖掘NASA数据网络分析，tf-idf和主题建模

4.在R语言中使用航空公司复杂网络对疫情进行建模

5.python隶属关系图模型基于模型的网络中密集重叠社区检测

6.使用Python和SAS Viya分析社交网络

7.关联网络分析：已迁离北京外来人口的数据画像

8.情感语义网络：游记数据感知旅游目的地形象

9.用关联规则数据挖掘探索药物配伍中的规律

可视化网络和可预测性

我们根据估计的加权邻接矩阵和节点的可预测性度量作为参数，进行网络可视化：

 
graph(fit_obj$pairwise$wadj, # 加权邻接矩阵作为输入
       layout = 'spring', 
       pie = pred_obj$error[,2], # 误差作为饼图的输入

有关早期研究不同心理障碍症状可预测性的文章，请参见本文。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！