
在事物的发展过程中,常表现出复杂的波动情况,即时而波动的幅度较缓,而又时常出现波动集聚性(VolatilitY clustering),在风险研究中经常遇到这种情况。
恩格尔(Engle)在1982年提出了用来描述方差波动的自回归条件异方差模型ARCH (Autoregressive conditional heteroskedasticity model )。
并由博勒斯莱 文(Bollerslev, T., 1986)发展成为广义自回归条件异方 差GARCH (Generalized ARCH),后来又发展成为很多的特殊形式。
可下载资源
在AR(1)过程的背景下,我们花了一些时间来解释当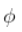 接近于1时会发生什么。
接近于1时会发生什么。
- 如果
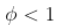 过程是平稳的,
过程是平稳的, - 如果
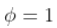 该过程是随机游走
该过程是随机游走 - 如果
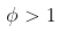 这个过程会大幅波动
这个过程会大幅波动
ARCH模型的英文直译是:自回归条件异方差模型。
是一种用来处理时间序列的模型。在股票中,ARCH可以用来预测股票的波动率,从而控制风险。(在金融领域,波动率与风险直接挂钩,一个资产波动越大,风险越大,而获得更高收益的可能也更大)
ARCH模型广泛应用于波动性有关广泛研究领域。包括政策研究、理论命题检验、季节性分析等方面。
要了解这是一种怎样的模型,我们可以从这个名字入手:自回归、条件异方差。
自回归
回归分析,是我们经常用到的统计模型。
我们经常用回归分析来解释一些事物的变化,用的最多的是线性回归,可以帮助我们找到一些事物之间的相关系。
举个简单的例子:
身高=70%遗传因素+30%后天因素
在这个简单的公式中,就用到了回归分析,身高可以被遗传因素和后天因素两种因素解释,我们还找到了他们各自的比重:如果你的个子不高,那就要努力提高下一代的后天因素了。
这就是一个回归。那自回归呢,我们可以理解为自己与自己的回归,在时间序列上,也就是昨天的你、前天的你,对今天的你的影响。
今天的身高=a昨天的身高+b前天的身高+c*前两天的身高+……
因为,用到的因素都是你自己,只是时间不同,所以这种回归叫做自回归。
自回归模型,是统计上一种处理时间序列的方法,是用同一变量之前各期的表现情况,来预测该变量本期的表现情况,并假设它们为线性关系。因为这是从回归分析中的线性回归发展而来,只是不是用来预测其他变量,而是用来预测自己,所以叫做自回归。
随机扰动项
昨天的你,前天的你,都可以用来预测今天的你,只是预测的结果是否准确,受到很多因素的影响。
也许,你的身高变化不仅受到自己的影响,还受到气候、家庭,甚至空气、水源的影响,但是在你刚刚建立的模型中,他们都是被忽略掉的。
他们藏在了一个地方:随机扰动项。
今天的身高=昨天的身高+b前天的身高+c*前期天的身高+……随机扰动项
也许根据你的模型,你今天应该达到1.70,但是你只有1.65,那就是你的模型中可能有些因素被你忽略掉了,它也对你的身高有影响,它就是随机扰动项。
异方差
由于随机扰动项包含了所有无法用解释变量表示的各种因素对被解释变量的影响,即模型中略去的经济变量对被解释变量的影响。
如果其中被略去的某一因素或某些因素随着解释变量观测值的不同而对被解释变量产生不同的影响,就会使随机扰动项产生异方差性。
你可以这样理解,如果你的身高,受到昨天、前天的身高的影响,而这个随机扰动项也受到昨天、前天身高的影响,那这个扰动项也会随着每天的数据变化,这就是异方差。
异方差一般可归结为三种类型:
(1) 单调递增型:随X的增大而增大,即在X与Y的散点图中,表现为随着X的增大Y值的波动越来越大。
(2)单调递减型:随X的增大而减小,即在X与Y的散点图中,表现为随着X值的增大Y值得波动越来越小。
(3)复杂型:与X的变化呈复杂形式,即在X与Y的散点图中,表现为随着X值的增大Y值的波动复杂多变没有系统关系。
同样,随机游走是非常有趣的过程,具有令人费解的特性。例如,
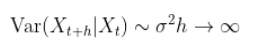
作为 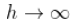 ,并且该过程将无限次穿过 _x_轴……
,并且该过程将无限次穿过 _x_轴……
我们仔细研究了 ARCH(1) 过程的性质,尤其是当 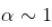 ,我们得到的结果可能令人费解。
,我们得到的结果可能令人费解。
考虑一些 ARCH(1) 过程 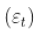 ,具有高斯噪声,即
,具有高斯噪声,即
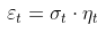
其中
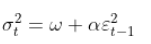
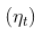 是一个 iid 序列
是一个 iid 序列 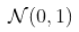 变量。这里
变量。这里 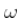 和
和 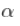 必须是正的。
必须是正的。
回顾 由于 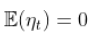
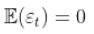 . 因此
. 因此
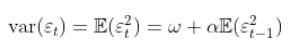
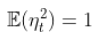 ,所以方差存在,并且只有当
,所以方差存在,并且只有当 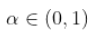 , 在这种情况下
, 在这种情况下
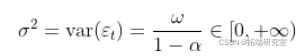
此外,如果 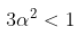 ,则可以得到第四矩,
,则可以得到第四矩,
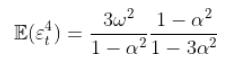
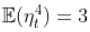 . 现在,如果我们回到研究方差时获得的属性,如果
. 现在,如果我们回到研究方差时获得的属性,如果 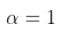 , 或者
, 或者 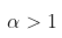 ?
?
如果我们查看模拟,我们可以生成一个 ARCH(1) 过程 , 例如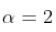 。
。
> ea=rnorm
> eson=rnorm
> sga2=rep
> for(t in 2:n){
> plot
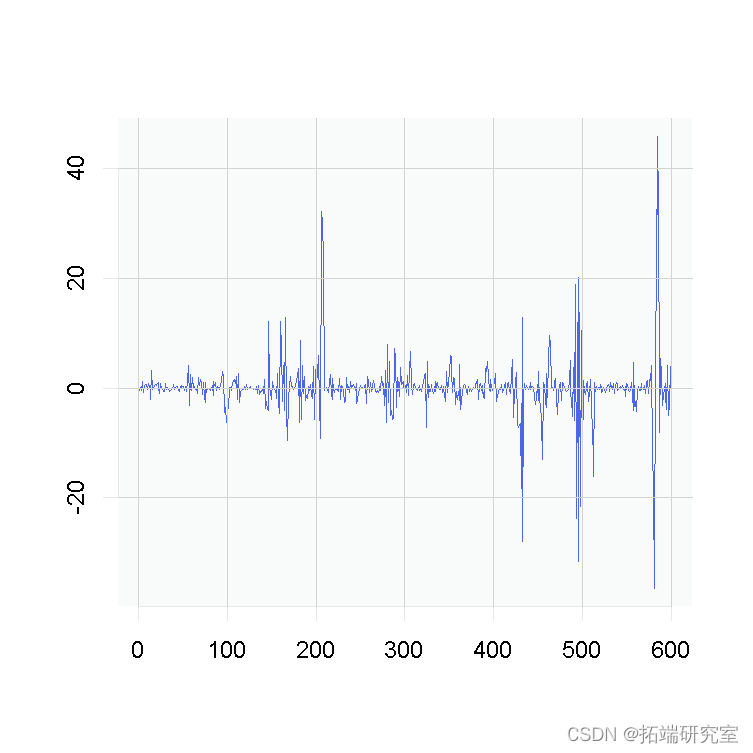
为了理解发生了什么,我们应该记住,我们好的是,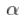 必须在
必须在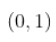 之间能够计算出
之间能够计算出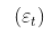 的第二时刻。 但是,有可能有一个具有无限变异的平稳过程。
的第二时刻。 但是,有可能有一个具有无限变异的平稳过程。
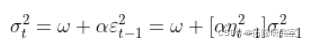
迭代
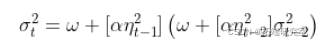
一次又一次地迭代……
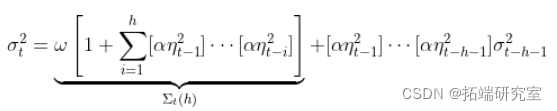
其中
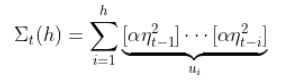
随时关注您喜欢的主题
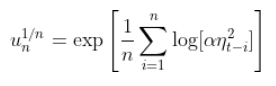
并且根据大数定律,因为我们这里有一个独立同分布项的总和,
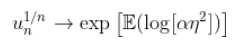
因此,如果 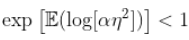 , 然后
, 然后 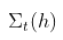 会有限制,当
会有限制,当 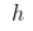 取无穷大。
取无穷大。
上面的条件可以写成
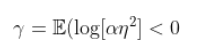
这就是所谓的 Lyapunov 系数。
方程
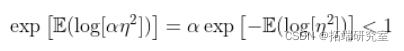
是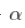 一个条件 .
一个条件 .
在这种情况下 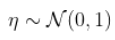 ,这个上界的数值是3.56。
,这个上界的数值是3.56。
> 1/exp(mean(log(rnorm))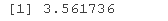
在这种情况下 (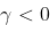 ),方差可能是无限的,但序列是平稳的。另一方面,如果
),方差可能是无限的,但序列是平稳的。另一方面,如果 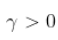 , 然后
, 然后 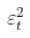 几乎肯定会走向无穷大,因为
几乎肯定会走向无穷大,因为 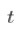 走向无穷大。
走向无穷大。
但是为了观察这种差异,我们需要大量的观察。例如, 
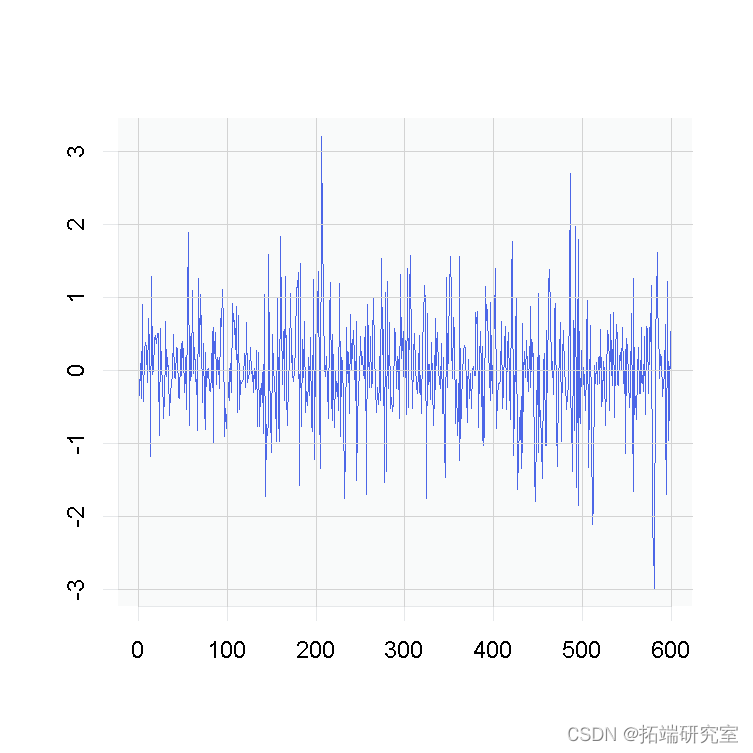
和  ,
,
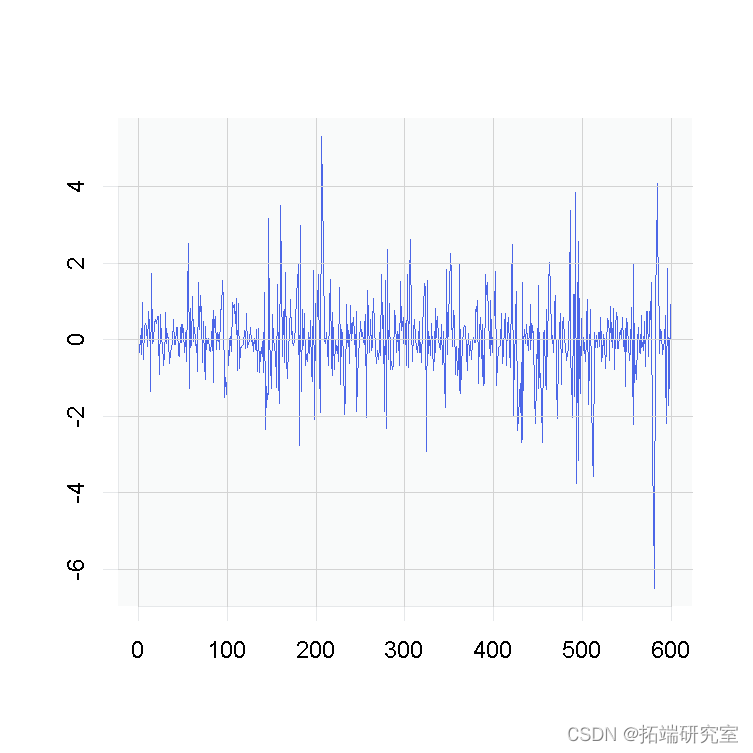
我们很容易看出区别。
我并不是说很容易看出上面的分布具有无限的方差,但仍然如此。
实际上,如果我们考虑希尔在上述系列中的图片,在正的尾巴上
实际上,如果我们考虑对上述系列的绘希尔图,在正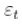 的尾部
的尾部
> hil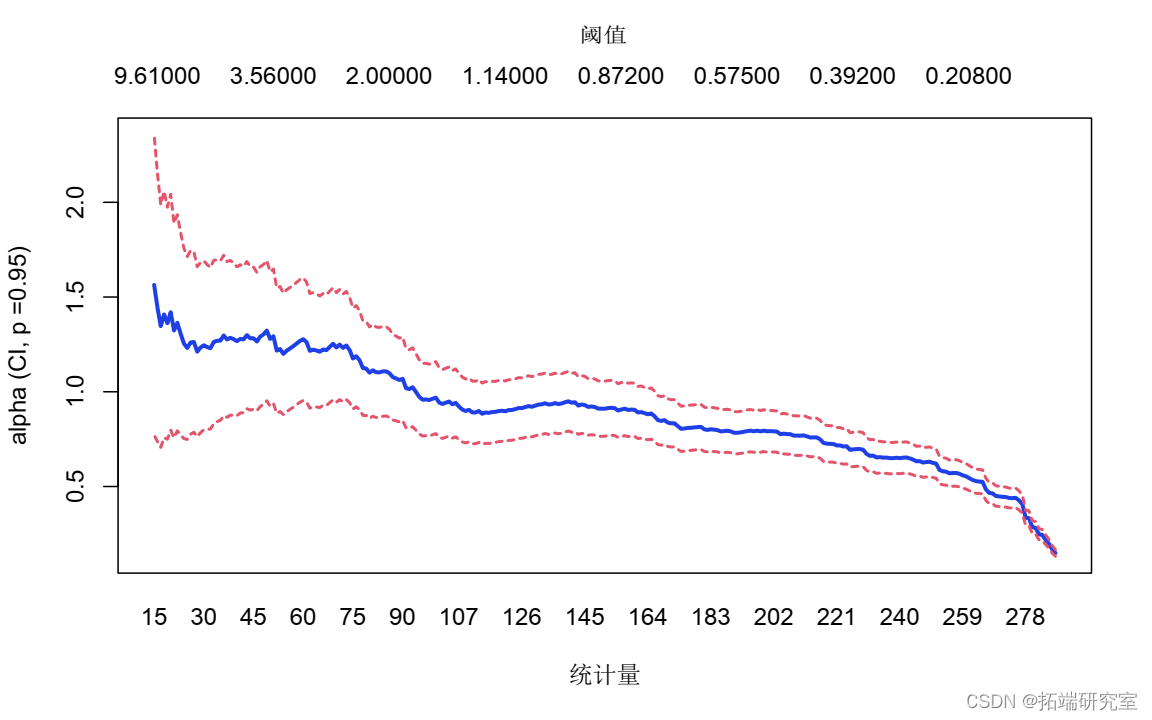
或负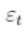 的尾部
的尾部
-epsilon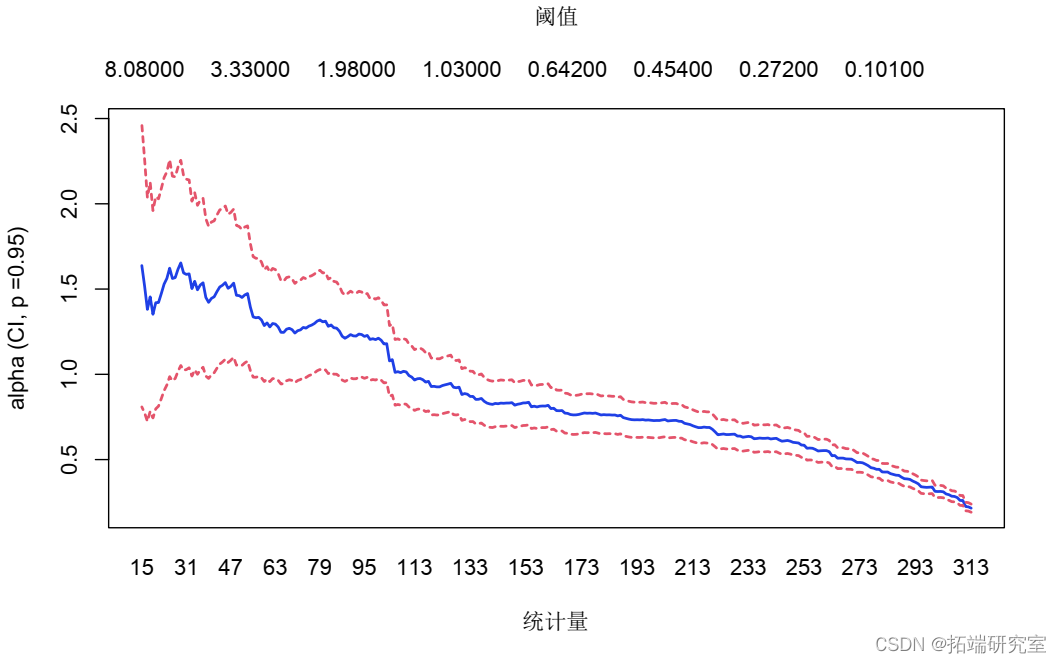
我们可以看到,尾部指数(严格来说)小于2(意味着2阶的时刻不存在)。
为什么它令人费解?也许是因为这里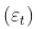 不是弱平稳(在
不是弱平稳(在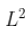 意义上),而是强平稳。这不是通常的弱和强的关系方式。这可能就是为什么我们不称其为强平稳性,而称其为严格平稳性。
意义上),而是强平稳。这不是通常的弱和强的关系方式。这可能就是为什么我们不称其为强平稳性,而称其为严格平稳性。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


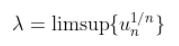
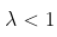 ,
, 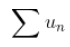 收敛。这里,
收敛。这里,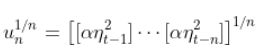
 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据 Python比特币价格时间序列:LGBMRegressor递归自回归、随机游走及外部变量预测探索
Python比特币价格时间序列:LGBMRegressor递归自回归、随机游走及外部变量预测探索



