自回归条件异方差（ARCH）模型涉及具有时变异方差的时间序列，其中方差是以特定时间点的现有信息为条件的。
ARCH模型假设时间序列模型中误差项的条件均值是常数（零），与我们迄今为止讨论的非平稳序列不同），但其条件方差不是。
ARCH模型
这样一个模型可以用公式1、2和3来描述。
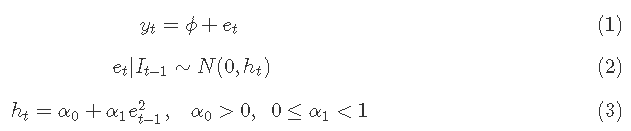
可下载资源
方程4和5给出了测试模型和假设，以测试时间序列中的ARCH效应，其中残差e^t来自于将变量yt回归一个常数，如1，或回归一个常数加上其他回归因子；方程4中的测试可能包括几个滞后项，在这种情况下，无效假设（方程5）是所有这些项都不显著。
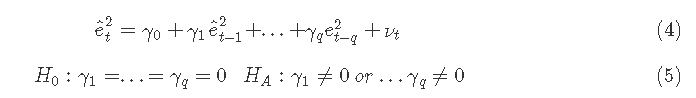
无效假设是不存在ARCH效应。检验统计量为
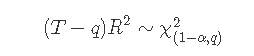
下面的例子使用了数据集，它包含了500个股票收益率的生成观测值。图显示了数据的时间序列图和柱状图。
plot.ts(r)
hist(r)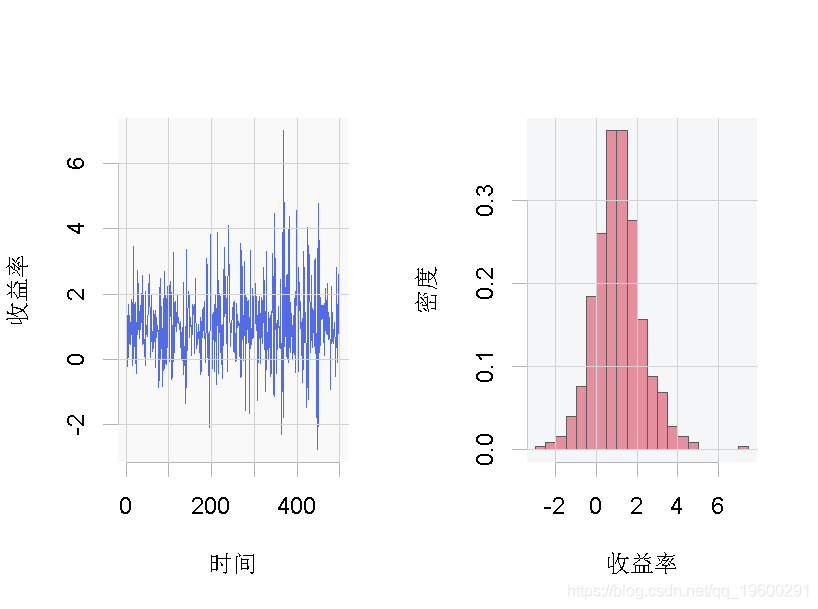
图: 变量 的水平和柱状图
让我们首先对数据集中的变量r一步一步地进行公式4和5中描述的ARCH检验。
summary(yd)
ehsq <- ts(resid(mean)^2)
summary(ARCH)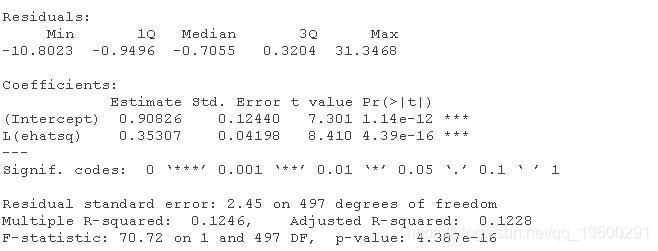
Rsq <- glance(ARCH)\[\[1\]\]
LM <- (T-q)*Rsq
Chicr <- qchisq(1-alpha, q)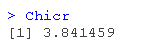
结果是LM统计量，等于62.16，与α=0.05和q=1自由度的临界卡方值进行比较；这个值是χ2(0.95,1)=3.84；这表明拒绝了无效假设，结论是该序列具有ARCH效应。
如果我们不使用一步步的程序，而是使用R的ARCH检验功能之一，也可以得出同样的结论。
ArchTest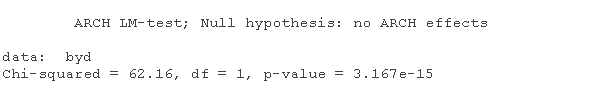
函数garch()，当使用order=参数等于c(0,1)时，成为一个ARCH模型。这个函数可以用来估计和绘制方程3中定义的方差ht，如以下代码和图所示。
garch(r,c(0,1))
随时关注您喜欢的主题
summary(arch)
ts(2*fitted.values^2)
plot.ts(hhat)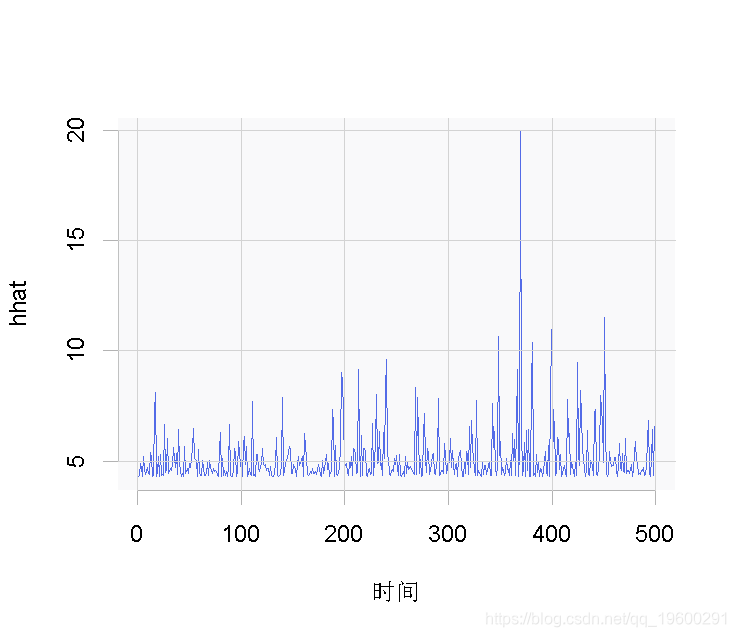
图 对数据集的ARCH(1)方差的估计
GARCH模型
# 使用软件包\`garch\`来建立GARCH模型
fit(spec=garch, data=r)
coef(Fit)
fitted.values
fit$sigma^2)
plot.ts(hhat)图: 使用数据集的标准GARCH模型（sGARCH）。
# tGARCH
garchfit(spec, data=r， submodel="TGARCH")
coef(garchfit)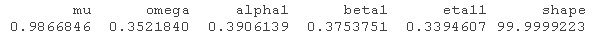
fitted.values
fit$sigma^2)
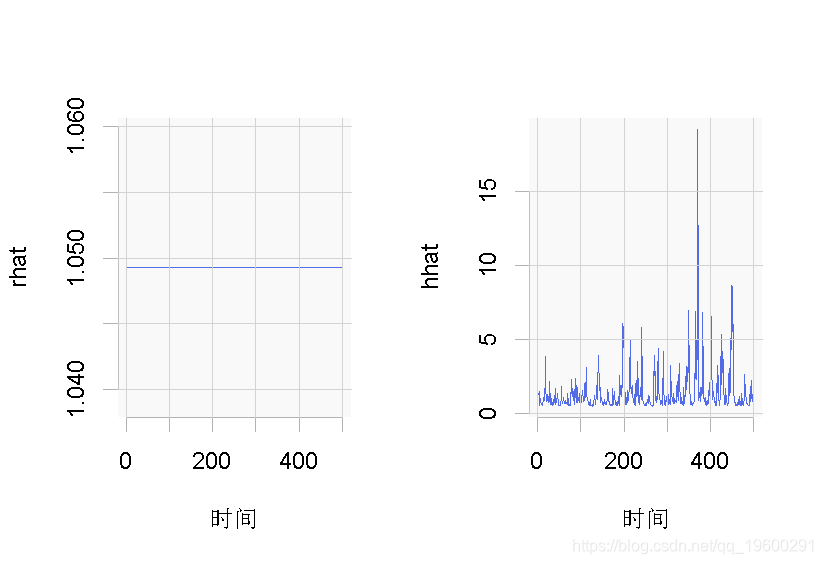
plot.ts(hhat)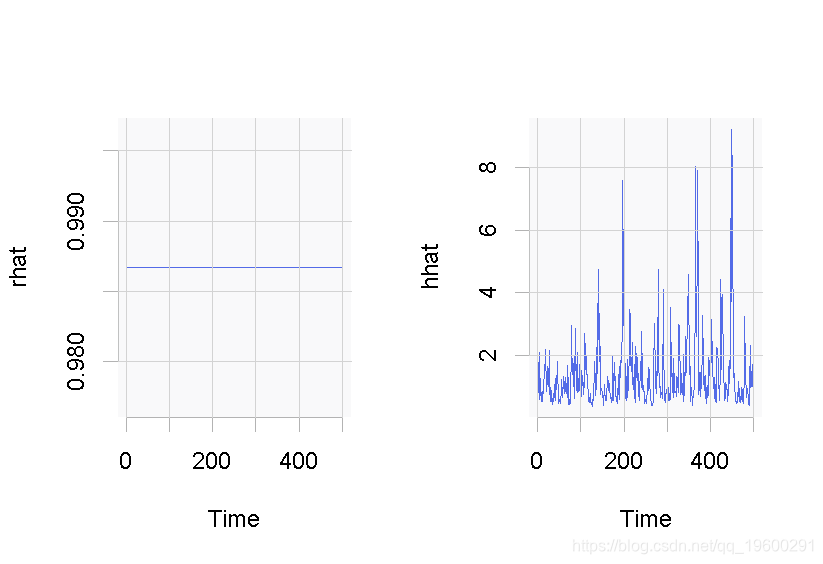
图: 数据集的tGARCH模型
# GARCH-IN-MEAN模型
fit( data=r,
distribution="std",variance=list(model="fGARCH")
coef(garchFit)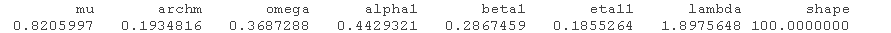
fit$fitted.values
fit$sigma^2)
plot.ts(hhat)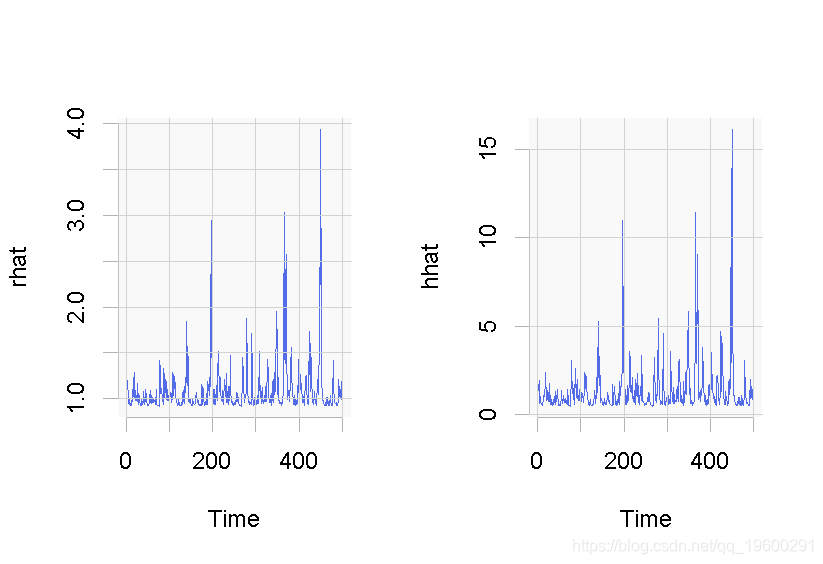
图：使用数据集的GARCH-in-mean模型的一个版本
图显示了GARCH模型的几个版本。预测结果可以通过ugarchboot()来获得。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
