神经网络一直是迷人的机器学习模型之一
不仅因为花哨的反向传播算法，而且还因为它们的复杂性（考虑到许多隐藏层的深度学习）和受大脑启发的结构。
可下载资源
最近我们被客户要求撰写关于神经网络预测的研究报告，包括一些图形和统计输出。
神经网络并不总是流行，部分原因是它们在某些情况下仍然计算成本高昂，部分原因是与支持向量机（SVM）等简单方法相比，它们似乎没有产生更好的结果。然而，最近神经网络变得流行起来。
神经网络解法
与单特征值的线性回归问题类似，多变量（多特征值）的线性回归可以被看做是一种高维空间的线性拟合。以具有两个特征的情况为例，这种线性拟合不再是用直线去拟合点，而是用平面去拟合点。
定义神经网络结构
我们定义一个一层的神经网络，输入层为2或者更多，反正大于2了就没区别。这个一层的神经网络的特点是：
1.没有中间层，只有输入项和输出层（输入项不算做一层），
2.输出层只有一个神经元，
3.神经元有一个线性输出，不经过激活函数处理，即在下图中，经过Σ求和得到Z值之后，直接把Z值输出。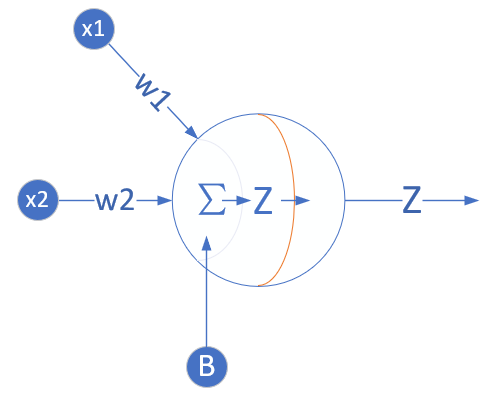
输入层
单独看第一个样本是这样的：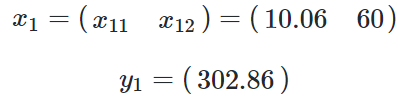
一共有1000个样本，每个样本2个特征值，X就是一个1000×2的矩阵：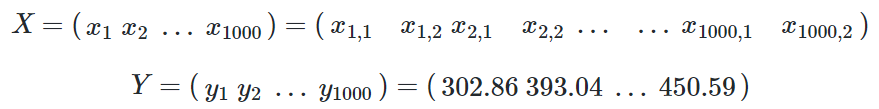
x1 表示第一个样本，x1,1表示第一个样本的一个特征值，y1是第一个样本的标签值。
权重W和B
由于我们只想完成一个回归（拟合）任务，所以输出层只有一个神经元。由于是线性的，所以没有用激活函数。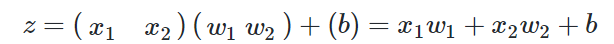
写成矩阵形式：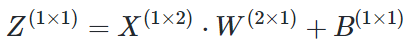
上述公式中括号中的数字表示该矩阵的（行x列）数。
对于拟合，可以想象成用一支笔在一堆点中画一条直线或者曲线，而那一个神经元就是这支笔。如果有多个神经元，可以画出多条线来，就不是拟合了，而是分类。
损失函数
因为是线性回归问题，所以损失函数使用均方差函数。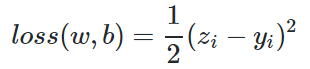
其中，zi是样本预测值，yi是样本的标签值。
反向传播
单样本多特征计算
与上一章不同，本章中的前向计算是多特征值的公式：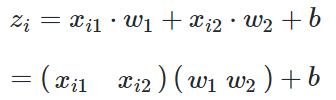
因为x有两个特征值，对应的W也有两个权重值。xi1表示第i个样本的第1个特征值，所以无论是x还是w都是一个向量或者矩阵了，那么我们在反向传播方法中的梯度计算公式还有效吗？答案是肯定的，我们来一起做个简单推导。
由于W被分成了w1和w2两部分，根据公式1和公式2，我们单独对它们求导：
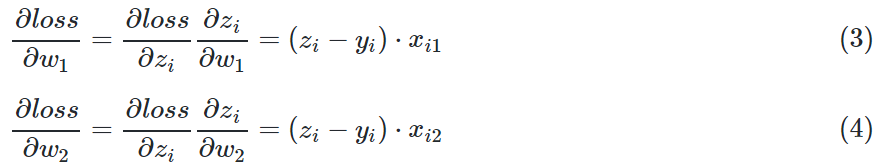
求损失函数对W矩阵的偏导，是无法求的，所以要变成求各个W的分量的偏导。由于W的形状是：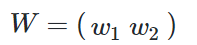
所以求loss对W的偏导，由于W是个矩阵，所以应该这样写：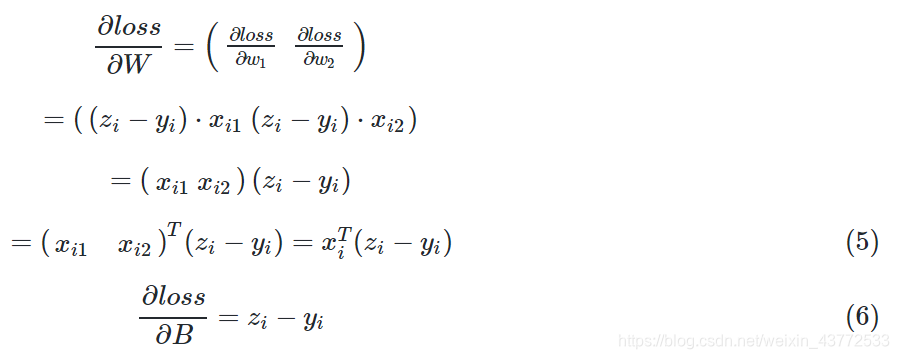
多样本多特征计算
当进行多样本计算时，我们用m=3个样本做一个实例化推导：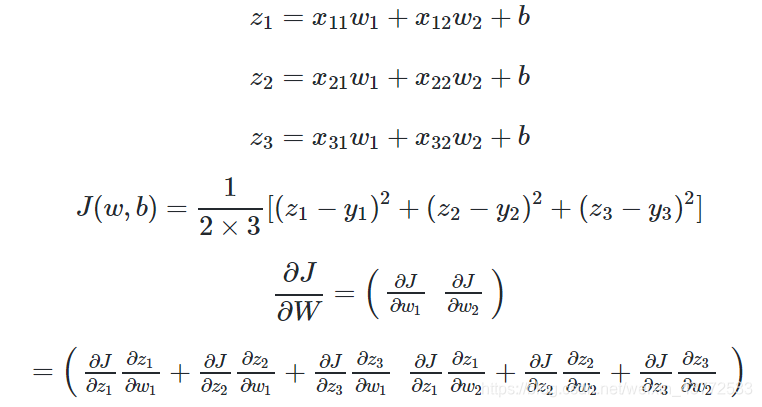
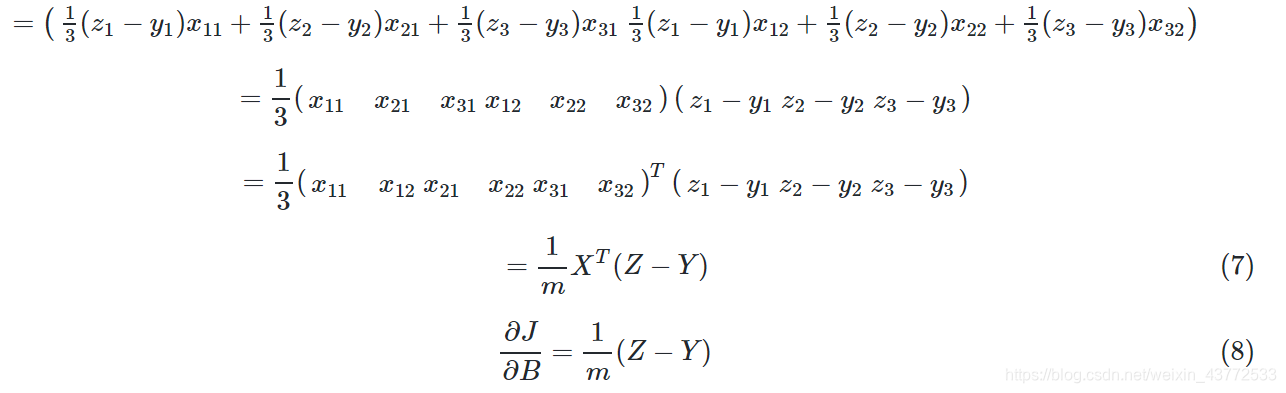
在这篇文章中，我们将拟合神经网络，并将线性模型作为比较。
数据集
数据集是郊区房屋价格数据的集合。我们的目标是使用所有其他可用的连续变量来预测自住房屋（medv）的中位数。
首先，我们需要检查是否缺少数据点，否则我们需要填充数据集。
apply（data，2，function（x）sum（is.na（x）））
然后我们拟合线性回归模型并在测试集上进行测试。
index < - sample（1：nrow（data），round（0.75 * nrow（data）））
MSE.lm < - sum（（pr.lm - test $ medv）^ 2）/ nrow（test）
sample(x,size)函数简单地从向量输出指定大小的随机选择样本的向量x。
准备拟合神经网络
在拟合神经网络之前，需要做一些准备工作。神经网络不容易训练和调整。
作为第一步，我们将解决数据预处理问题。
因此，我们先划分数据：
maxs < - apply（data，2，max）
scaled < - as.data.frame（scale（data，center = mins，scale = maxs - mins））
train_ < - scaled [index，]
test_ < - scaled [-index，]
请注意，scale需要转换为data.frame的矩阵。
参数
虽然有几个或多或少可接受的经验法则，但没有固定的规则可以使用多少层和神经元。一般一个隐藏层足以满足大量应用程序的需要。就神经元的数量而言，它应该在输入层大小和输出层大小之间，通常是输入大小的2/3
hidden参数接受一个包含每个隐藏层的神经元数量的向量，而参数linear.output用于指定我们要进行回归linear.output=TRUE或分类linear.output=FALSE
绘制模型：
plot（nn）这是模型的图形表示，每个连接都有权重：
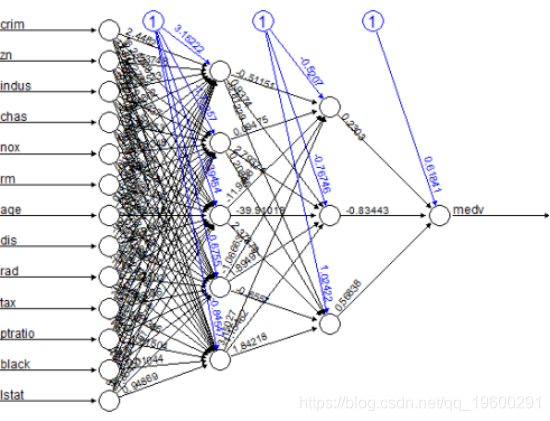
黑色线条显示每个层与每个连接上的权重之间的连接，而蓝线显示每个步骤中添加的偏差项。偏差可以被认为是线性模型的截距。
使用神经网络预测medv
现在我们可以尝试预测测试集的值并计算MSE。
pr.nn < - compute（nn，test _ [，1：13]）
然后我们比较两个MSE。
显然，在预测medv时，网络比线性模型做得更好。但是，这个结果取决于上面执行的训练测试集划分。下面，我们将进行快速交叉验证。
下面绘制了测试集上神经网络和线性模型性能的可视化结果
输出图：
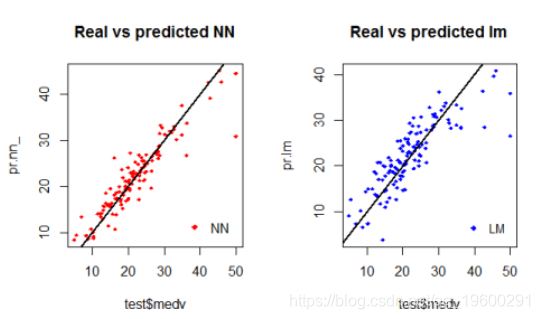
通过检查图，我们可以看到神经网络的预测（通常）在直线周围更加集中（与线完美对齐将表明MSE为0，因此是理想的完美预测）。
下面绘制了模型比较：
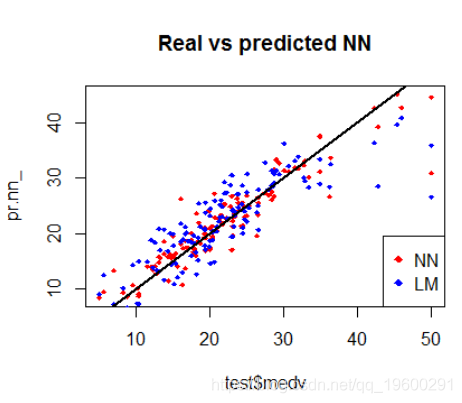
交叉验证
交叉验证是构建预测模型的另一个非常重要的步骤。有不同类型的交叉验证方法。
然后通过计算平均误差，我们可以掌握模型。
随时关注您喜欢的主题
我们将使用神经网络的for循环和线性模型cv.glm()的boot包中的函数来实现快速交叉验证。
据我所知，R中没有内置函数在这种神经网络上进行交叉验证。以下是线性模型的10折交叉验证MSE：
lm.fit < - glm（medv~。，data = data）
我以这种方式划分数据：90％的训练集和10％的测试集，随机方式进行10次。我使用plyr库初始化进度条，因为神经网络的拟合可能需要一段时间。
过了一会儿，过程完成，我们计算平均MSE并将结果绘制成箱线图:
cv.error
10.32697995
17.640652805 6.310575067 15.769518577 5.730130820 10.520947119 6.121160840
6.389967211 8.004786424 17.369282494 9.412778105
上面的代码输出以下boxplot：
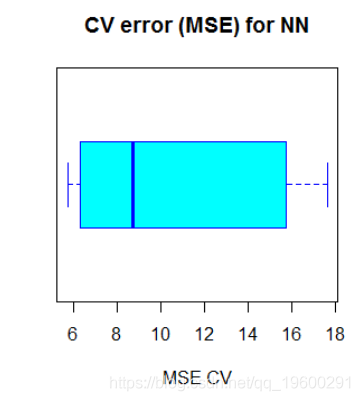
神经网络的平均MSE（10.33）低于线性模型的MSE，尽管交叉验证的MSE似乎存在一定程度的变化。这可能取决于数据的划分或网络中权重的随机初始化。
模型可解释性的说明
神经网络很像黑盒子：解释它们的结果要比解释简单模型（如线性模型）的结果要困难得多。因此，根据您需要解决的应用问题的类型，也要考虑这个因素。此外，需要小心拟合神经网络，小的变化可能导致不同的结果。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】Python深度神经网络DNNs-K-Means（K-均值）聚类方法在MNIST等数据可视化对比分析
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
