最近我们被客户要求撰写关于Nelson-Siegel模型的研究报告。Nelson-Siegel- [Svensson]模型是拟合收益曲线的常用方法。

由Kaizong Ye，Coin Ge撰写

它的优点是其参数的经济可解释性，被银行广泛使用。但它不一定在所有情况下都有效：模型参数有时非常不稳定，无法收敛。

纳尔逊（Nelson）和西格尔（Siegel）在其原始论文中从远期利率入手，然后推导了收益率至到期曲线的公式.

可下载资源

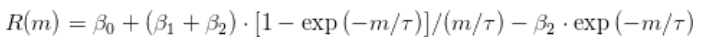
Nelson-Siegel模型是简约的，可以生成丰富的收益曲线。

但是，由于简单地使用它，它通常失去了经济上的可解释性，甚至无法收敛。

发现有效的、合理的利率期限机构一直是中国金融学界学者孜孜以求的研究课题。中国利率期限结构曲线的研究始于 20 世纪 90 年代中后期，以国债和同业拆借利率为样本，用即期利率模型和动态利率模型研究利率期限结构，例如范龙振构建了上海证券交易所债券价格隐含的利率期限结构的连续时间两因子 Vasicek 利率模型[1]；朱世武和陈健恒运用多项式样条法和 Nelson－Siegel 模型对我国交易所国债利率期限结构进行了实证研究[2]；谢赤和吴雄伟基于国内市场数据对具有状态变量的 HJM 模型、Vasicek 和 CIR 模型进行了实证分析[3] ；郑振龙/林海利用 McCulloch 样条函数和息票剥离法对我国市场利率期限结构进行了静态估计，构造出中国真正的市场利率期限结构[4]。这些研究成果尽管取得了一定的成绩，但这些研究几乎都是用国外已有的模型直接运用到国内的原始交易数据，存在以下的不足之处：首先，大部分以交易所国债价格为样本的研究，并没有考虑到交易所国债品种少、交易不活跃的事实；其次，以银行间国债价格为样本的研究，虽然包含了较多的国债样本，但是并没有考虑到哪些样本点是真实有效的交易；第三，以银行间拆借市场利率为样本的短期利率建模研究并没有考虑到同业拆借采取的是寻价机制，样本点并不能反映实际的成交价格；最后，这些研究的主要目的是探询并解释中国基准利率期限的形状和特征，并没有讨论在需要用每日样本更新模型参数的情况下，模型的有效性。

[1]. 范龙振. 上交所债券利率期限结构与两因子 Vasicek 模型[J].复旦学报: 自然科学版, 2003, 42(005): 773-778.

[2]. 朱世武、陈健恒, 交易所国债利率期限结构实证研究[J]. 金融研究, 2003 10: 63-73.

[3] 谢赤, 吴雄伟. 基于 Vasicek 和 CIR 模型中的中国货币市场利率行为实证分析[J].中国管理科学, 2002, 10:22-25.

[4] 郑振龙,林海.中国市场利率期限结构的静态估计[J].武汉金融, 2003,3: 33-36.

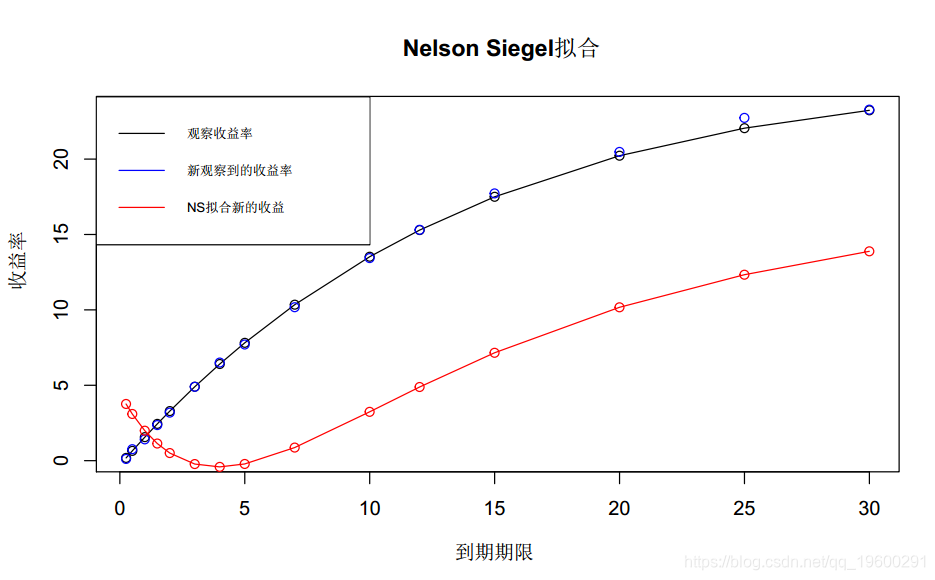
上图显示了这种情况。

 plot(MATURITY_BASES, oldYields
lines(MATURITY_BASES, oldYields)
points(newMats, newYields, col="blue")
lines(newMats, newYields, col="blue")

此代码模仿了一个频繁使用的案例，当前的收益曲线与昨天的曲线进行了比较。

从某种意义上讲，这是一个简单示例，因为对于给定的到期日，我们已经具有零收益率。实际上，我们通常与票息债券有关，这会使事情变得更加复杂。

您可能会认为，由于软件的实施而导致收敛失败。我要讲的不是不好的实现，而是要高度依赖所使用的数值方法，如下面的更实际的示例所示。

提供更逼真的建模

#include <ql/qldefines.hpp>
#ifdef BOOST_MSVC
#  include <ql/auto_link.hpp>
#endif
#include <ql/termstructures/yield/fittedbonddiscountcurve.hpp>
#include <ql/termstructures/yield/piecewiseyieldcurve.hpp>
#include <ql/termstructures/yield/flatforward.hpp>
#include <ql/termstructures/yield/bondhelpers.hpp>
#include <ql/termstructures/yield/nonlinearfittingmethods.hpp>

 
using namespace QuantLib;
 
int main(int, char*[]) {
    try {
        Calendar calendar = NullCalendar();
        Date today = Date(18, December, 2017);
        Settings::instance().evaluationDate() = today;
 
        //市场数据
        double cleanPrices1[] = { 107.96, 135.88, 110.6,   133.46, 135.8,  142.155, 121.045, 134.97, 117.04,
            101.61, 128.67, 106.615, 106.36, 99.515, 101.21,  105.655, 114.828 };
        double cleanPrices2[] = { 107.9,  134.965, 110.37,  132.89, 135.62,140.845, 120.585, 133.995, 116.745,
            101.58, 128.115,105.985, 105.395,99.385, 100.79,104.955, 114.7985 };
        double cleanPrices3[] = { 107.96, 134.625, 110.58, 132.65, 135.145, 140.585, 120.385, 133.735, 116.635,
            101.62, 127.925, 105.6, 105.085, 99.29, 100.6, 104.945, 114.7415 };
        double cleanPrices4[] = { 107.78, 134.39, 110.175, 132.445, 134.905, 139.515, 120.115, 133.475, 116.455,
            101.58, 127.845, 105.53,104.805, 99.07, 100.46, 104.885, 114.6225 };

 
        std::vector<boost::shared_ptr<BondHelper> > bondHelpersA;
        std::vector< boost::shared_ptr<SimpleQuote> > quoteA;
        std::vector<boost::shared_ptr<BondHelper> > bondHelpersB;

        for (Size i = 0; i < numberOfBonds; i++) {
            boost::shared_ptr<SimpleQuote> cp1(new SimpleQuote(cleanPrices1<em class="d4pbbc-italic"></em>));
            quoteA.push_back(cp1);
            boost::shared_ptr<SimpleQuote> cp2(new SimpleQuote(cleanPrices2<em class="d4pbbc-italic"></em>));
            quoteB.push_back(cp2);
            boost::shared_ptr<SimpleQuote> cp3(new SimpleQuote(cleanPrices3<em class="d4pbbc-italic"></em>));
            quoteC.push_back(cp3);
            boost::shared_ptr<SimpleQuote> cp4(new SimpleQuote(cleanPrices4<em class="d4pbbc-italic"></em>));
            quoteD.push_back(cp4);
        }
 
        RelinkableHandle<Quote> quoteHandleA[numberOfBonds];

最受欢迎的见解

1.在python中使用lstm和pytorch进行时间序列预测

2.python中利用长短期记忆模型lstm进行时间序列预测分析

3.Python用RNN循环神经网络：LSTM长期记忆、GRU门循环单元、回归和ARIMA对COVID-19新冠疫情新增人数时间序列

4.Python TensorFlow循环神经网络RNN-LSTM神经网络预测股票市场价格时间序列和MSE评估准确性

5.r语言copulas和金融时间序列案例

6.R 语言用RNN循环神经网络、LSTM长短期记忆网络实现时间序列长期利率预测

7.Matlab创建向量自回归（VAR）模型分析消费者价格指数 (CPI) 和失业率时间序列

8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类

9.R语言结合新冠疫情COVID-19股票价格预测：ARIMA，KNN和神经网络时间序列分析

        //Nelson-Siegel模型拟合
        Real tolerance = 1.0e-14;
        Size max = 10000;
 
        boost::shared_ptr<FittedBondDiscountCurve> tsA(
            new FittedBondDiscountCurve(curveSettlementDays,
                calendar,
                instrumentsA,
                ActualActual(),
                NelsonSiegelFitting(),
                tolerance,
                max));
 
 
        boost::shared_ptr<FittedBondDiscountCurve> tsB(
            new FittedBondDiscountCurve(curveSettlementDays,
                calendar,
                instrumentsB,
                ActualActual(),
                NelsonSiegelFitting(),
                tolerance,
                max));
 
        boost::shared_ptr<FittedBondDiscountCurve> tsC(
            new FittedBondDiscountCurve(curveSettlementDays,
                calendar,
                instrumentsC,
                ActualActual(),
                NelsonSiegelFitting(),
                tolerance,
                max));
 
        boost::shared_ptr<FittedBondDiscountCurve> tsD(
            new FittedBondDiscountCurve(curveSettlementDays,
                calendar,
                instrumentsD,
                ActualActual(),
                NelsonSiegelFitting(),
                tolerance,
                max));
 
        std::cout << tsA->fitResults().numberOfIterations() << std::endl;
        std::cout << tsB->fitResults().numberOfIterations() << std::endl;

正式而言，收益曲线每天的变化并不显着，但是模型参数却可以：

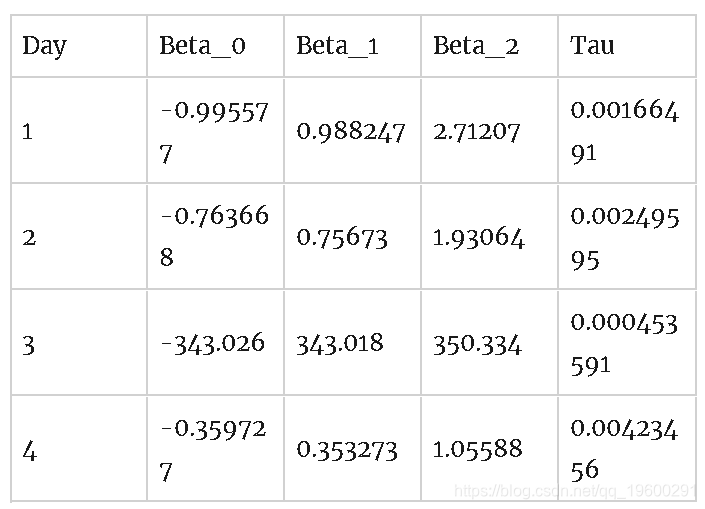
R语言用神经网络改进Nelson-Siegel模型拟合收益率曲线分析

阅读文章 ➜

Nelson-Siegel意识到了这些问题，并提供了解决这些问题的方法。特别是，他们考虑了Taus的时间序列，并确定了Taus的最佳拟合值的中值和合理范围。
但是，与往常一样，原始论文被引用的次数可能多于阅读次数。此外，如果需要按时间顺序排列的收益率数据，可能会感到困惑，而不是仅仅考虑相关日期的数据。即使处理时间序列不是问题，Nelson和Siegel也没有指定_正式的_算法来选择的最佳值。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！