R语言向量自回归模型(VAR)及其实现

澳大利亚在2008 – 2009年全球金融危机期间发生了这种情况。澳大利亚政府发布了一揽子刺激计划

由Kaizong Ye，Sherry Deng撰写

其中包括2008年12月的现金支付，恰逢圣诞节。 因此，零售商报告销售强劲，经济受到刺激。因此，收入增加了。

可下载资源

完整程序、数据和文档（word）

VAR面临的批评是他们是理论上的; 也就是说，它们不是建立在一些经济学理论的基础上，这些理论强加了方程式的理论结构。假设每个变量都影响系统中的其他变量，这使得估计系数的直接解释变得困难。尽管如此，VAR在几种情况下都很有用：

向量自回归模型的英文名称为Vector Autoregressive model，常被简写成VAR。向量自回归的出现由来已久，可以追溯到上个世纪80年代，人们构建向量自回归模型主要出于以下考虑：

时间序列分析从单一时间序列 (time series data) 拓展到了多元时间序列 (multivariate time series)，在任意第 ${\color{blue}{t}}$ 个时间间隔 (time interval)，观测样本从 ${\color{blue}{1}}$ 变成了 ${\color{blue}{N}}$ ，其中， ${\color{blue}{N}}$ 表示多元时间序列中时间序列的数量。
标准的自回归模型 (Autoregressive model, 简称AR) 其表达式过于简单，无法很好地在多元时间序列分析中发挥作用。

1 标准的自回归模型

在统计学、经济学乃至信号处理等领域，自回归模型被广泛应用于描述随时间变化的过程 (简称时变过程)，其中，最为经典的应用当属时间序列分析，在这里，自回归模型假设变量之间存在一个线性的依赖关系，即输出变量 (output variables) 如 ${\color{blue}{y_t}}$ 与输入的历史变量 (previous variables) 如 ${\color{blue}{y_{t-1},y_{t-2},...}}$ 存在一个线性表达式。

不妨先看一下标准的自回归模型：给定单一时间序列 ${\color{blue}{\boldsymbol{y}\in\mathbb{R}^{T}}}$ ，其时间间隔的数量为 ${\color{blue}{T}}$ ，则对于任意第 ${\color{blue}{t}}$ 个时间间隔，存在如下的线性表达式：

${\color{blue}{y_{t}=\sum_{k=1}^{d}a_ky_{t-k}+\epsilon_t,~t=d+1,...,T,}}$

其中， ${\color{blue}{a_k,k=1,2,...,d}}$ 表示回归系数；常数 ${\color{blue}{d}}$ 表示自回归模型的阶数 (order)，也可以将 ${\color{blue}{d}}$ 简单地理解成当前时间点关联过去时间点的数量。

在自回归模型中，我们的目标是从观测数据中学习出参数 ${\color{blue}{a_k,k=1,...,d}}$ 。现假设观测数据为 ${\color{blue}{\boldsymbol{y}\in\mathbb{R}^{T}}}$ ，首先，我们需要对自回归模型的线性表达式进行改写：

${\color{blue}{\begin{aligned} &y_{t}\approx\boldsymbol{a}^\top{\boldsymbol{v}}_{t},~t=d+1,...,T, \\ \Rightarrow&\boldsymbol{z}\approx Q\boldsymbol{a}, \end{aligned}}}$

其中， ${\color{blue}{{\boldsymbol{v}}_{t}=\left(y_{t-1},y_{t-2},...,y_{t-d}\right)\in\mathbb{R}^{d}}}$ ； ${\color{blue}{\boldsymbol{z}=\left(y_{d+1},y_{d+2},...,y_{T}\right)\in\mathbb{R}^{T-d}}}$ ； ${\color{blue}{Q=\left[\begin{array}{c}{\boldsymbol{v}_{d+1}^{\top}} \\ {\vdots} \\ {\boldsymbol{v}_{T}^{\top}}\end{array}\right] \in \mathbb{R}^{(T-d) \times d}}}$ . 在这里，写成这种形式完全是为了简化后续的推导。

如果进一步将 ${\color{blue}{\epsilon_t}}$ 作为高斯噪声，采用最小二乘法，则回归系数 ${\color{blue}{\boldsymbol{a}}}$ 的最优解为

${\color{blue}{\begin{aligned} \boldsymbol{a}&=\text{arg}\min_{\boldsymbol{x}}~\frac{1}{2}\sum_{t=d+1}^{T}\left(y_{t}-\boldsymbol{x}^\top{\boldsymbol{v}}_{t}\right)^2 \\ &=\text{arg}\min_{\boldsymbol{x}}~\frac{1}{2}\left(\boldsymbol{z}-Q\boldsymbol{x}\right)^\top\left(\boldsymbol{z}-Q\boldsymbol{x}\right) \\ &=\text{arg}\min_{\boldsymbol{x}}~\frac{1}{2}\left(\boldsymbol{x}^\top Q^\top Q\boldsymbol{x}-\boldsymbol{z}^\top Q\boldsymbol{x}-\boldsymbol{x}^\top Q^\top\boldsymbol{z}\right) \\ &=\left(Q^\top Q\right)^{-1}Q^\top\boldsymbol{z}. \\ \end{aligned}}}$

2 多元时间序列

实际上，相比单一的时间序列数据，多元时间序列数据反而更为常见，是由单一的时间序列构成，如下面的矩阵

${\color{blue}{Y=\left[\begin{array}{ccccc} y_{11} & \cdots & y_{1t} & \cdots & y_{1T} \\ y_{21} & \cdots & y_{2t} & \cdots & y_{2T} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ y_{N1} & \cdots & y_{Nt} & \cdots & y_{NT} \\ \end{array} \right]\in\mathbb{R}^{N\times T}}}$

就是一般形式的多元时间序列数据。在矩阵 ${\color{blue}{Y}}$ 中，任意第 ${\color{blue}{t}}$ 个时间间隔下，观测值为

${\color{blue}{\boldsymbol{y}_{t}=\left(y_{1t},y_{2t},...,y_{Nt}\right)^\top\in\mathbb{R}^{N}, }}$

观测值的数量为 ${\color{blue}{N}}$ .

3 向量自回归模型

针对多元时间序列数据，向量自回归模型采用了一种更为灵活的时序建模策略：给定多元时间序列数据为 ${\color{blue}{Y\in\mathbb{R}^{N\times T}}}$ ，则对于任意第 ${\color{blue}{t}}$ 个时间间隔，存在如下的线性表达式：

${\color{blue}{\boldsymbol{y}_{t}=\sum_{k=1}^{d}A_k\boldsymbol{y}_{t-k}+\boldsymbol{\epsilon}_{t},~t=d+1,...,T,}}$

其中， ${\color{blue}{A_k\in\mathbb{R}^{N\times N},k=1,2,...,d}}$ 表示向量自回归模型的系数矩阵； ${\color{blue}{\boldsymbol{\epsilon}_t}}$ 可视为高斯噪声。

为方便后续推导，与自回归模型类似，令

${\color{blue}{A=\left[A_{1}, \ldots, A_{d}\right]^{\top} \in \mathbb{R}^{(N d) \times N}, \quad \boldsymbol{v}_{t}=\left[\begin{array}{c}{\boldsymbol{y}_{t-{1}}} \\ {\vdots} \\ {\boldsymbol{y}_{t-{d}}}\end{array}\right] \in \mathbb{R}^{(N d)},}}$

将向量自回归模型进行改写：

${\color{blue}{\begin{aligned} \boldsymbol{y}_{t}&\approx \sum_{k=1}^{d}A_k\boldsymbol{y}_{t-k}, \\ &=A^\top\boldsymbol{v}_{t},~t=d+1,...,T, \\ \Rightarrow Z&\approx QA, \\ \end{aligned}}}$

其中，公式中的矩阵 ${\color{blue}{Z}}$ 和 ${\color{blue}{Q}}$ 定义如下：

${\color{blue}{Z=\left[\begin{array}{c}{\boldsymbol{y}_{{d}+1}^{\top}} \\ {\vdots} \\ {\boldsymbol{y}_{T}^{\top}}\end{array}\right] \in \mathbb{R}^{\left(T-{d}\right) \times N}, \quad Q=\left[\begin{array}{c}{\boldsymbol{v}_{{d}+1}^{\top}} \\ {\vdots} \\ {\boldsymbol{v}_{T}^{\top}}\end{array}\right] \in \mathbb{R}^{(T-d) \times(N d)}.}}$

由此，采用最小二乘法，系数矩阵 ${\color{blue}{A}}$ 的最优解为

${\color{blue}{\begin{aligned} A&=\text{arg}\min_{X}~\frac{1}{2}\left\|Z-QX\right\|_{F}^{2} \\ &=\text{arg}\min_{X}~\frac{1}{2}\text{tr}\left(\left(Z-QX\right)^\top\left(Z-QX\right)\right) \\ &=\text{arg}\min_{X}~\frac{1}{2}\text{tr}\left(X^\top Q^\top QX-Z^\top QX-X^\top Q^\top Z\right) \\ &=\left(Q^\top Q\right)^{-1}Q^\top Z. \\ \end{aligned}}}$

在这里，我们用到了F-范数与矩阵迹 (trace) 之间的等价变换，它的意义是为了方便推导，如何简单理解这种等价变换呢？举一个例子：给定任意大小为 $2\times 2$ 的矩阵
$A=\left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right]\in\mathbb{R}^{2\times 2},$
由于F-范数是矩阵所有元素的平方和开根号，即 $\|A\|_{F}=\left(a_{11}^{2}+a_{12}^{2}+a_{21}^{2}+a_{22}^{2}\right)^{\frac{1}{2}},$
另外，
$A^\top A=\left[\begin{array}{cc} a_{11}^2+a_{21}^2 & a_{11}a_{12}+a_{21}a_{22} \\ a_{12}a_{11}+a_{22}a_{21} & a_{12}^{2}+a_{22}^{2} \\ \end{array}\right],$
因此，根据矩阵迹的定义，有
$\text{tr}\left(A^\top A\right)=a_{11}^{2}+a_{12}^{2}+a_{21}^{2}+a_{22}^{2}=\|A\|_{F}^2.$

预测相关变量的集合，不需要明确的解释;
测试一个变量是否有助于预测另一个变量（格兰杰因果关系检验的基础）;
脉冲响应分析，其中分析了一个变量对另一个变量的突然但暂时的变化的响应;
预测误差方差分解，其中每个变量的预测方差的比例归因于其他变量的影响。

示例：用于预测美国消费的VAR模型

Bilibili Video Embed

视频

向量自回归VAR数学原理及R语言软件经济数据脉冲响应分析实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

 
VARselect(uschange[,1:2], lag.max=8,
type="const")[["selection"]]
#> AIC(n) HQ(n) SC(n) FPE(n)
#> 5 1 1 5

R输出显示每个信息标准选择的滞后期。由AIC选择的VAR（5）与BIC选择的VAR（1）之间存在很大差异。因此，我们首先拟合由BIC选择的VAR（1）。

var1 <- VAR(uschange[,1:2], p=1, type="const")
serial.test(var1, lags.pt=10, type="PT.asymptotic")
var2 <- VAR(uschange[,1:2], p=2, type="const")
serial.test(var2, lags.pt=10, type="PT.asymptotic")

与单变量ARIMA方法类似，我们使用Portmanteau测试残差是不相关的。VAR（1）和VAR（2）都具有一些残差序列相关性，因此我们拟合VAR（3）。

var3 <- VAR(uschange[,1:2], p=3, type="const")
serial.test(var3, lags.pt=10, type="PT.asymptotic")
#>
#> Portmanteau Test (asymptotic)
#>
#> data: Residuals of VAR object var3
#> Chi-squared = 34, df = 28, p-value = 0.2

该模型的残差通过了序列相关性检验。VAR（3）生成的预测如图所示。

forecast(var3) %>%
autoplot() + xlab("Year")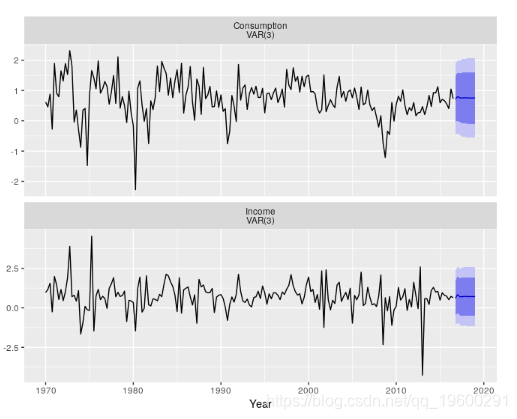

最受欢迎的见解

1.在python中使用lstm和pytorch进行时间序列预测

2.python中利用长短期记忆模型lstm进行时间序列预测分析

3.Python用RNN循环神经网络：LSTM长期记忆、GRU门循环单元、回归和ARIMA对COVID-19新冠疫情新增人数时间序列

4.Python TensorFlow循环神经网络RNN-LSTM神经网络预测股票市场价格时间序列和MSE评估准确性

5.r语言copulas和金融时间序列案例

6.R 语言用RNN循环神经网络、LSTM长短期记忆网络实现时间序列长期利率预测

7.Matlab创建向量自回归（VAR）模型分析消费者价格指数 (CPI) 和失业率时间序列

8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类

9.R语言结合新冠疫情COVID-19股票价格预测：ARIMA，KNN和神经网络时间序列分析

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言向量自回归模型(VAR)及其实现

1 标准的自回归模型

2 多元时间序列

3 向量自回归模型

示例：用于预测美国消费的VAR模型

相关文章

关注有关新文章的微信公众号