本文包含各种过滤器,可用于分解南非GDP的方法。
分解南非GDP数据
rm(list = ls())
graphics.off()
载入数据
如前所述,南非的GDP数据将其作为时间序列存储在gdp中,我们执行以下命令。
gdp <- ts(dat.tmp, start = c(1960, 2), frequency = 4)为了确保这些计算和提取的结果是正确的,我们检查一下数据的图表。
plot(gdp)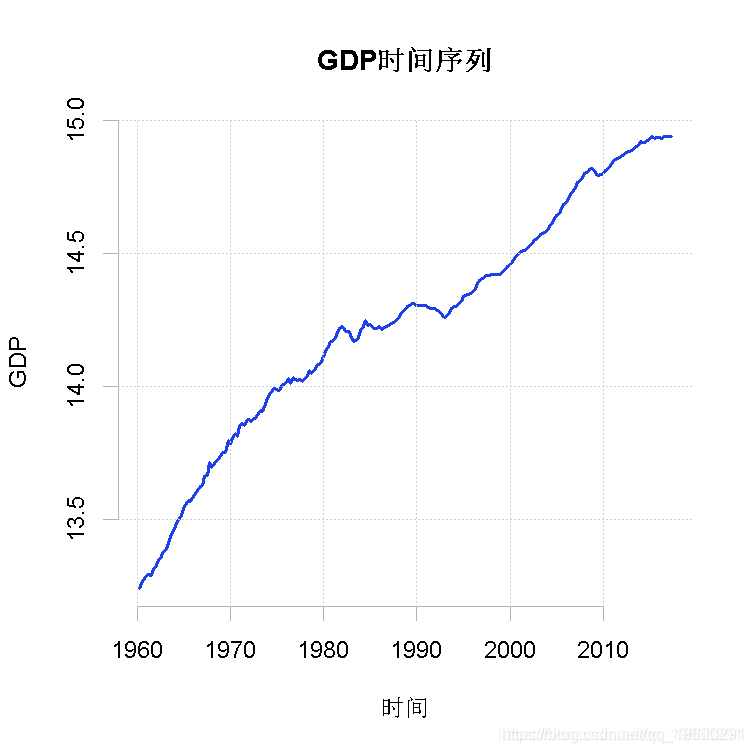
线性滤波器_去除数据线性趋势_
为了估计一个线性趋势,我们可以利用一个包括时间趋势和常数的线性回归模型。为了估计这样一个模型,我们使用lm命令,如下。
lin.mod$fitted.values # 拟合值与时间趋势有关
ts(lin.trend, start = c(1960, 1)) # 为趋势创建一个时间序列变量
gdp - linear # 周期是数据和线性趋势之间的差异回归的拟合值包含与线性趋势有关的信息。这些信息需要从模型对象lin.mod中提取,在上面的块中,我们将这些值分配给时间序列对象linear。然后从数据中剔除趋势,就得到了周期。
然后我们可以借助下面的命令来绘制这个结果,其中趋势和周期被绘制在不同的数字上。
plot.ts(gdp, ylab = "")
lines(linear, col = "red")
legend("topleft", legend = c("data", "trend")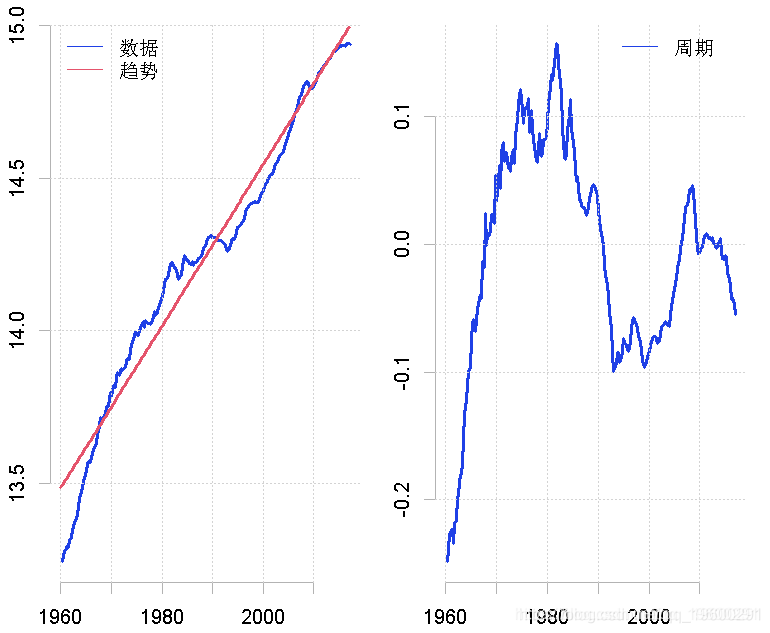
霍德里克 – 普雷斯科特 (Hodrick-Prescott,HP) _滤波器_对数据进行去趋势处理
要用流行的HP滤波法分解这个数据。在这种情况下,我们将lambda的值设置为1600,这也是对季度数据的建议。
hp(gdp, freq = 1600)
plot.ts(gdp, ylab = "") # 绘制时间序列
plot.ts(hp.decom$cycle, ylab = "") # 绘制周期图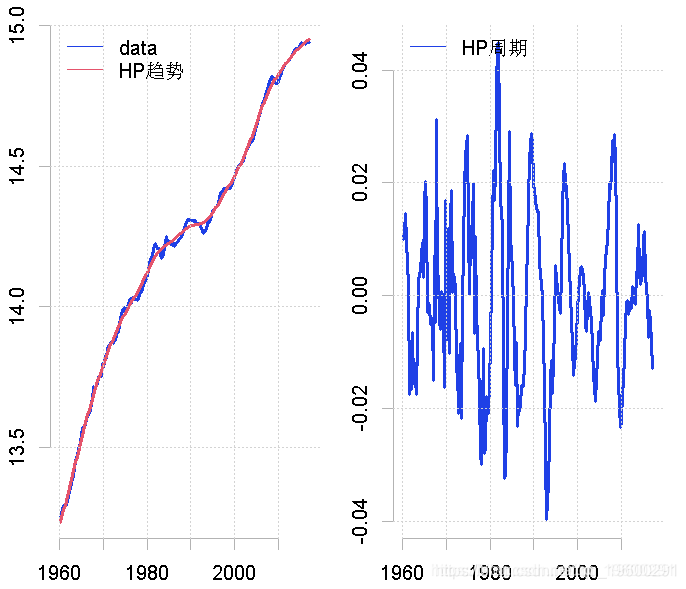
这似乎更准确地反映了我们对南非经济表现的理解。
用Baxter-King滤波器去趋势数据
为了利用Baxter-King 滤波器。在这种情况下,我们需要指定周期的频带,其上限被设定为32,下限被设定为6。
bk(gdp, pl = 6, pu = 32)
plot.ts(gdp, ylab = "")
plot.ts(cycle, ylab = "")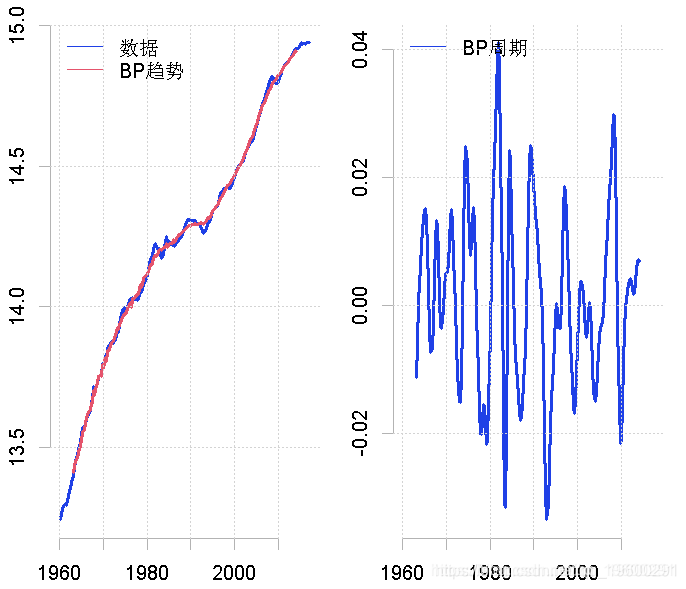
这似乎再次为南非经济活动的周期性提供了一个相当准确的表述。还要注意的是,周期的表示比以前提供的要平滑得多,因为噪音不包括在周期中。
Christiano-Fitzgerald滤波器去趋势数据
这个滤波器的性质与上面提供的非常相似。此外,产生与Baxter-King滤波器高度相似的结果。
plot.ts(gdp, ylab = "")
plot.ts(cfcycle, ylab = "")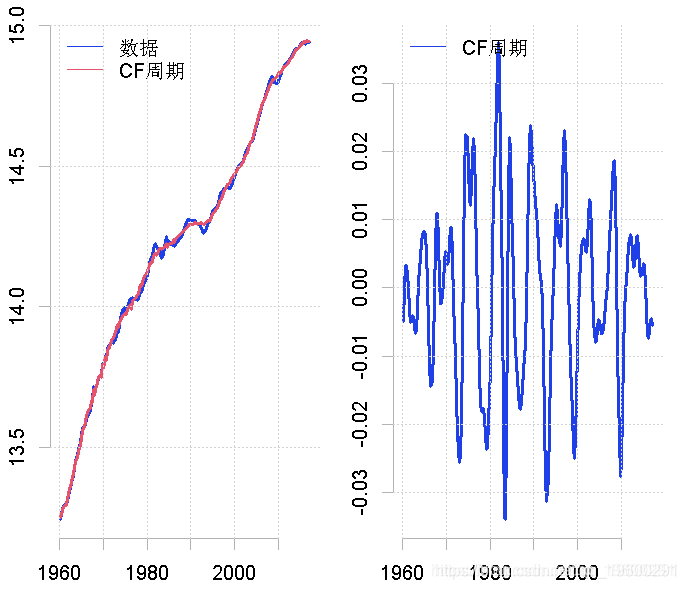
用Beveridge-Nelson分解法 “去趋势 “数据
为了将数据分解为随机趋势和平稳周期,我们可以采用Beveridge-Nelson分解法。当采用这种技术时,我们需要指定与平稳部分有关的滞后期的数量。在我下面的例子中,我假设有八个滞后期。
plot.ts(gdp, ylab = "")
lines(bn.trend, col = "red")
plot.ts(bn.cycle, ylab = "")比较周期的不同衡量标准
然后,我们可以将所有这些结果结合在一张图上,考虑各自的相似性和差异。在这个例子中,我创建了一个时间序列ts.union,但是我也可以先绘制一个单一的序列,然后再使用lines命令在上面绘制连续的图。
ts.union(lin.cycle, hp.decom, bp.decom,
cf.decom, bn.cycle)
plot.ts(comb, ylab = "")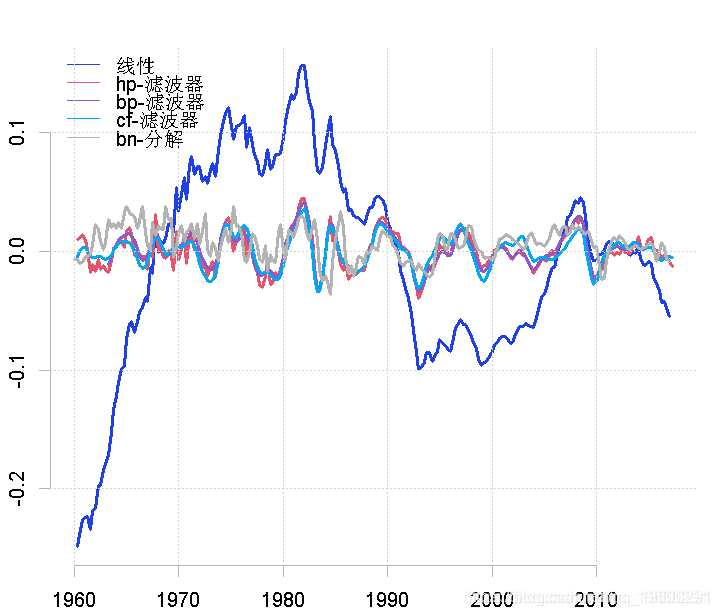
谱分解
在我们考虑使用谱技术之前,最好先清除当前环境中的所有变量,并关闭所有的图。下一步是确保你可以通过使用library命令来访问这些包中的程序。
随时关注您喜欢的主题
library(tsm)
library(TSA)
library(mFilter)使用谱技术进行分解。我们可以为三个时间序列变量生成数值,然后将它们组合成一个单一的变量。
2 * cos(2 * pi * t * w\[1\]) + 3 * sin(2 * pi * t *
w\[1\]) # no.obs点上的6个周期的频率
4 * cos(2 * pi * t * w\[2\]) + 5 * sin(2 * pi * t *
w\[2\]) #频率为10个周期的观察点
6 * cos(2 * pi * t * w\[3\]) + 7 * sin(2 * pi * t *
w\[3\]) # 在没有观测点的情况下,频率为40个周期
y <- x1 + x2 + x3为了观察这些变量,我们可以把它们绘制在一个单独的轴上。
par(mfrow = c(2, 2), mar = c(2.2, 2.2, 2, 1), cex = 0.8)
plot(x1, type = "l", main = "x1")
plot(x2, type = "l", main = "x2")
plot(x3, type = "l", main = "x3")
plot(y, type = "l", main = "y")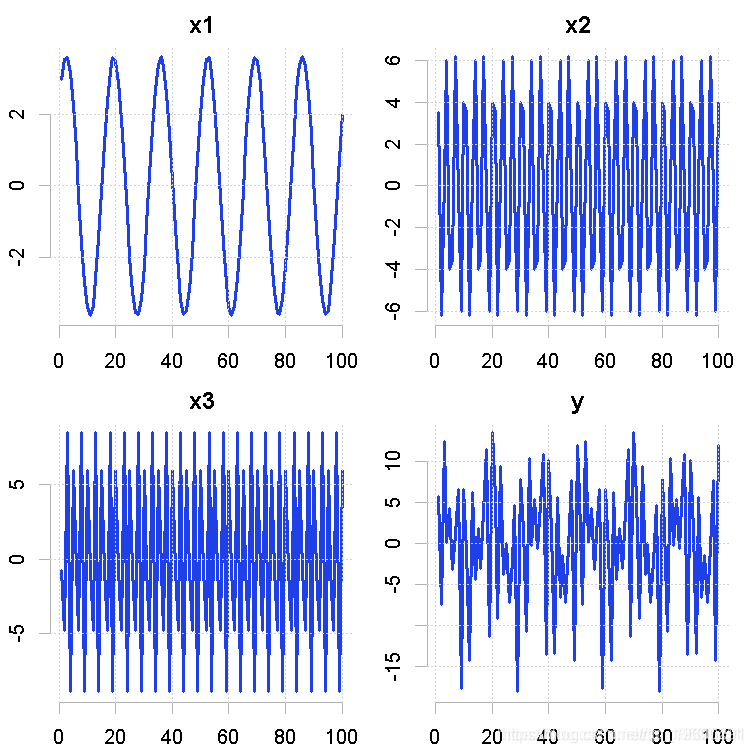
此后,我们可以使用周期图来考虑这些时间序列变量的每一个属性。
gram(y, main = "y", col = "red")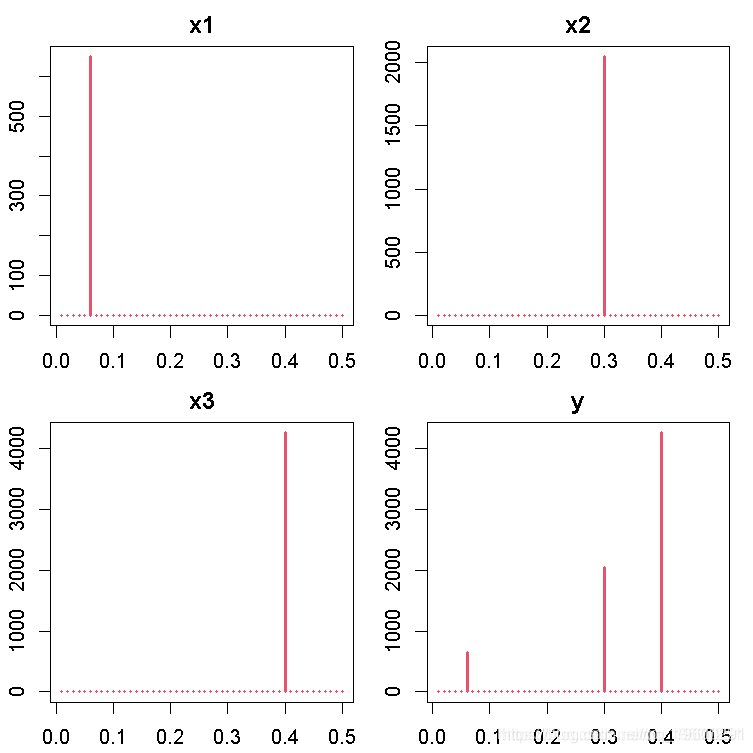
当然,我们可以利用一个过滤器,从总体时间序列变量中去除一些不需要的成分。为此,我们可以应用上下限相对较窄的Christiano-Fitzgerald滤波器。
此后,我们使用应用于与周期有关的信息的周期图,来调查它是否成功地剔除了一些频率成分。
cf(y0)
gram(cycle)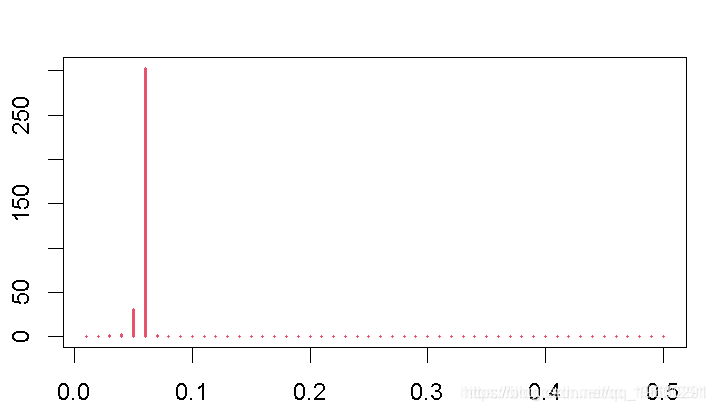
这个结果将表明,滤波器已经排除了大部分的高频率成分。为了看看这个周期与之前的数据有什么关系,我们把通过滤波器的周期性信息绘制在分量上。此外,我们还将这个结果绘制在综合周期的变量上。
plot(x1, type = "l", lty = 1)
lines(cycle, lty = 3, lwd = 3)
plot(y, type = "l", lty = 1)
lines(cycle, lty = 3, lwd = 3)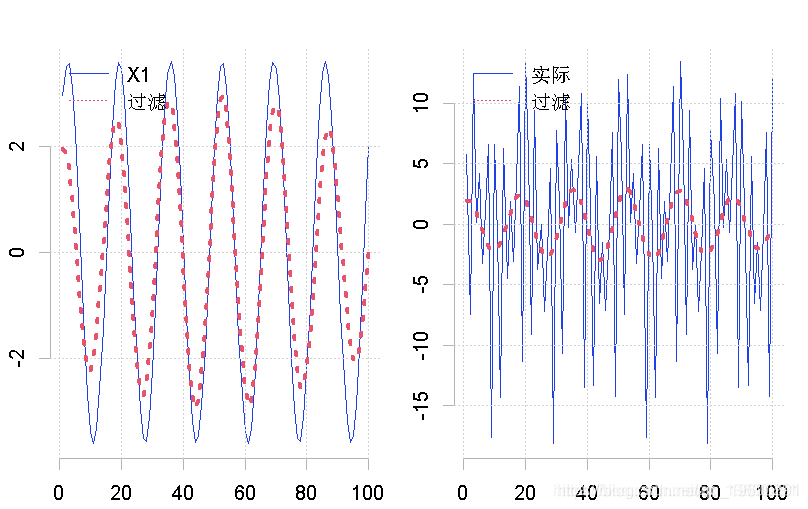
在这两种情况下,它似乎都对过程中的趋势做了合理的描述。
南非商业周期的谱分解法
为了考虑如何在实践中使用这些频谱分解,我们现在可以考虑将这些技术应用于南非商业周期的各种特征中。
下一步将是运行所有的过滤器,这些过滤器被应用于识别南非商业周期的不同方法。
现在,让我们对商业周期的每一个标准应用一个周期图。
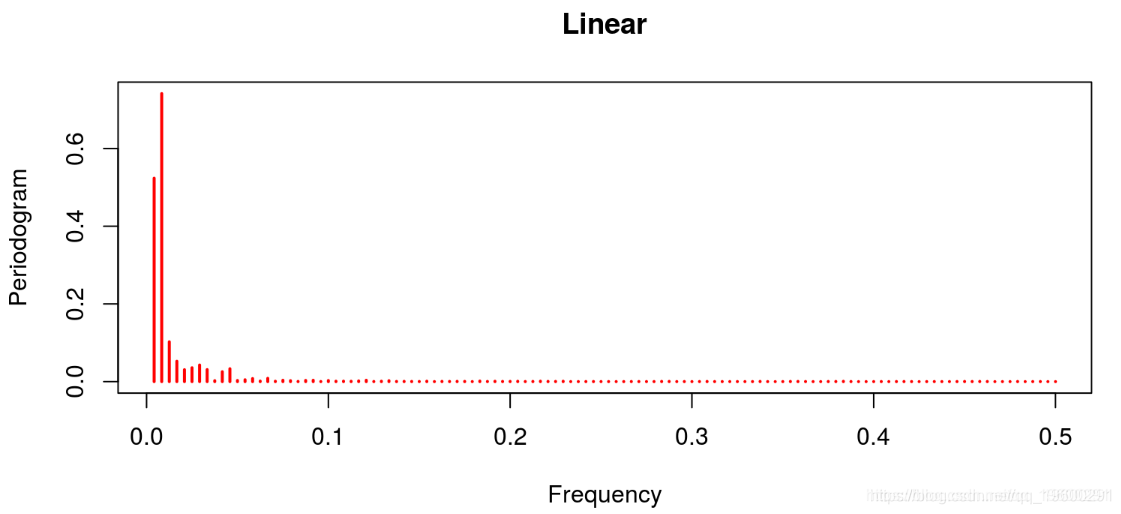
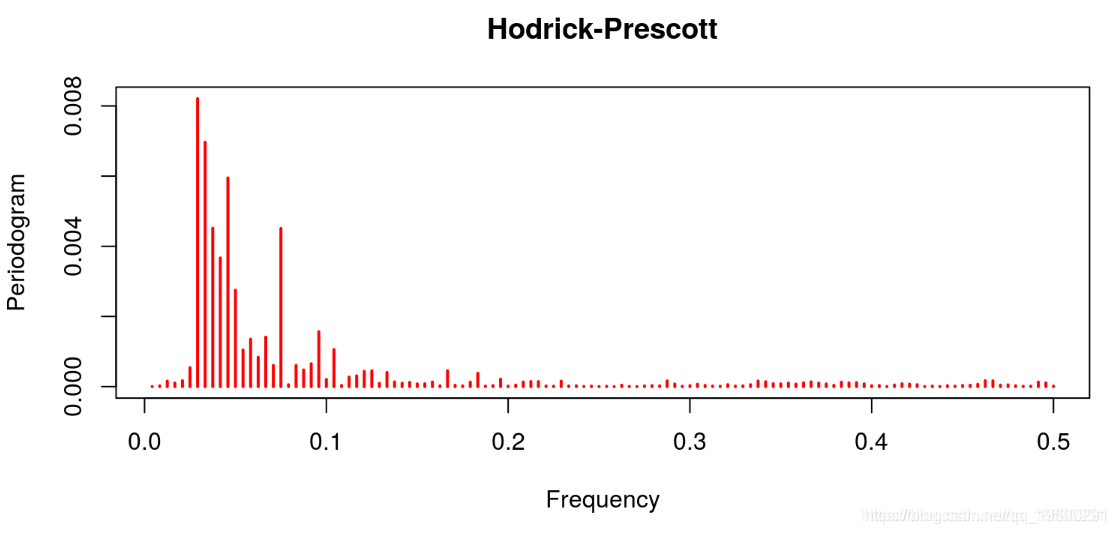
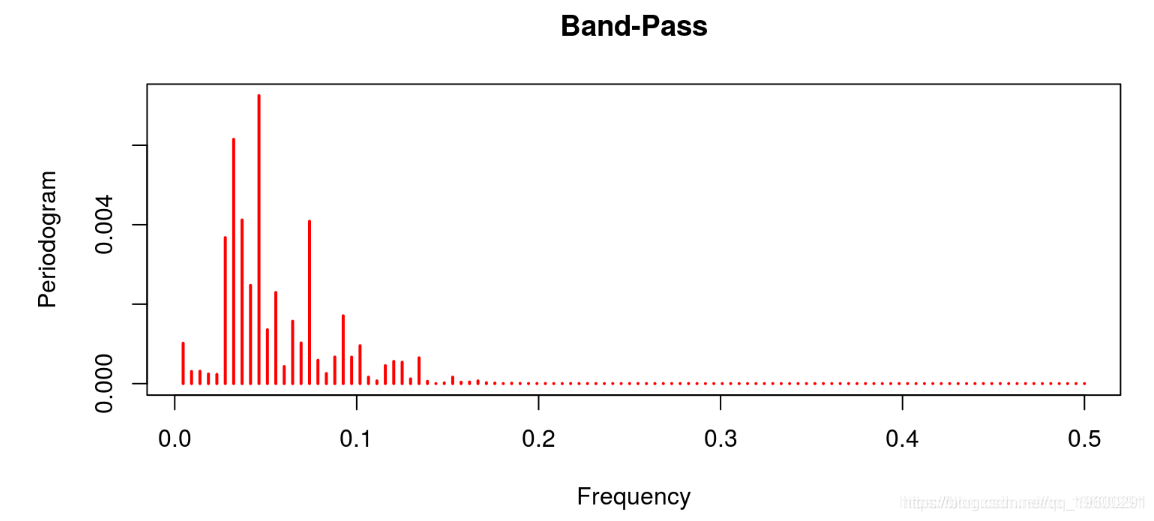
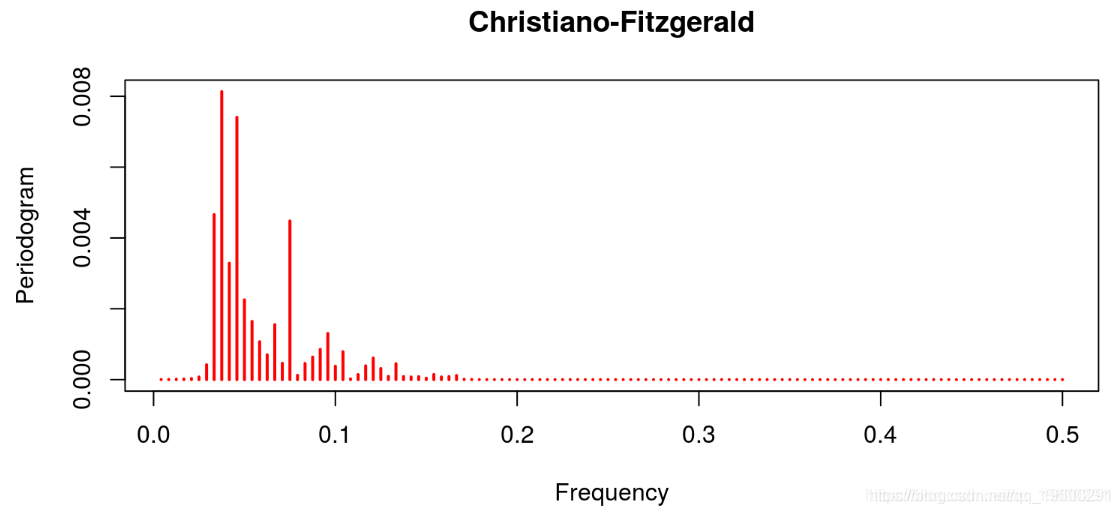
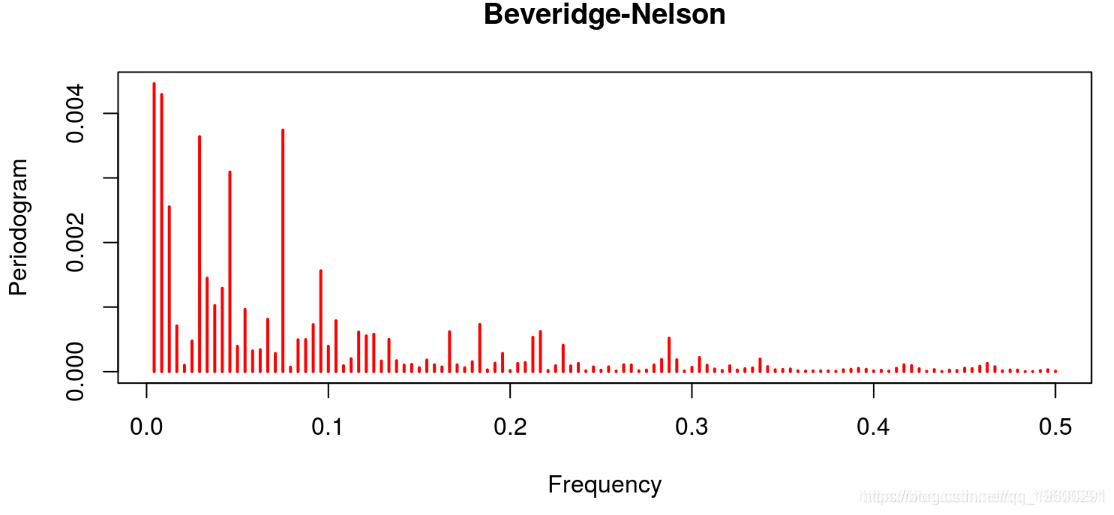
线性滤波器提供了一个很差的结果,因为趋势明显占主导地位(这不是周期应该有的)。这与Hodrick-Prescott滤波器的特征形成对比,后者的趋势信息已经被去除。Baxter & King和Christiano & Fitzgerald的带通滤波器也是这种情况。在这两种情况下,噪声也已经被去除。最后的结果与Beveridge-Nelson分解有关,我们注意到周期包括大量的趋势和大量的噪声。
小波分解
为了提供一个小波分解的例子,我们将把该方法应用于南非通货膨胀的数据。这将允许使用在这个过程中推导出对趋势的另一种衡量方法,这可以被认为是代表核心通货膨胀。请注意,这种技术可以应用于任何阶数的单整数据,所以我们不需要首先考虑变量的单整阶数。
然后,我们将利用消费者价格指数的月度数据,该数据包含在SARB的季度公告中。数据可以追溯到2002年。为了计算通货膨胀的同比指标,我们使用diff和lag命令。
diff/cpi\[-1 * (length - 11):length\]为了确保所有这些变量的转换都已正确进行,我们对数据进行绘图。
plot(inf.yoy)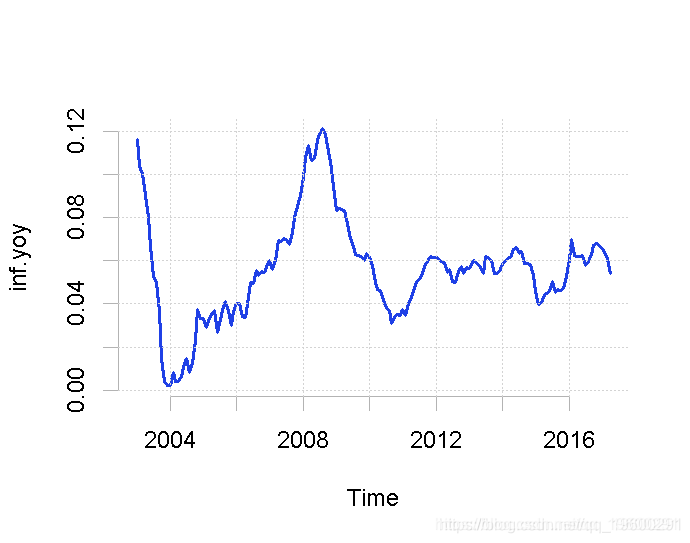
由于我们在这种情况下主要对识别平滑的趋势感兴趣,我们将使用贝希斯函数。这样的函数是Daubechies 4小波,它应用修正的离散小波变换方法。此外,我们还将使用三个母小波来处理各自的高频成分。
wt(yoy, "d4")然后我们可以为每个独立的频率成分绘制结果,如下所示。
plot.ts(yoy)
for (i in 1:4) plot.ts(d4\[\[i\]\]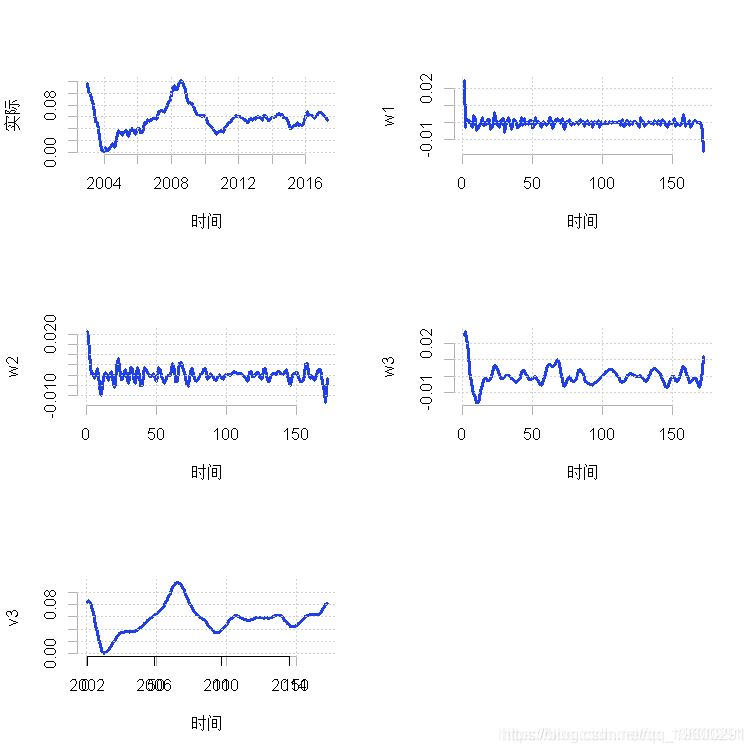
如果我们现在想在数据上绘制趋势(父小波)。
plot.ts(inf, ylab = "inf")
lines(ren)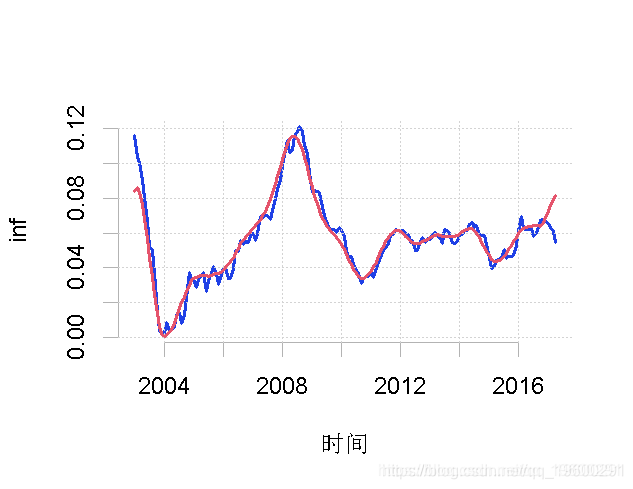
请注意,由于各自的频段是相加的,我们可以将其中一个母频段加入到趋势中,如下所示。
inf.tmp <- inf.tren + inf.d4$w3
inf.tren2 <- ts(inf.tmp, start = c(2003, 1), frequency = 12)
plot.ts(inf.yoy, ylab = "inf")
lines(inf.tren2, col = "red")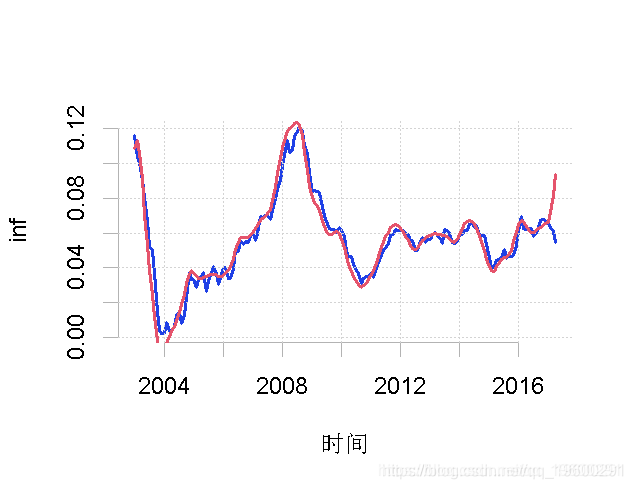
相关经济变量的周期性成分之间的相关性
为了确定周期的特征是否合适,我们可以考虑宏观经济总量的一些不同周期性方法之间的相关性。例如,我们可以考虑产出和生产(或就业)的周期性在不同的滞后期应该是相关的。如果它们不相关,那么该方法可能无法准确描述各自变量的周期性成分。
在本文使用的例子中,代码可能有点难以理解,但我们鼓励你自己去研究,以提高你对这个编码环境的总体理解。
下一步是读入数据并为数据的各种周期性成分创建一些矩阵。
yd <- dat\[5:n.obs, \] - dat\[1:(n.obs - 4), \] # 存储输出
yc_li <- matrix(rep(0, n.obs * n.var), ncol = n.var)
yc_hp <- matrix(rep(0, n.obs * n.var), ncol = n.var)
yc_bp <- matrix(rep(0, n.obs * n.var), ncol = n.var)
yc_bn <- matrix(rep(0, n.obs * n.var), ncol = n.var)使用上面包含的方法对数据进行过滤。
for (i in 1:n) {
# 用线性滤波器对数据进行去趋势处理
lin.mod <- lm(dat\[, i\] ~ time(dat\[, i\]))
# 用HP滤波器去趋势数据
yc_hp\[, i\] <- hp.cycle
#用带通滤波器去趋势数据
yc_bp\[, i\] <- bp.cycle
# Beveridge-Nelson分解
yc_bn\[, i\] <- bn.\[, 2\]
}计算不同提前期和滞后期的相关关系。
for (i in 1:n) {
for (j in 1:n.var) {
c\_li <- leadlag(yc\_li\[, i\], yc_li\[, j\], maxLeadLag)
c\_hp <- leadlag(yc\_hp\[, i\], yc_hp\[, j\], maxLeadLag)
c_bp
c_bn
c_yd
for (k in 1:5) {
ynamesLong\[(cnt + k), 1\] <- paste(ynames.tmp)
}
cnt <- cnt + 5绘制结果。
# 线性趋势
barplot(corrStylizedFact)
box()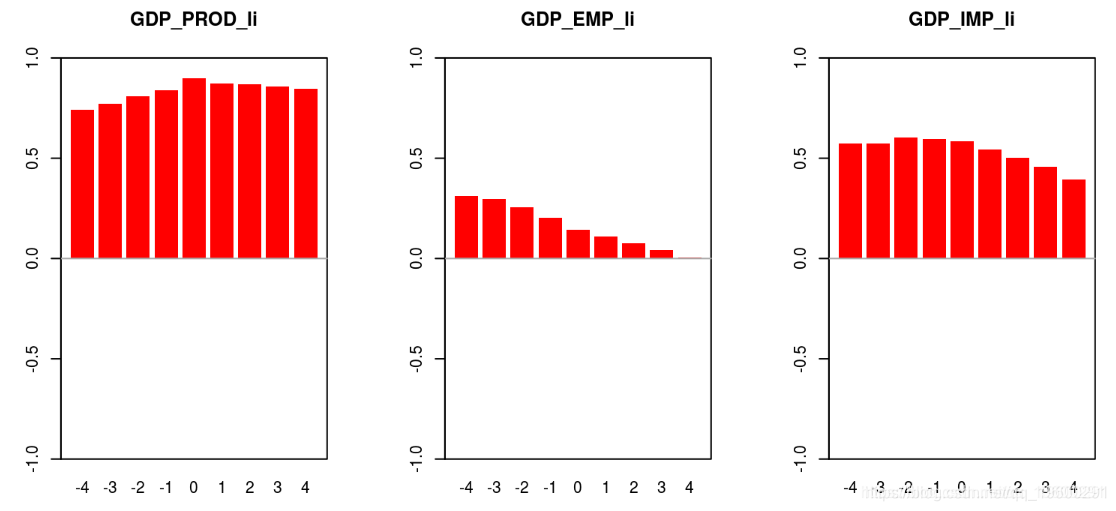
# hp滤波器
op <- par(mfrow = c(1, 3))
barplot(corrStyli, ylim = c(-1, 1))
box()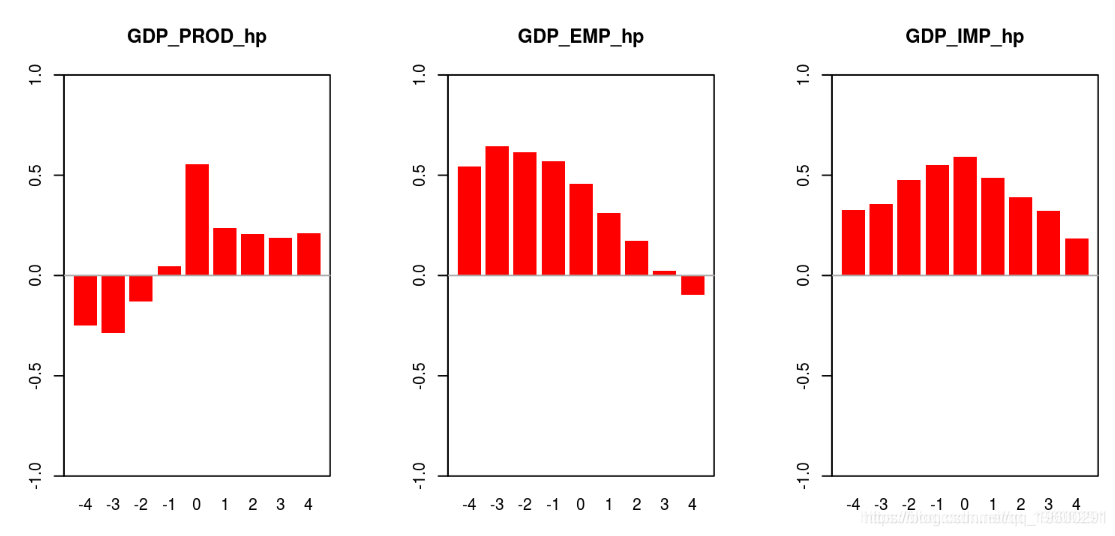
# beveridge nelson 分解
barplot(coracts, ylim = c(-1, 1), col = "red")
box()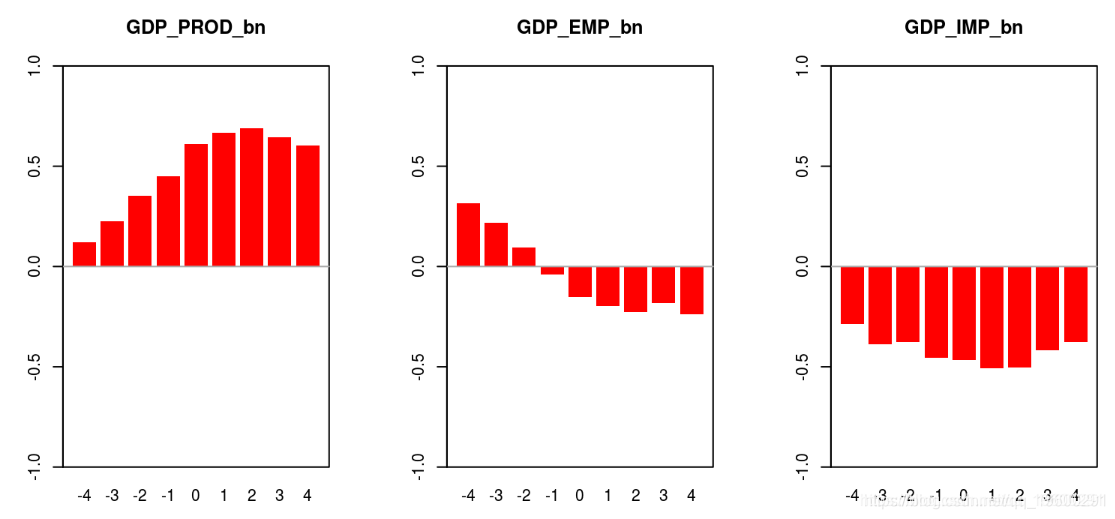

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!




 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究



