“获胜概率”的实时计算（或估计）很困难。
我们经常在足球比赛中，在选举中看到这种情况。
考虑经典的多项选择考试。在每个问题之后，想象您尝试计算学生通过考试的概率。
-
加法定律
几个互斥事件中任何一个发生的概率是各个事件发生的概率之和。
-
相乘定律
一系列独立事件都发生的概率是每个独立事件概率的乘积。
有了这两个工具，就足以回答日常生活中大部分关于“几率是多少”的问题。
当一个统计学家说出”1/10的可能性”这类话时，他就是对未来进行了一次预测。
这或许是对一系列永远都无法检验的事件所做的假设性陈述，或许是对即将发生的事件不掺半点水分的如实解说。
不管是哪种，他都是在对可能的结果进行统计学解释，所有的统计学家所说的话都无非如此。
如果你能够理解以下表述，那么你就具有了像统计黑客一样行动和思考的必备能力：
“如果有10件事情可能要发生，并且这10件事情发生的可能性相等，那么这10件事中任何一件发生的几率是1/10。”
科学研究中充满了可用统计来回答的问题，当然，还有概率定律的运用，但在实验室之外还有很多难题，比愚笨陈旧的科学问题更加重要的问题，比如骰子游戏。
假设你是一名业余赌徒，家里的小孩想要双新鞋子。你下次掷出一对骰子的值会决定你的未来。那你也许想知道骰子扔出各种结果的可能性，而且是非常准确地知道这种可能性！
只凭这两件概率工具，就能回答你可能问到的三类最重要的概率问题。
你提出的问题很可能是以下三种类型之一。
-
下一步出现某个特定结果的可能性是多少？比如，下面会掷出一个7吗？
-
下一步出现某组结果的可能性是多少？比如，下面会出现7或11吗？
-
下一步出现一系列结果的可能性是多少？比如，一对没被动过手脚的骰子真的能够整晚都不出现7吗（我说的是永远都不出现）？我的意思是，那真的可能吗？可能吗？！
在这里考虑我们有 50 个问题的情况。学生在答对 25 个以上时通过。为了模拟，我假设学生在每个问题上只掷硬币，我有 n 个学生，50 个问题
M=matrix
令 Xi,j 表示学生 i在问题 j 的分数。让 Si,j 表示累积分数，即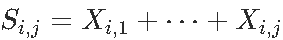 
. 在第 j 步，我可以使用 T^i,j =50×Si,j /j 对最终得分进行某种预测。这是代码
S=apply B
我们可以绘制它
plot(B) abline for(i in 2:n) lines lines
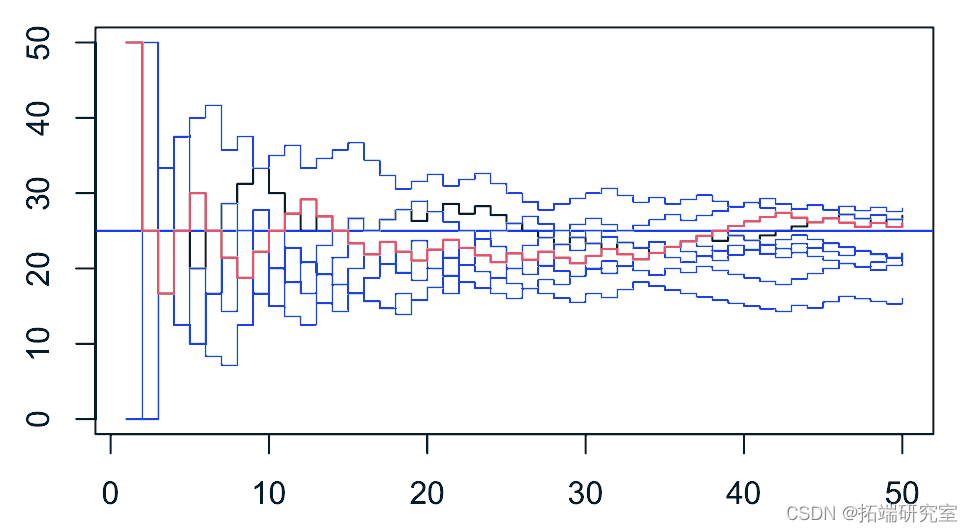
但这 只是 对每一步的最终分数的预测。这不是通过概率的计算！
如果在 j 个问题之后，学生有 25 个正确的答案，那么概率应该是 1——即如果 Si,j ≥25。另一个简单的例子是：如果在j题之后，他直到最后都答对了，他能得到的分数不够，他就会失败。这意味着如果 Si,j +(50−i+1)<25，概率应该是 0。否则，要计算成功的概率，就很简单了。它是当成功的概率实际上是 Si,j /j 时，在 50-j 个问题中获得至少 25-Si,j 正确答案的概率。我们认识到二项式分布的生存概率。然后代码很简单
for(i in 1:50){
for(j in 1:n){
if() P\[i,j\]=1
if() P\[i,j\]=0
if()B\[i,j\]=1-pbinom
所以如果我们绘制它，我们得到
plot(P abline for(i in 2:n) lines lines
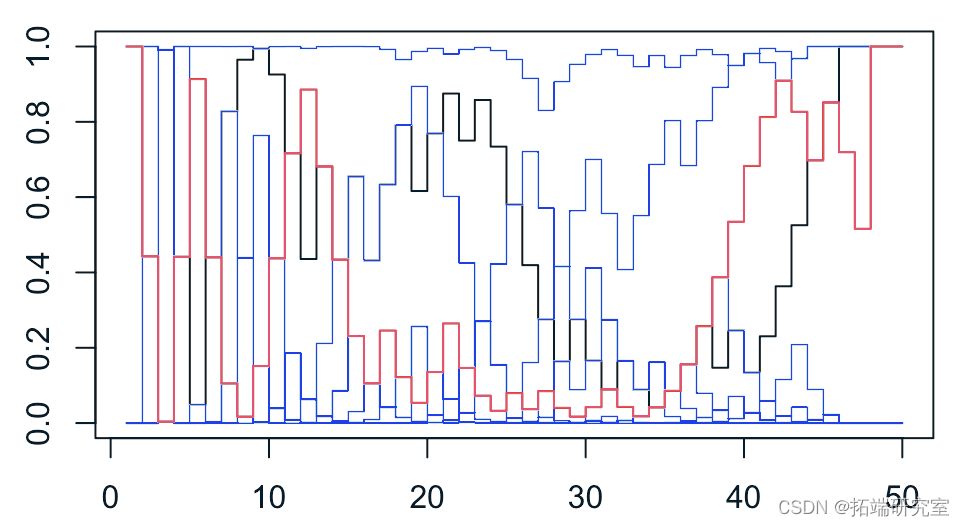
这比我们之前获得的曲线更不稳定！所以，计算“获胜概率”是一项复杂的工作！
随时关注您喜欢的主题
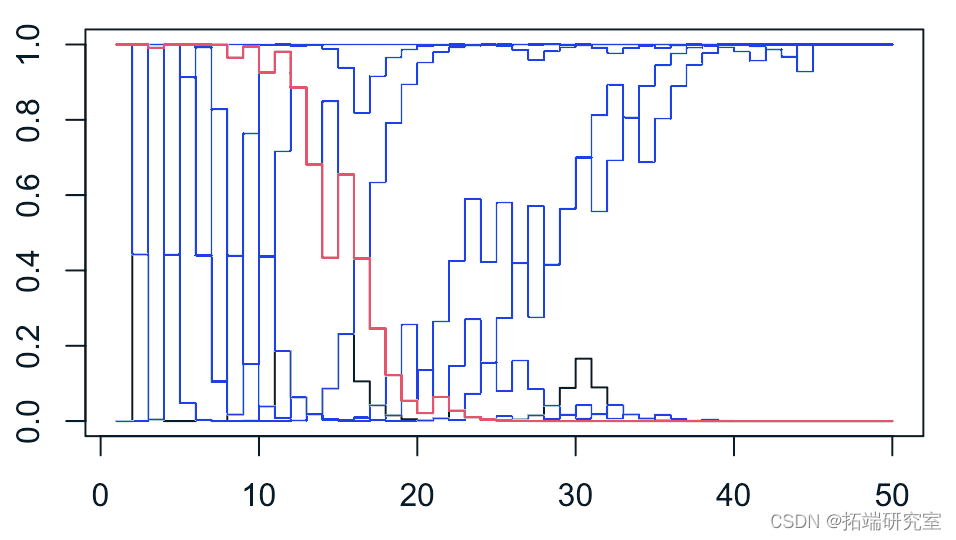
当然，如果我的学生不抛硬币，情况就略有不同……这是我们得到的结果，如果一半的学生是好的（有2/3的概率答对问题），一半是不好的（1/3的概率）。
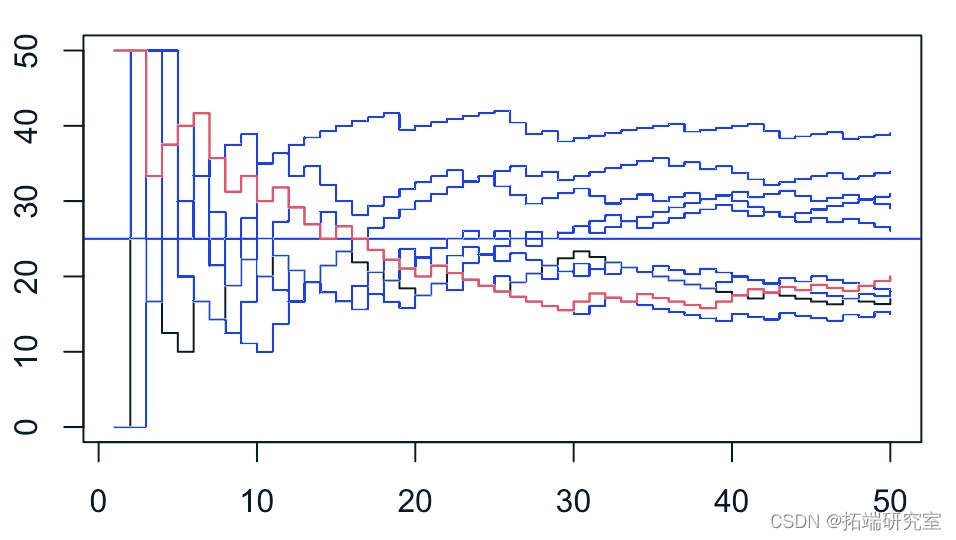
如果我们看通过的概率，我们通常不必等到最后（50道题）就知道谁通过了，谁没通过
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
【视频讲解】Python比赛LightGBM、XGBoost+GPU和CatBoost预测学生在游戏学习过程表现|数据代码分享
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
R语言SVM模型用大学生行为数据对助学金精准资助预测ROC可视化
