Double-no-touch(DNT)选项是二元期权,在到期时支付固定金额的现金。我们将展示两种不同的方式来定价包含两种不同定价方法的DNT。


首先,我们将尝试使用正常参数,看看收敛速度有多快:
print(dnt1(100,10,120,80,0.1,0.25,0.05,0.03,20,TRUE))

以下屏幕截图显示了上述代码的结果:

另一个问题是,如果我们选择极高的ü或极低的L,则会出现计算错误,然而,类似于波动性的问题。如果我们将ü更高或更低,则DNT的价格应该增加。
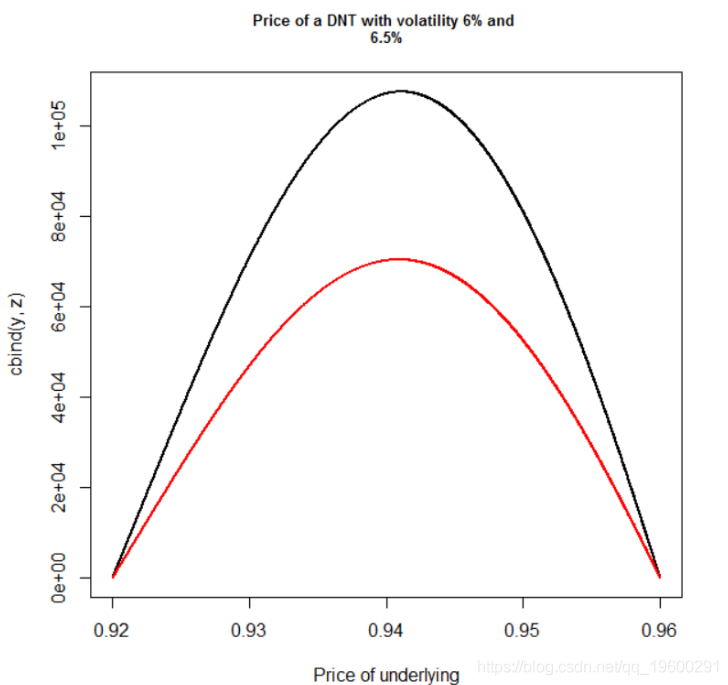
以下代码绘制了底层价格的图表:
for(i in 1:2000){
y [i]
z [i]
}
matplot(x,cbind(y,z),type =“l”,lwd = 2,lty = 1,
main =“ “,cex.main = 0.8,xlab =” “)

以下输出是上述代码的结果:
可以清楚地看到,即使波动率的微小变化也会对DNT的价格产生巨大影响。
大多数最终用户认为最大的风险是现场接近触发点。这是因为最终用户真的以二进制方式考虑二元期权。
我们可以使用GetGreeks函数来估计维加,γ,δ和有峰。
对于γ,我们可以通过以下方式使用GetGreeks函数:
GetGreeks
all_args1
all_args1 [[arg]]
all_args2 [[arg]]
(do.call(FUN,all_args1) -
do.call(FUN,all_args2))/(2 * epsilon)
}
Gamma
arg1
arg2
arg3
y1
y2
(y1 - y2 )/(2 * epsilon)
}
delta
(i in 1:200){ delta [i]
x [i],1000000,0.96,0.92,0.06,0.5,0.02 ,-0.02)vega [i]
x [i],1000000,0.96,0.92,0.06,0.5,0.0025,-0.025)theta [i]
x [i],1000000,0.96,0.92,0.06,0.5,0.0025, - 0.025)gamma [i]
}
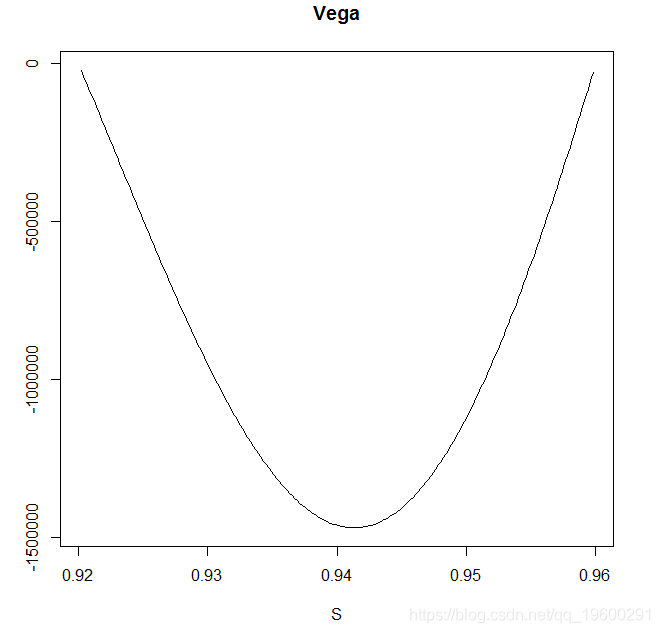
windows()plot(x,vega,type =“l”,xlab =“S”,ylab =“”,main =“Vega”)


以下图表是上述代码的结果:
在看了价值图表之后,DNT的增量也非常接近直觉; 如果我们接近更高的障碍,我们的增量变为负值,如果我们接近较低的障碍,增量变为正值如下:
windows()
plot(x,delta,type =“l”,xlab =“S”,ylab =“”,main =“Delta”)

对于动态套期保值者来说,这意味着在价格上涨后买入一些澳元兑美元,并在价格下跌后卖出相同的金额。
可以通过如下的伽玛来描述增量的变化:
windows()
plot(x,gamma,type =“l”,xlab =“S”,ylab =“”,main =“Gamma”)

负伽玛意味着如果该点上升,我们的增量正在减少,但如果该点下降,我们的增量增加。
windows()
plot(x,theta,type =“l”,xlab =“S”,ylab =“”,main =“Theta”)

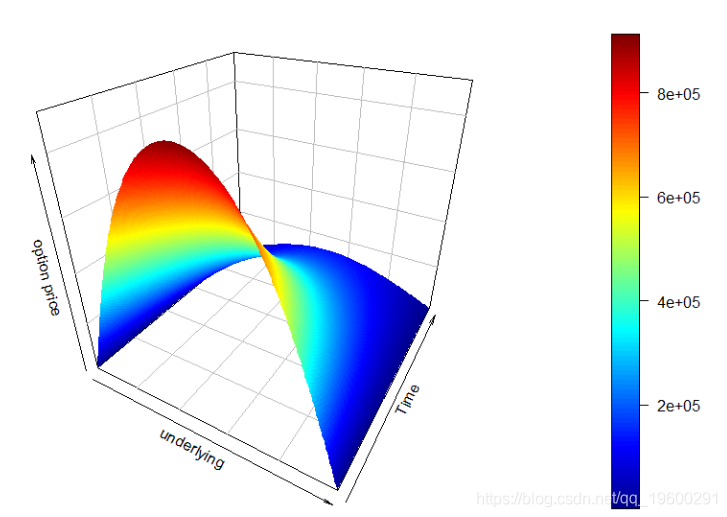
我们之前已经介绍了布莱克 – 斯科尔斯表面; 现在,我们可以详细介绍一下。代码如下:
BS_surf
n
k
m
for(i in 1:n){
for(j in 1:k){
l
m [i,j]
}
}
persp3D(z = m,xlab =“underlying”,ylab =“Time”,
}
上面的代码给出了以下输出:

Double-no-touch 模拟
DNT价格在2014年第二季度的变化情况如何?
option_price
for(i in 1:n){ option_price [i] U = 0.9600,L = 0.9200,sigma = 0.06,T = t [i] /(60 * 24 * 365), r = 0.0025,b = -0.0250)} a
b
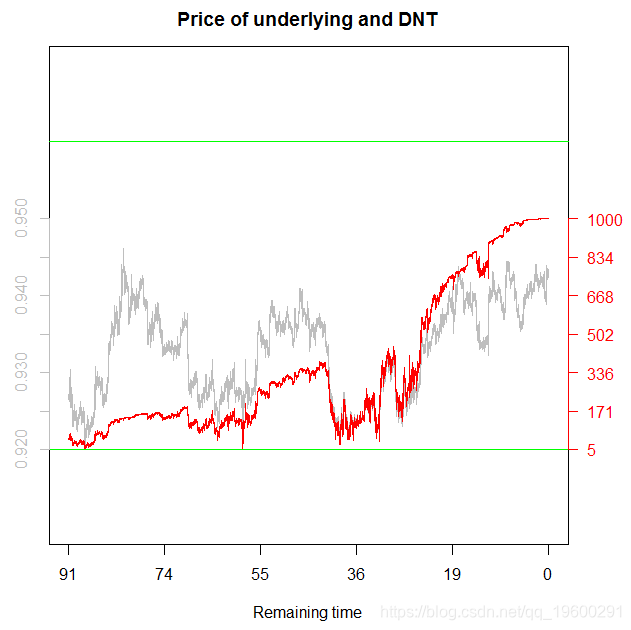
option_price_transformed =(option_price - a)* 0.03 /(b - a)+ 0.92 par(mar = c(6,3,3,5 ))matplot(cbind(underlying,option_price_transformed),type = “l”,


以下是上述代码的输出:
DNT的价格在右轴显示为红色(除以1000),实际的AUDUSD价格在左轴显示为灰色。
dnt1(0.9203,1000000,0.9600,0.9200,0.06,59 / 365,0.0025,-0.025)
[1] 5302.213
比较此5302美元至最初的48564美元期权价格
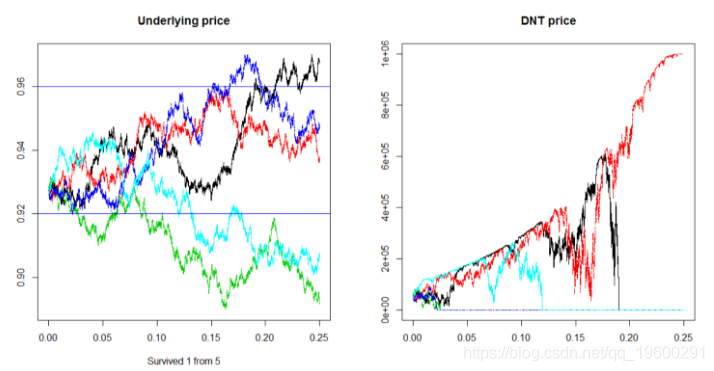
在下面的模拟中,我们将展示一些不同的轨迹所有这些都是从与4月1日黎明时相同的0.9266澳元兑美元现货价格开始,我们将看到其中有多少人保持在(0.9200。0.9600)区间内,为简单起见,我们将使用与我们用于定价DNT相同的6%波动率来模拟几何布朗运动:
library(matrixStats)
DNT_sim
L = 0.92,N = 5){
option_price
matplot(t,option_price,type =“l”,main =“DNT price”,
xlab =“”,ylab =“”)}
set.seed(214)
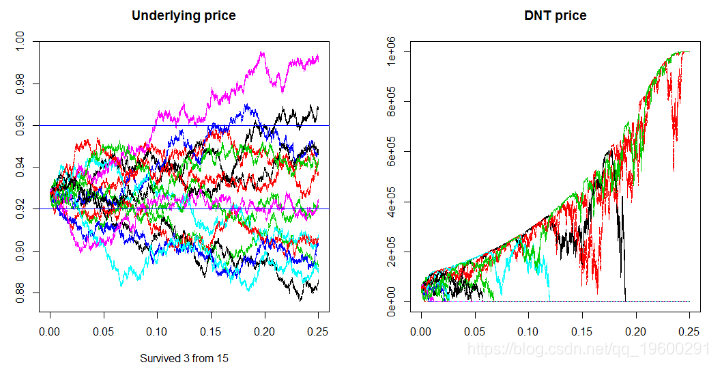
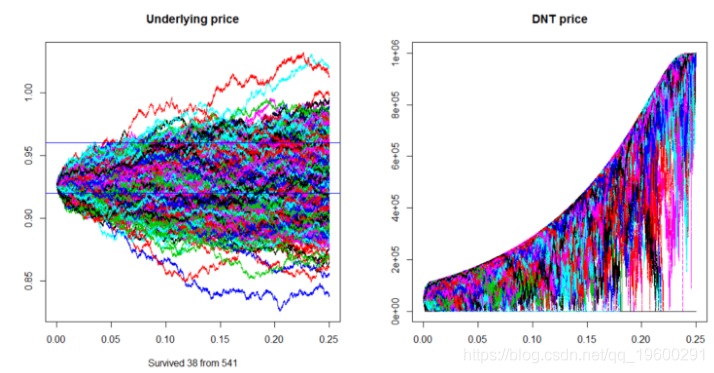
system.time(DNT_sim())
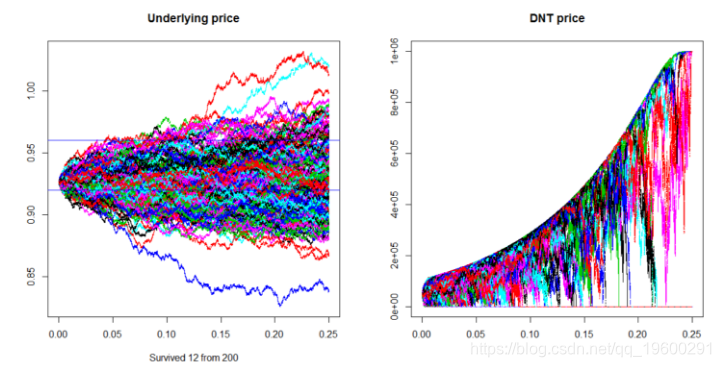

以下是上述代码的输出:

还有问题吗?联系我们!
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
