划分聚类 是用于基于数据集的相似性将数据集分类为多个组的聚类方法。
分区聚类，包括：
- K均值聚类 （MacQueen 1967），其中每个聚类由属于聚类的数据点的中心或平均值表示。K-means方法对异常数据点和异常值敏感。
- K-medoids聚类或PAM（Partitioning Around Medoids，Kaufman和Rousseeuw，1990），其中，每个聚类由聚类中的一个对象表示。与k-means相比，PAM对异常值不太敏感。
- CLARA算法（Clustering Large Applications），它是适用于大型数据集的PAM的改进。
可下载资源
对于这些方法中的每一种，我们提供：
- 基本思想和关键概念
- R软件中的聚类算法和实现
- R用于聚类分析和可视化的示例
给定n个数据点的数据集合，构建数据集合的出K个划分，每个划分代表一个类别，2<k<sqrt(n)。算法思想，划分法需要预先指定聚类数目和聚类中心，计算每个点与其他点的距离，对于每个数据点都有n-1个距离值，对这些距离值进行排序，找出最接近的数据点，算出这些距离的和值。并进行下次迭代，这时数据中兴点位置改变，继续按照上方的步骤，逐步降低目标函数的误差值，直到目标函数值收敛时，得到最终聚类的结果。逐步对聚类结果进行优化、不断将目标数据集向各个聚类中心进行重新分配以获最优解。代表算K-means,K-medoids.
setp1:指定K个聚类中心
setp2:(每一个数据点与初始聚类中心的距离)
setp3:（对每一个数据点x,找到最近的C（聚类中心），x分配到新的类C中）
setp4:（更新聚类中心点)
setp5:（计算每一类的偏差）
setp6:判断偏差是否小于阈值（自己设定），不小于则返回setp2
当聚类是密集的，而聚类之间区别明显时，K—Means算法的效果较好。另外，对处理大数据集，该算法是高效率的，因为它的复杂度是，其中，n是所有对象的数目，K是聚类的数目，t是迭代的次数。通常且。但是，K—Means算法只有在聚类的平均值被定义的情况下才能使用。如果处理符号属性的数据并不适用。K—Means算法对初始聚类中心和样本的输入顺序敏感，对于不同的初始聚类中心和样本输入顺序，聚类结果会有很大差别。由于采用迭代更新的方法，所以当初始聚类中心落在局部值最小附近时，算法容易生成局部最优解。另外，算法的效果受孤立点的影响很大。
优点：1简单，易于理解和实现；2，时间复杂度低3.聚类中心用各类别中所有数据的平均值表示k-means方法的缺陷1，需要对均值给出定义,2，需要指定要聚类的数目；3，一些过大的异常值会带来很大影响；4，算法对初始选值敏感；5，适合球形聚类6.结果好坏依赖于对初始聚类中心的选择、容易陷入局部最优解、对K值的选择没有准则可依循、只能处理数值属性的数据、聚类结构可能不平衡。
数据准备：
my_data <- USArrests
# 删除所有缺失值（即NA值不可用）
my_data <- na.omit(my_data)
# 标准化变量
my_data <- scale(my_data)
# 查看开始3行
head(my_data, n = 3)
## Murder Assault UrbanPop Rape
## Alabama 1.2426 0.783 -0.521 -0.00342
## Alaska 0.5079 1.107 -1.212 2.48420
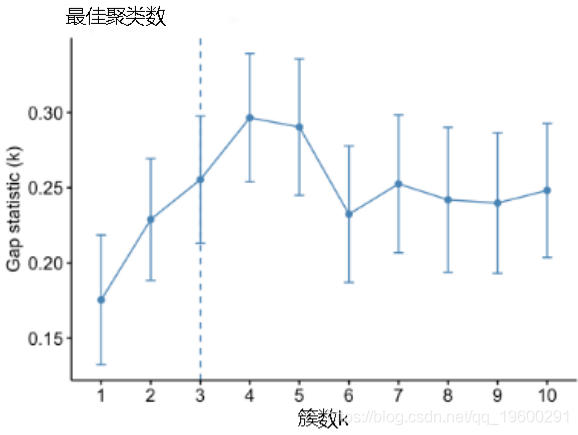
## Arizona 0.0716 1.479 0.999 1.04288确定k-means聚类的最佳聚类数：
fviz_nbclust(my_data, kmeans,
method = "gap_stat")## Clustering k = 1,2,..., K.max (= 10): .. done
## Bootstrapping, b = 1,2,..., B (= 100) [one "." per sample]:
## .................................................. 50
## .................................................. 100
fviz_cluster(km.res, data = my_data,
ellipse.type = "convex",
palette = "jco",
repel = TRUE,
ggtheme = theme_minimal())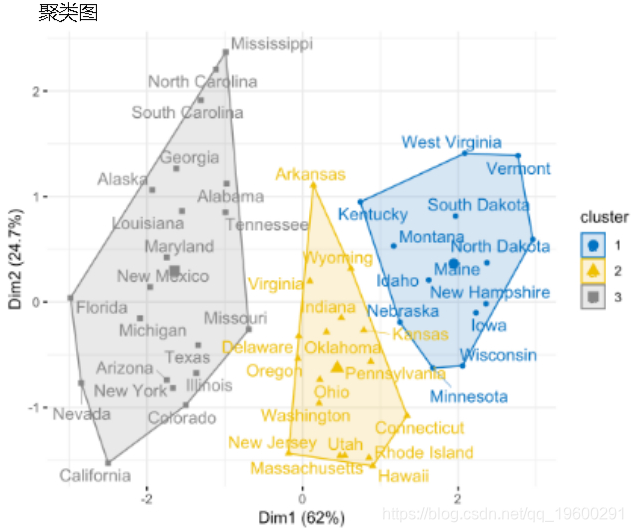
同样，可以如下计算和可视化PAM聚类：
pam.res <- pam(my_data, 4)
# 可视化
fviz_cluster(pam.res)
R语言K-Means(K均值）和层次聚类算法对微博用户特征数据研究
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
R语言代做编程辅导和解答GLM Coursework
