在我今天参与的一个讨论中,提出了一个问题,即在具有单个连续预测器的线性回归模型中R平方如何/是否取决于预测变量的方差。这个问题的答案当然是肯定的。
可视化
我们还可以在R中轻松地可视化前面的概念。我们首先从具有非常大的样本大小的线性模型中模拟数据:
n < - 10000 x < - 100 * runif(n) y < - x + rnorm(n)
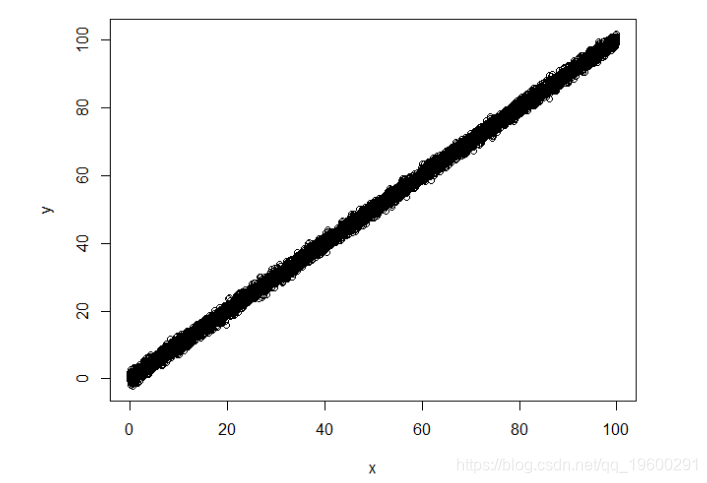

我们有: Y对X,对X没有限制
拟合相应的线性模型证实了这一点:
summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-4.1295 -0.6794 -0.0023 0.6879 3.5579
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0068489 0.0204500 0.335 0.738
x 0.9999752 0.0003534 2829.539 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.015 on 9998 degrees of freedom
Multiple R-squared: 0.9988, Adjusted R-squared: 0.9988
F-statistic: 8.006e+06 on 1 and 9998 DF, p-value: < 2.2e-16

给出R平方0.9988。
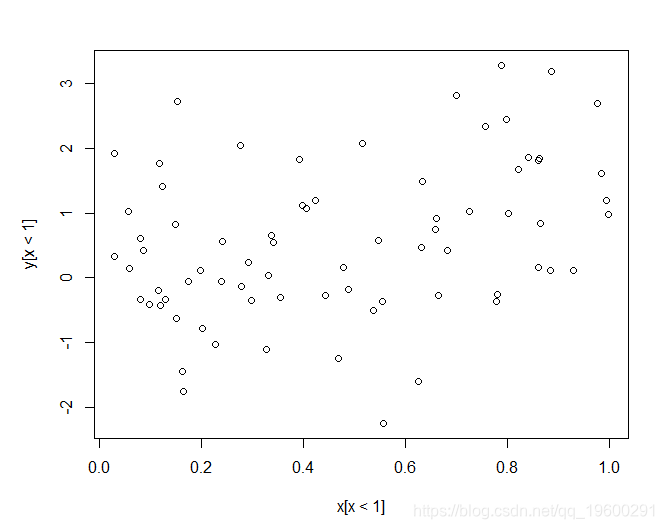

接下来,我们再次绘制数据,
summary(lm(y[x<1]~x[x<1]))
Call:
lm(formula = y[x < 1] ~ x[x < 1])
Residuals:
Min 1Q Median 3Q Max
-2.93421 -0.73513 -0.09459 0.69282 2.59506
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0893 0.2432 -0.367 0.71459
x[x < 1] 1.3960 0.4386 3.183 0.00215 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.121 on 72 degrees of freedom
Multiple R-squared: 0.1233, Adjusted R-squared: 0.1112
F-statistic: 10.13 on 1 and 72 DF, p-value: 0.002155
R平方值低得多,为0.1233。
非常感谢您阅读本文,有任何问题请在下面留言!
1
1
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。





