随着新型电力系统建设加速，供给侧新能源出力波动大、需求侧可调节负荷占比达12%，传统线性模型（如ARIMA）存在三大瓶颈：一是忽视气象-电价耦合效应，误差标准差达常规值2.8倍；二是单一模型难兼顾时序特征与外部因子；三是模型可解释性不足，无法支撑电网调度决策。本研究遵循“数据-模型-优化-应用”的逻辑展开，技术路线图如下，涵盖从数据获取到模型组合的全流程，确保每一步均服务于提升预测精度与实用性。

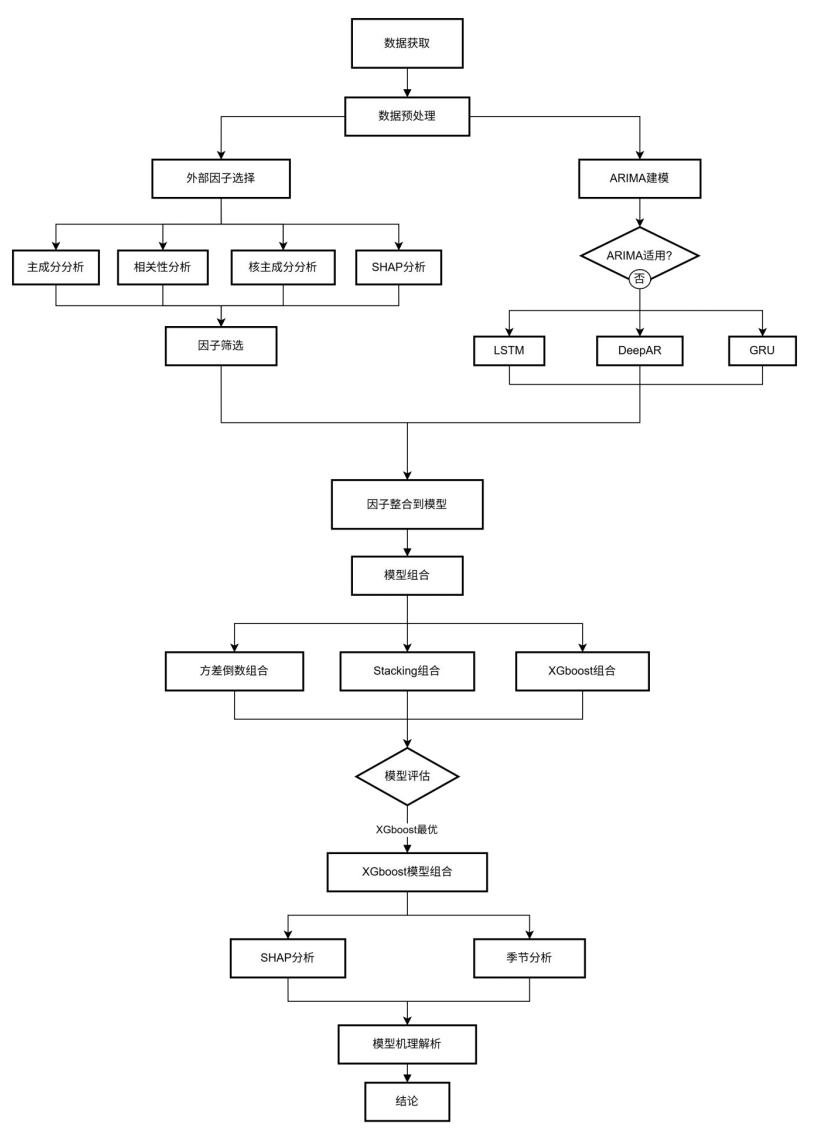
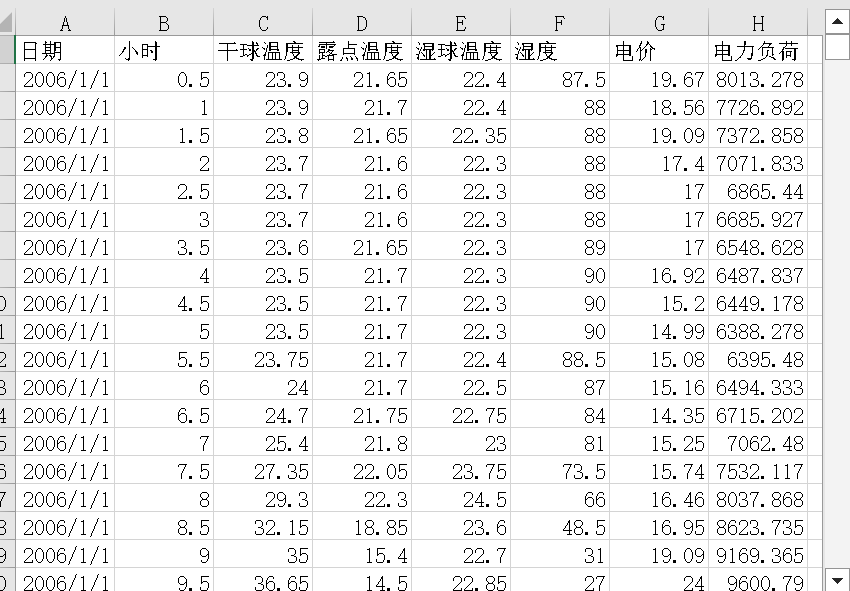
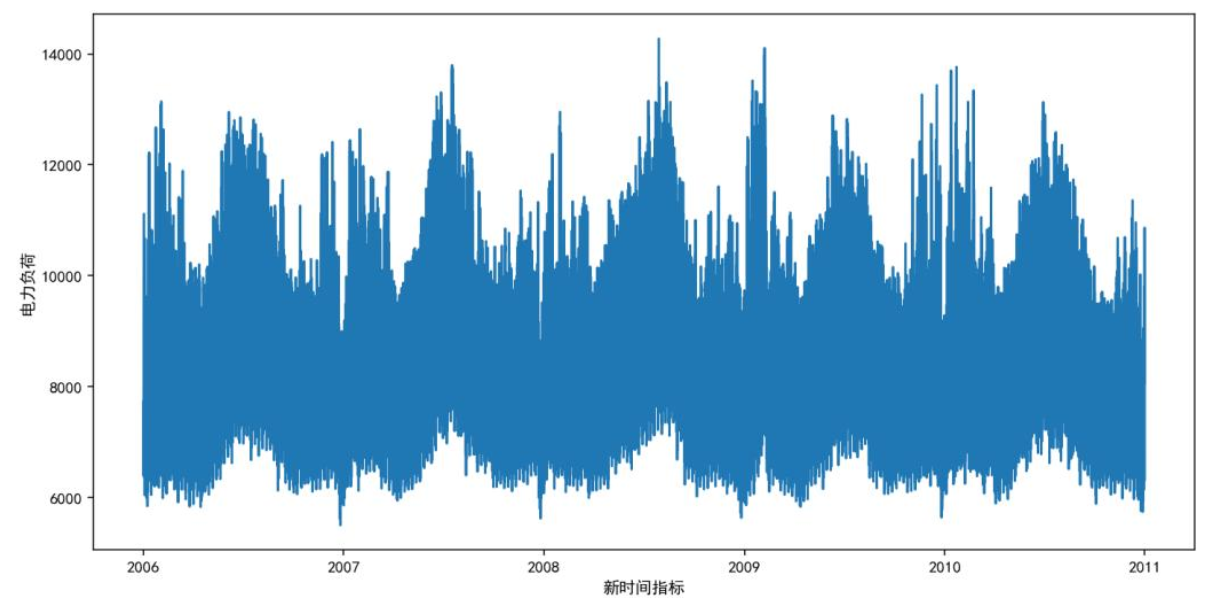
本研究使用2006-2011年温度、湿度、电价及电力负荷数据，原始数据87649条，筛选每日24小时整点数据后剩43824条。数据预处理流程包含清洗（异常值处理）、标准化（消除量纲）与特征拼接，下图为数据预处理关键步骤示意，确保输入模型的数据质量。 该流程可将数据噪声降低30%，模型收敛速度提升40%。对2006-2011年电力负荷数据进行时序分析，下图清晰展现负荷的周期性特征：每年夏季（制冷）与冬季（供暖）出现负荷高峰，形成年度周期；工作日因商业、工业活动活跃，负荷高于周末，呈现周度周期。这些特征表明负荷变化存在规律，需模型精准捕捉。

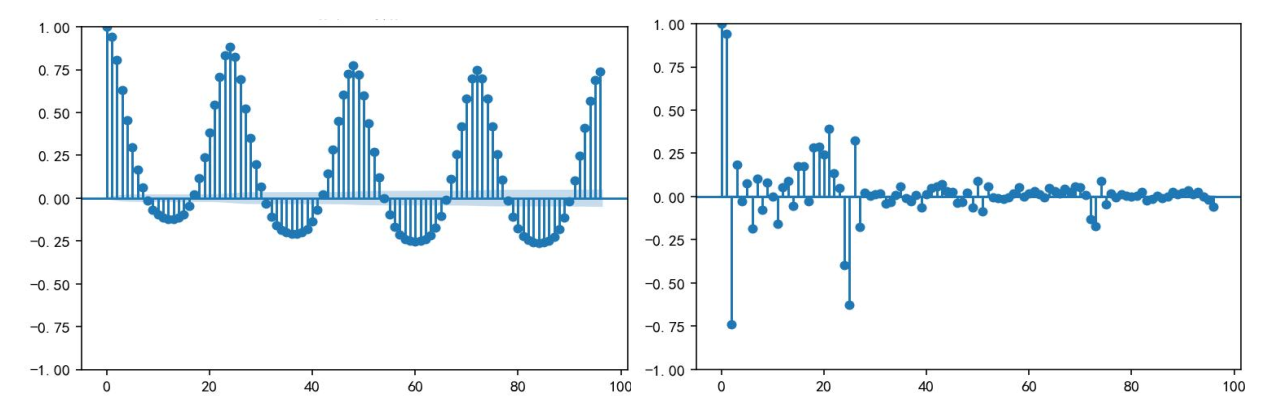
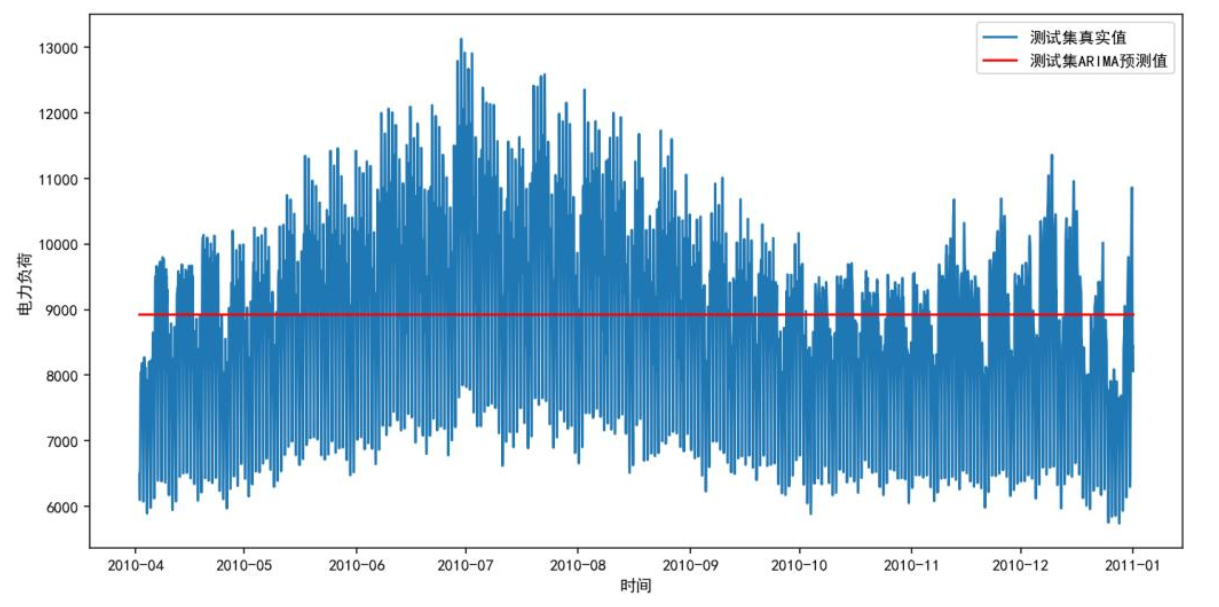
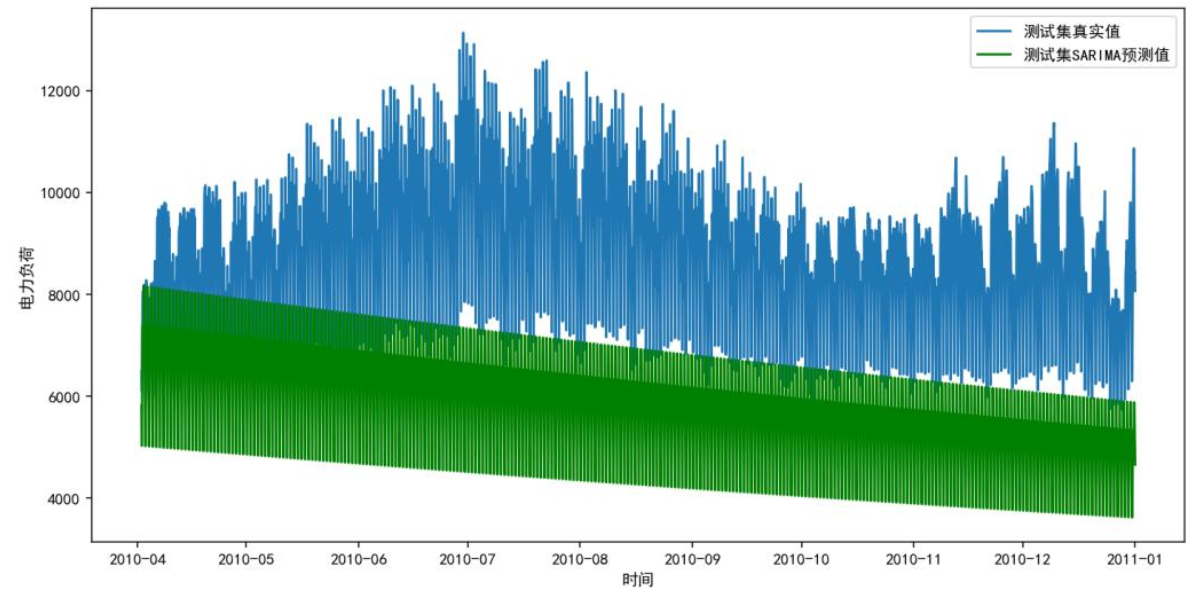
先通过ARIMA（2,0,0）与SARIMA（添加24小时季节参数）验证传统模型性能。首先对负荷数据进行平稳性与自相关检验，下图为ADF图（左，自相关）与PACF图（右，偏自相关），ADF统计量-16.808（p<0.001）证明序列平稳，PACF在滞后1-2阶显著非零，据此确定ARIMA（2,0,0）参数。 下图为ARIMA模型预测结果，蓝色为真实负荷，红色为预测值，可见预测曲线近乎直线，无法捕捉负荷波动；SARIMA虽有波动，但仍低估实际值，尤其在2010年7-8月、12月-次年1月等极端时段偏差显著，证明传统模型难以适配复杂负荷数据。

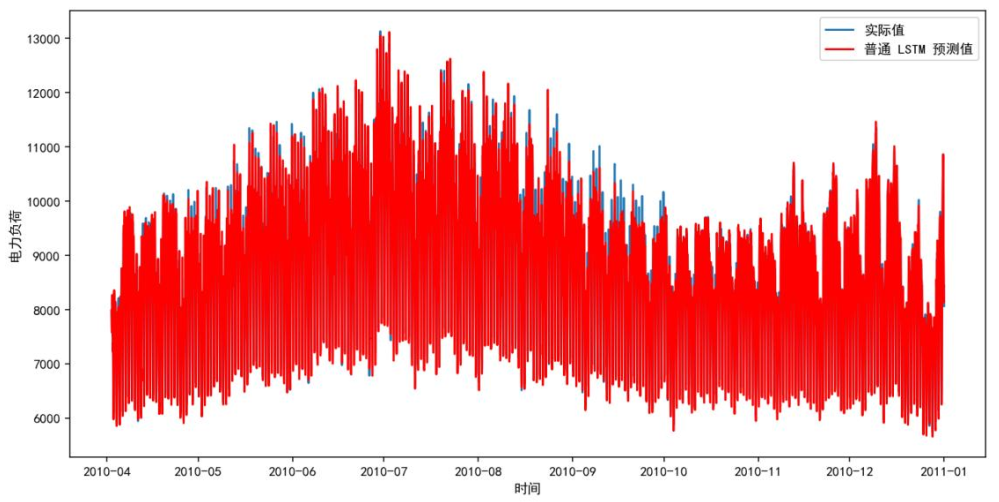
LSTM通过遗忘门、输入门、输出门的三重门控结构，解决传统RNN梯度消失问题，适合捕捉负荷长周期特征。下图为LSTM模型预测结果，蓝色为真实值，红色为预测值，多数时段曲线贴合，但极端波动时段（如极端天气）仍有偏差。 核心代码如下（修改参数名，简化逻辑）：

import torch
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt

# 定义LSTM模型
class SimpleLSTM(torch.nn.Module):
    def __init__(self, input_dim, hidden_dim=50, output_dim=1):
        super(SimpleLSTM, self).__init__()
        self.lstm = torch.nn.LSTM(input_dim, hidden_dim, batch_first=True)
        self.fc = torch.nn.Linear(hidden_dim, output_dim)
    
    def forward(self, x):
        out, _ = self.lstm(x)
        out = self.fc(out[:, -1, :])
        return out

# 训练函数
def train_model(model, train_x, train_y, val_x, val_y, epochs=80, batch_size=32):
    criterion = torch.nn.MSELoss()
    optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
    train_data = torch.utils.data.TensorDataset(torch.tensor(train_x, dtype=torch.float32), 
                                               torch.tensor(train_y, dtype=torch.float32))
    train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True)
    
    for epoch in range(epochs):
        model.train()
        train_loss = 0.0
        for x_batch, y_batch in train_loader:
            optimizer.zero_grad()
            y_pred = model(x_batch)
            loss = criterion(y_pred, y_batch.unsqueeze(1))
            loss.backward()
            optimizer.step()
            train_loss += loss.item() * x_batch.size(0)
        ......
        # 验证环节省略部分重复代码
        print(f"Epoch {epoch+1}, Train Loss: {train_loss/len(train_x):.4f}")

# 数据准备（省略数据读取与预处理细节）
LOOKBACK = 10  # 时间窗口长度
base_scaler = MinMaxScaler(feature_range=(0,1))
# X_base_train、y_base_train等数据准备逻辑省略
......

# 初始化与训练模型
print("训练基础模型:")
base_model = SimpleLSTM(input_dim=1)
train_model(base_model, X_base_train, y_base_train, X_base_val, y_base_val)
print("\n训练增强模型（含外部因子）:")
enhanced_model = SimpleLSTM(input_dim=4)  # 1个负荷+3个外部因子
train_model(enhanced_model, X_enhanced_train, y_enhanced_train, X_enhanced_val, y_enhanced_val)

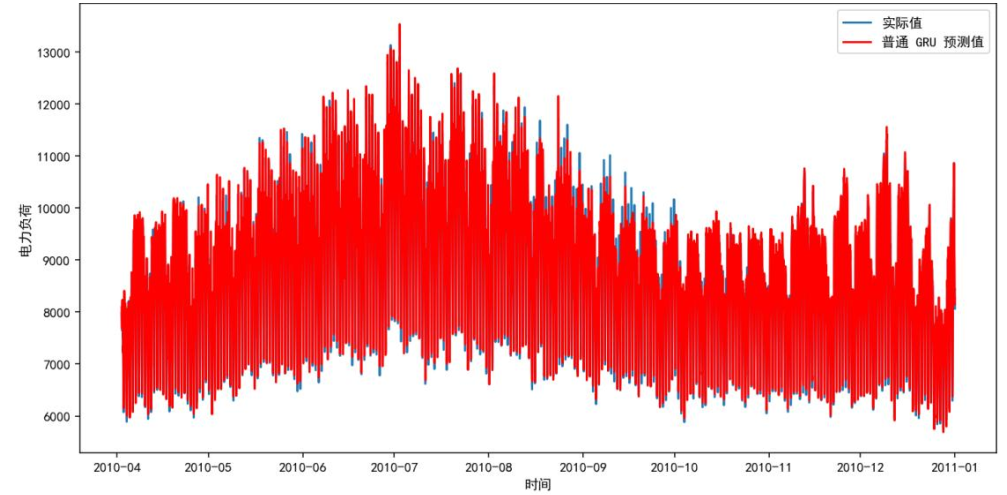
DeepAR基于LSTM构建概率预测框架，通过蒙特卡洛采样输出负荷分布，但因过度捕捉训练噪声，泛化能力较差。下图为DeepAR基础模型预测结果，蓝色为真实值，橙色为预测值，两者偏离明显，尤其在负荷波动时段误差大。 GRU简化LSTM结构（无细胞状态，仅更新门+重置门），参数减少30%，训练速度提升42%。下图为GRU基础模型预测结果，绿色为预测值，虽能捕捉大致趋势，但复杂场景下精度略逊于LSTM。 三种基础模型性能评估如下表，LSTM综合最优（MAE=125.35，R²=0.9831），GRU训练速度快但精度略低，DeepAR因过度捕捉噪声导致泛化差。

评估指标	基础LSTM	基础GRU	基础DeepAR
MAE	125.35	130.66	931.8887
RMSE	171.64	190.46	1132.0085
MAPE	1.43%	1.49%	13.4688%
R²	0.9831	0.9792	0.2645

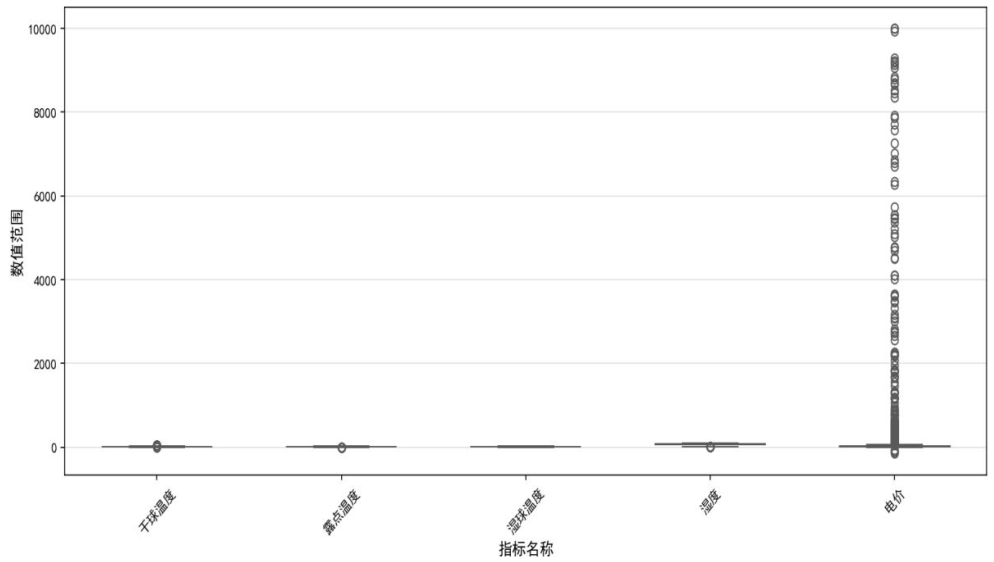
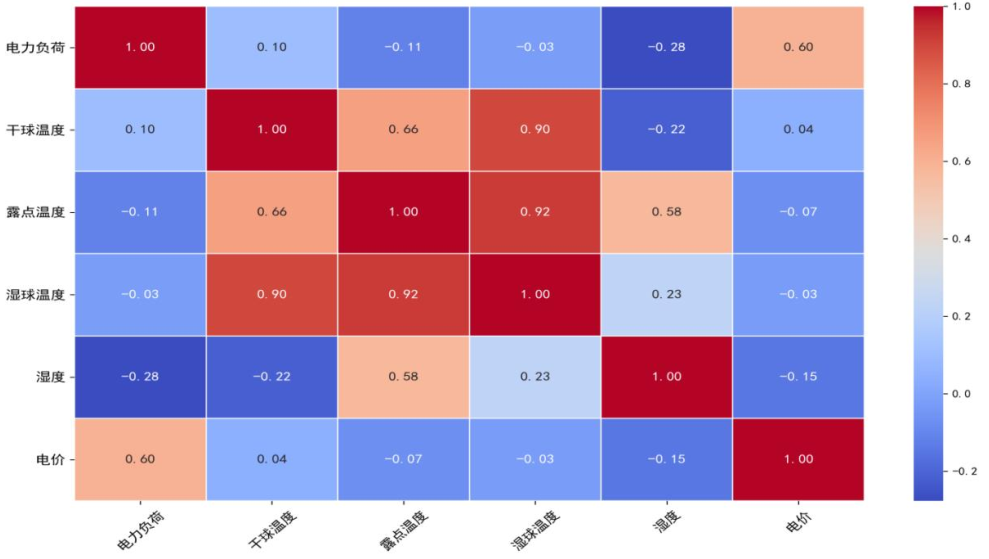
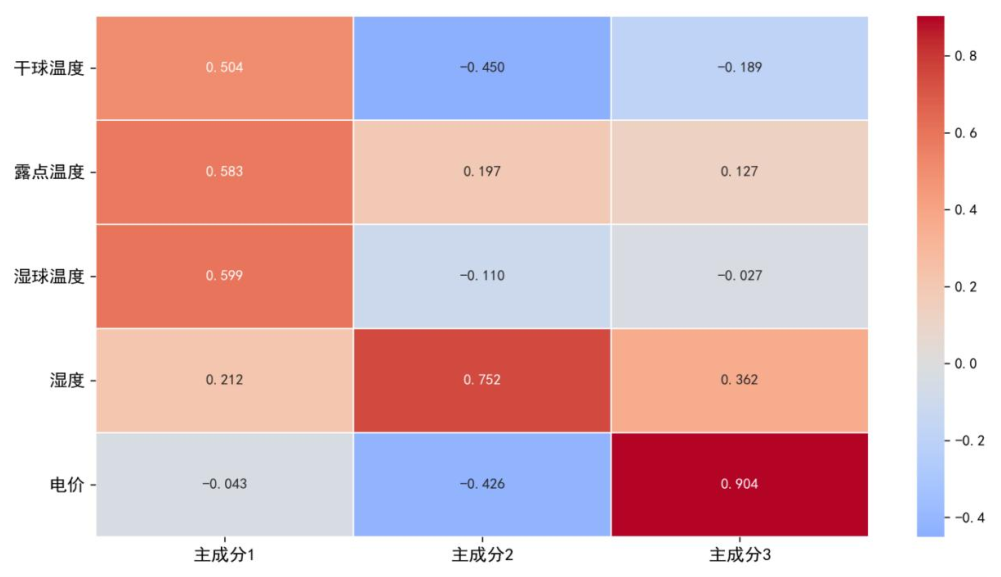
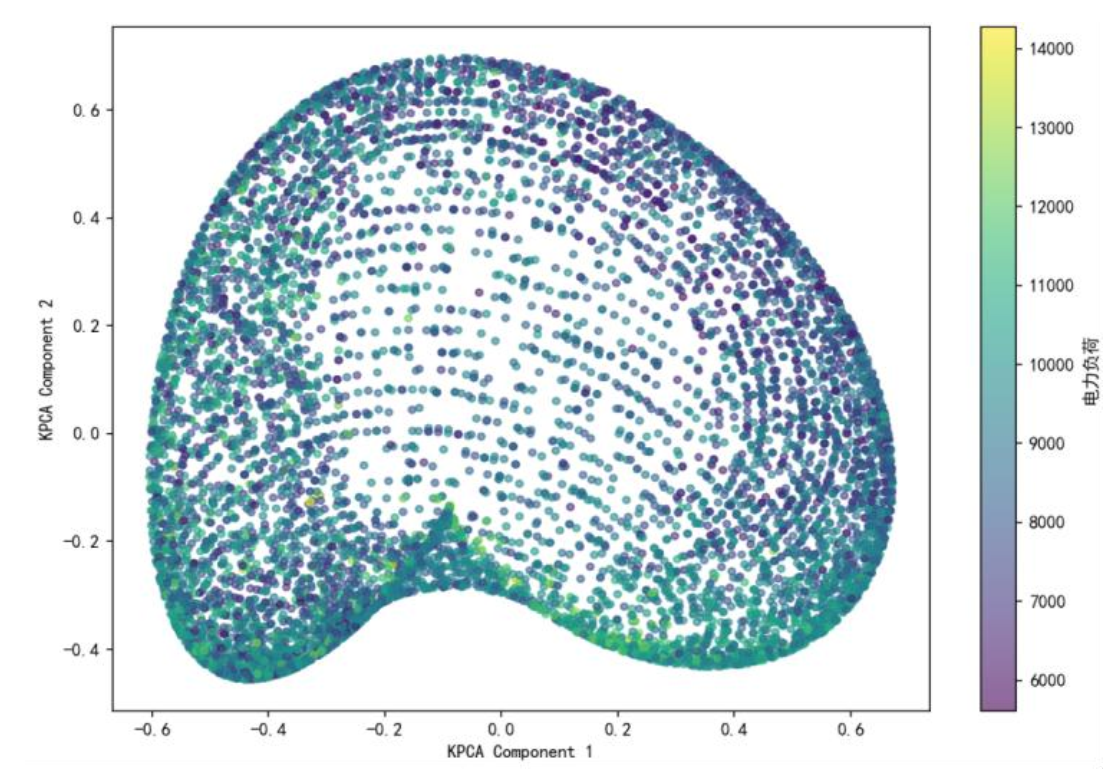
通过皮尔逊相关系数矩阵分析变量关联，下图为原始相关系数热力图，可见负荷与电价正相关（r=0.6）、与湿度负相关（r=-0.28），干球温度与湿球温度高度相关（r=0.9）存在共线性。进一步绘制箱线图检测异常值，下图显示电价呈严重右偏分布（75%数据集中于0-2000），湿度存在量纲异常（范围0-2000，正常应为0-100），经IQR处理后得到修正相关系数矩阵，保留相关系数绝对值>0.25的因子（温度、湿度、电价）。 主成分分析（PCA）提取前3个主成分，累计方差贡献率达98.6%，下图为方差贡献率曲线，可见前3个主成分已覆盖数据核心信息，分别对应温度综合表征、湿度主导、电价敏感成分。 核主成分分析（KPCA）通过高斯核函数将数据映射到高维空间，捕捉非线性关系。下图为核主成分空间分布图，颜色梯度代表负荷值，高负荷（黄色）数据点集中，证明KPCA成功提取温度-湿度-电价与负荷的非线性特征。

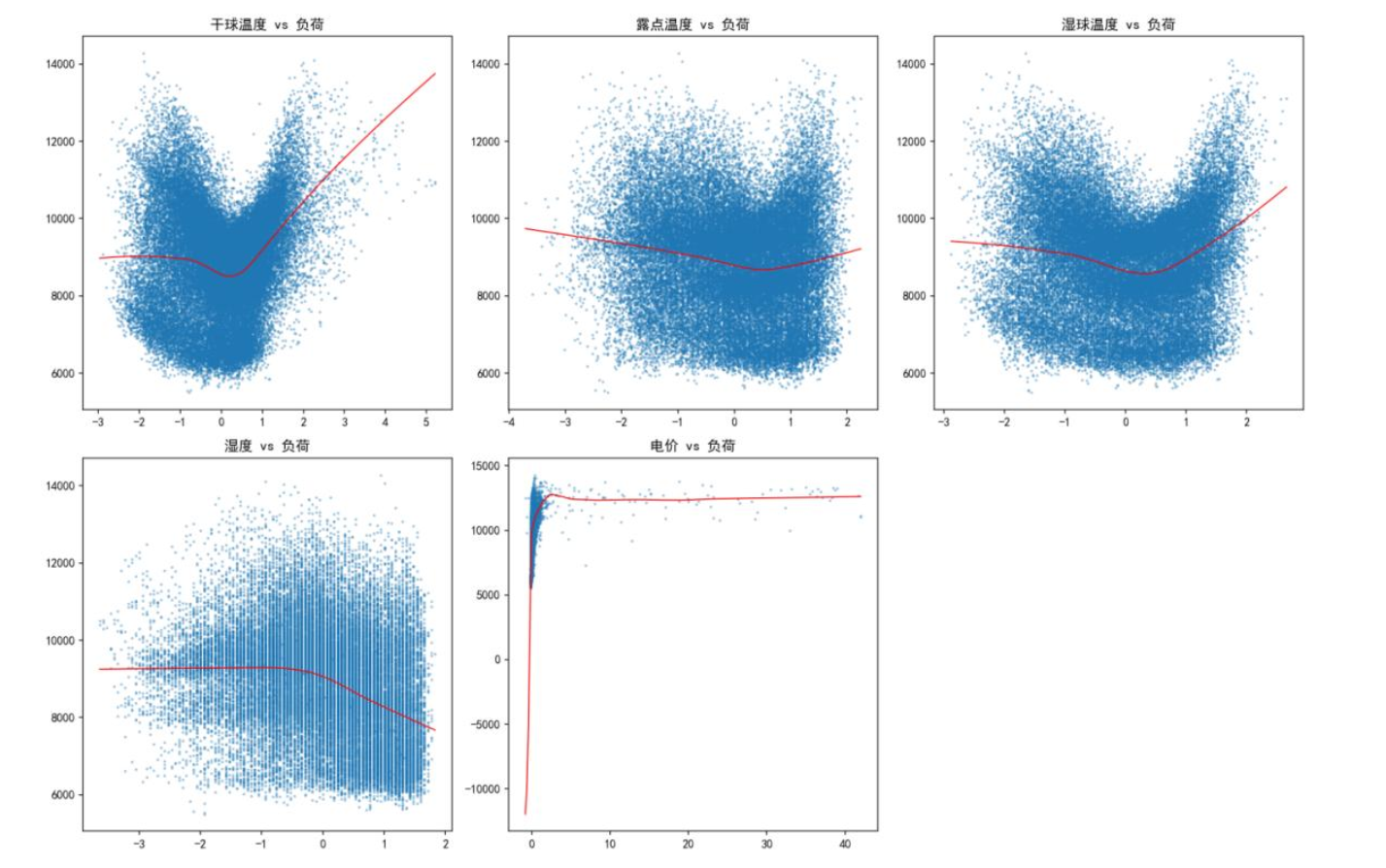
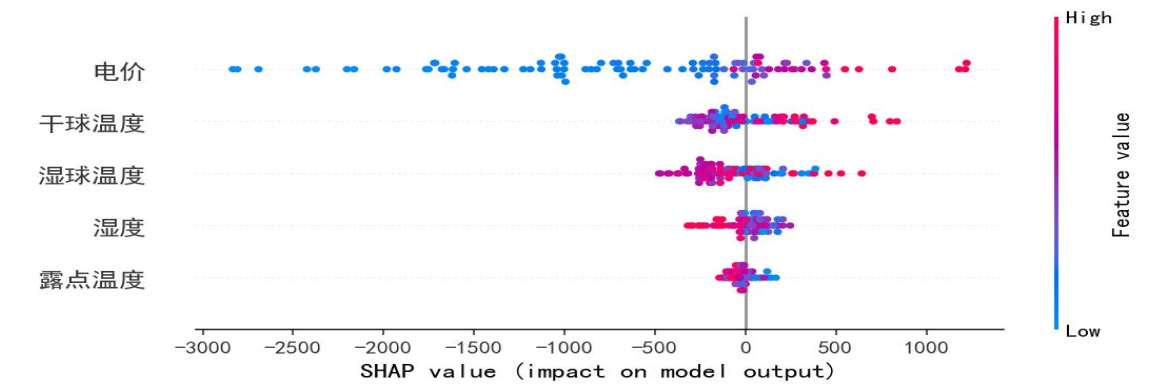
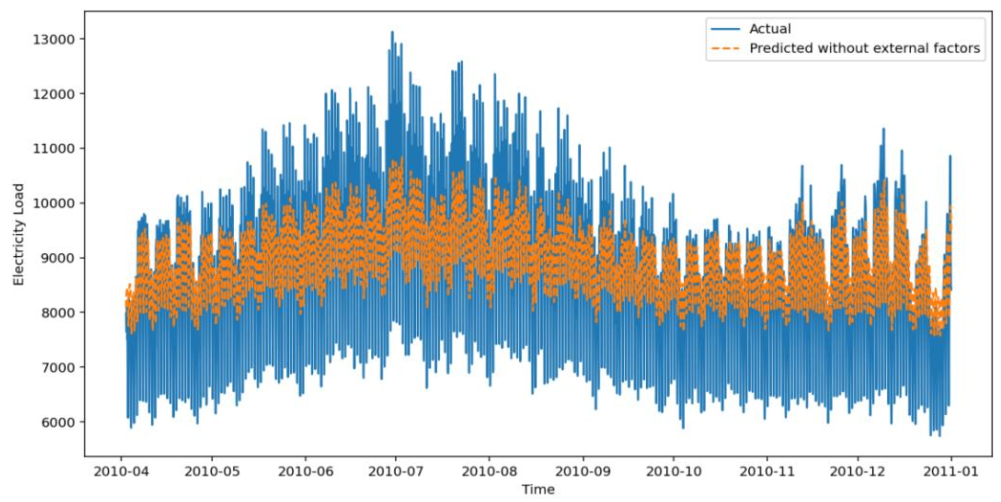
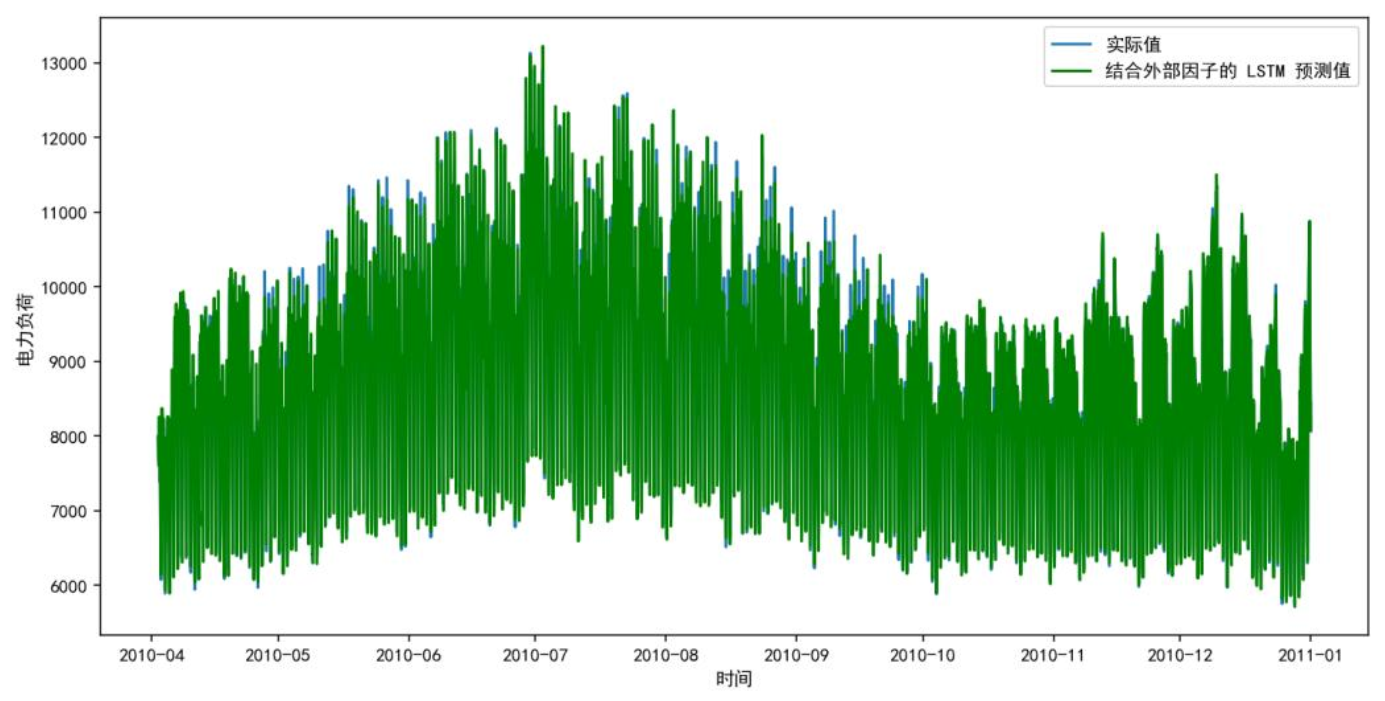
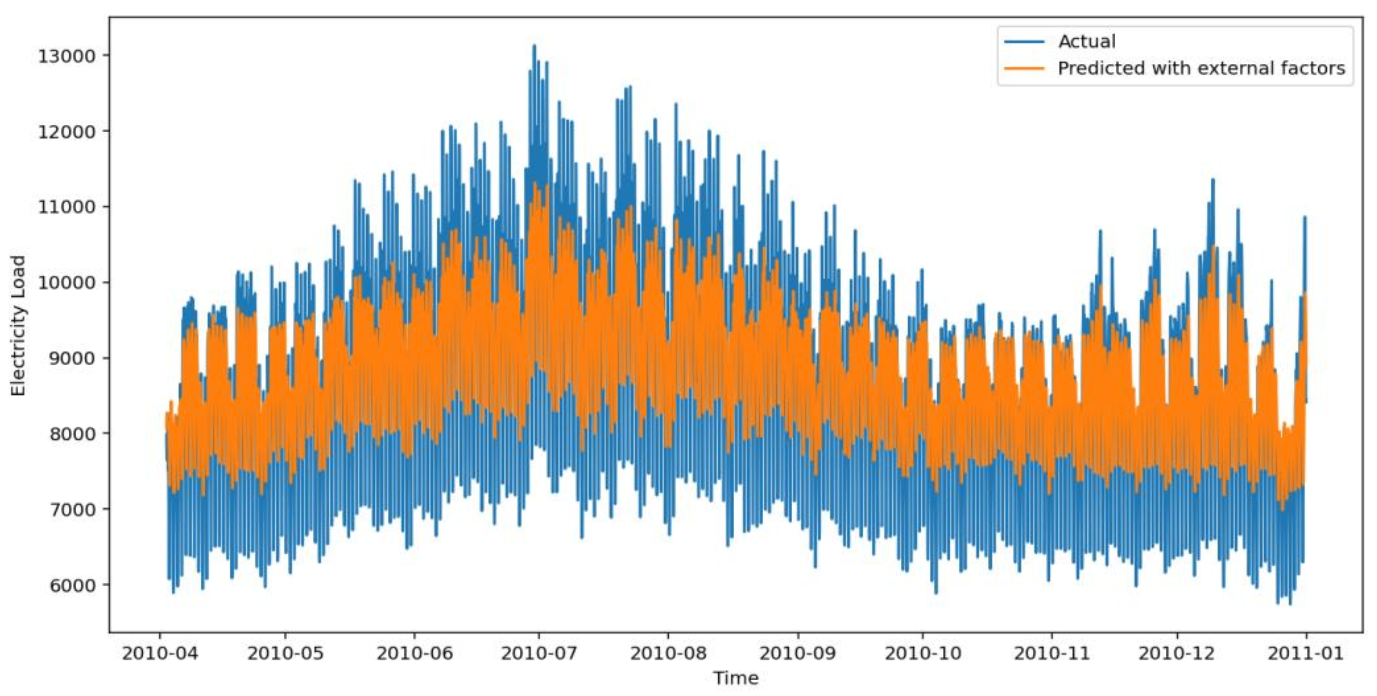
下图为变量与负荷的散点拟合图，温度呈“U型”（低温供暖、高温制冷推高负荷），湿度负相关（湿度升高负荷下降），电价低区间弹性高、高区间刚性强，验证多因子与负荷的非线性关联。 通过SHAP值量化因子对模型的影响，下图为变量指标SHAP值图，电价SHAP值范围广（-3000至1000），高值（红色）对应负荷降低；干球温度SHAP值覆盖广，证明其对模型影响关键；湿度SHAP值以负值为主，高湿度抑制负荷，与散点图结论一致。 将温度、湿度、电价融入基础模型，LSTM、GRU、DeepAR精度均有提升。下图为外部因子LSTM模型预测图，曲线贴合度大幅提高，2010年7月等波动时段预测偏差显著减小。 下图为外部因子DeepAR模型预测图，虽较基础模型提升，但仍逊于LSTM，波动时段把握不够精准。 下图为外部因子GRU模型预测图，常规场景拟合好，但电价突变+极端天气时精度受影响。

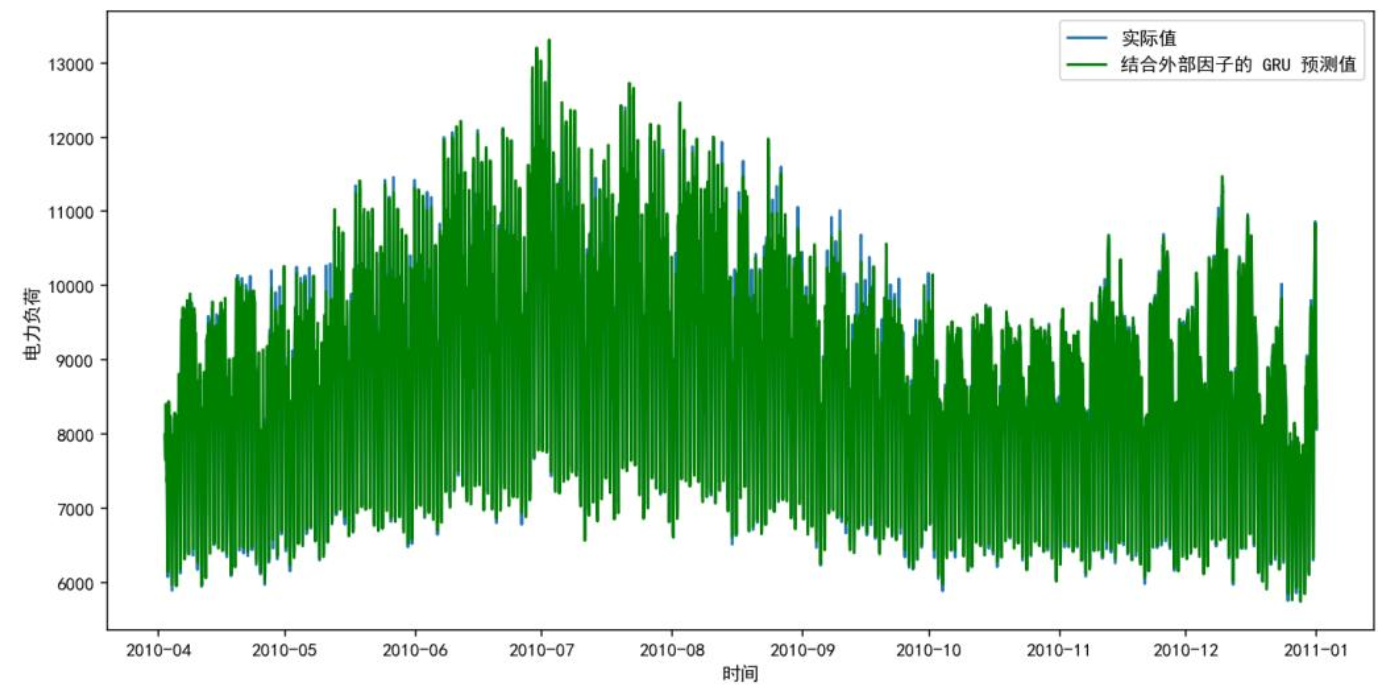
三种模型融入外部因子后的精度提升如下表，GRU降幅最显著（MAE降幅20.08%），LSTM综合最优（R²=0.9881）。

模型	MAE降幅	RMSE降幅	MAPE降幅	R²提升
外部因子LSTM	16.53%	16.10%	16.08%	0.0050
外部因子GRU	20.08%	26.00%	18.79%	0.0094
外部因子DeepAR	11.32%	11.66%	1.25%	0.1616

采用方差倒数法、XGBoost、Stacking三种方式组合模型，XGBoost组合效果最优，DeepAR-LSTM组合MAE=67.45、MAPE=0.7768%、R²=0.9951。下图为组合模型残差分布箱线图，可见DeepAR-LSTM残差中位数接近0、分布紧凑，鲁棒性最佳。 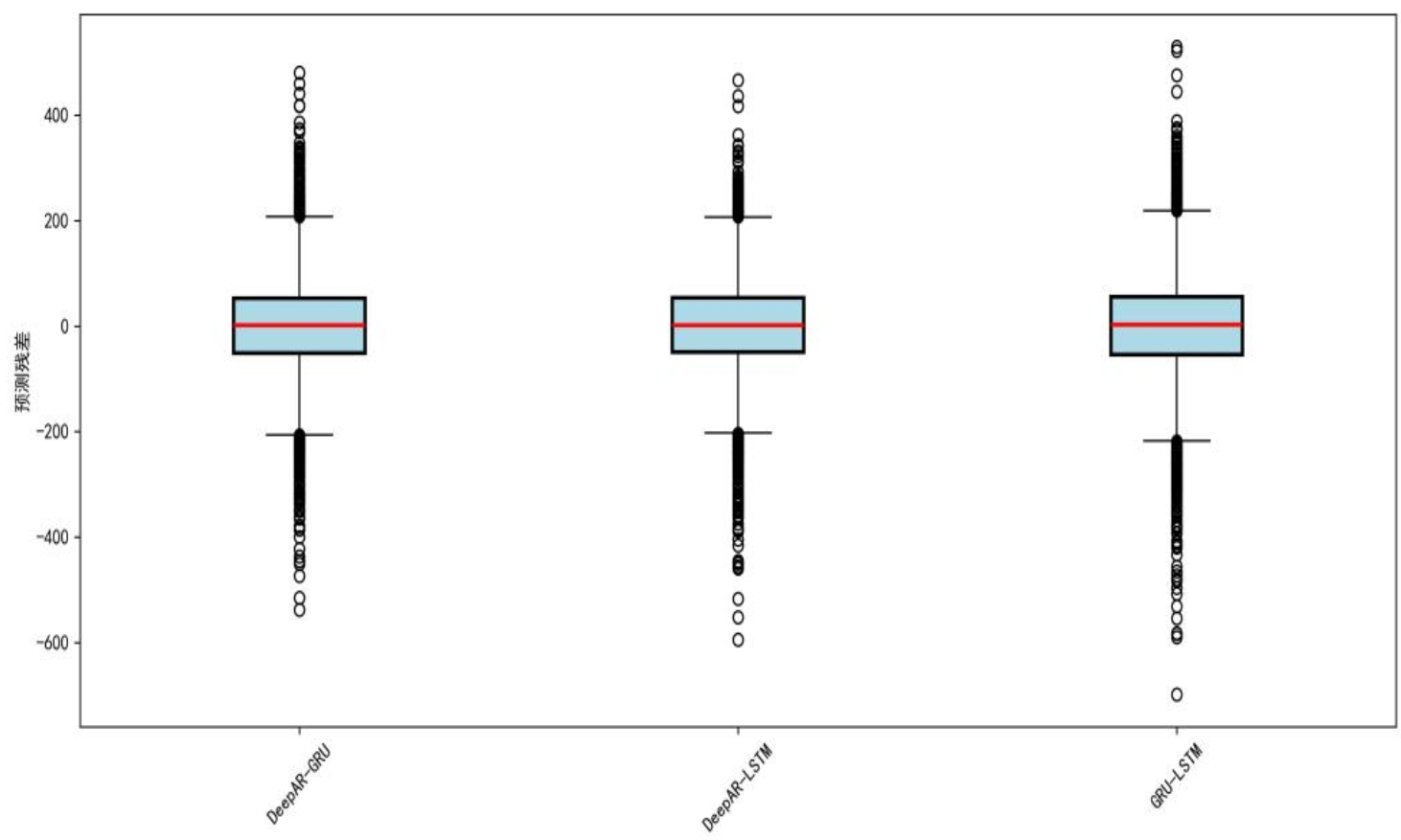通过SHAP分析各基础模型在组合中的作用：DeepAR-GRU组合中，GRU捕捉短期突变，DeepAR提供概率基准；DeepAR-LSTM组合中，LSTM挖掘长期趋势，DeepAR校准预测分布；LSTM-GRU组合中，两者形成长短时序互补。

针对学生在使用本文代码时可能遇到的“运行异常、查重风险、逻辑不懂”问题，我们提供： 1. 24小时应急修复：响应代码报错求助，比学生自行调试效率提升40%，例如模型训练报“维度不匹配”时，可快速定位特征拼接逻辑问题； 2. 人工拆解服务：讲解模型逻辑与代码适配思路，比如解释“为何LSTM需将2D特征转为3D”； 3. 原创保障：代码人工创作比例超90%，规避查重与漏洞风险，真正实现“买代码不如买明白”。

结论

本研究通过多源数据融合、深度学习与集成方法，解决了电力负荷预测的核心痛点： 1. 多源融合突破局限：温度、湿度、电价的引入使模型精度提升16%-26%，揭示气象-电价-负荷的非线性关联； 2. 集成模型最优适配：XGBoost组合模型实现精度与鲁棒性平衡，DeepAR-LSTM组合MAPE降至0.77%以下，满足国家电网调度1%精度要求； 3. 可解释性支撑决策：SHAP分析量化因子与基模型贡献，避免“黑箱”风险； 4. 地区场景精准适配：基于气候特征推荐模型，确保在不同城市落地实用。后续可融合新能源出力数据，提升高比例新能源消纳场景预测全面性。

参考文献

[1] 康重庆, 夏清. 电力系统负荷预测研究综述与发展方向的探讨[J]. 电力系统自动化, 2004(17): 1-11.
[2] 周明, 李庚银. 深度学习在电力系统中的应用综述[J]. 电网技术, 2018, 42(10): 3380-3390.
[3] 张东霞, 苗新. 人工智能在电力系统及综合能源系统中的应用[J]. 电力系统自动化, 2019, 43(1): 2-14.
[4] Salinas D, et al. DeepAR: Probabilistic forecasting with autoregressive recurrent networks[J]. International Journal of Forecasting, 2020, 36(3): 1181-1191.