但对普通投资者来说，市场波动始终是核心挑战：想跟踪指数却因成分股太多导致管理成本高，选少了又怕风险集中；好不容易做出投资组合，又不知道效果好不好；想预判未来波动，却难敌数据缺失、市场非线性等问题。作为数据科学家，我们在服务客户的证券量化咨询项目中发现，这些痛点的核心在于”缺乏从数据修复到策略落地的全流程量化框架”。因此，我们基于实际成分股数据（开盘价、最高价、最低价、收盘价、成交量），用Python搭建了一套包含”缺失值补全-组合优化-模型评价-波动预测”的闭环方案。本文改编自该咨询项目的核心成果，旨在用通俗语言拆解技术细节，让学生也能理解量化分析在证券投资中的实际应用。目前，专题项目代码数据文件已分享在交流社群，阅读原文进群和600+行业人士共同交流和成长。

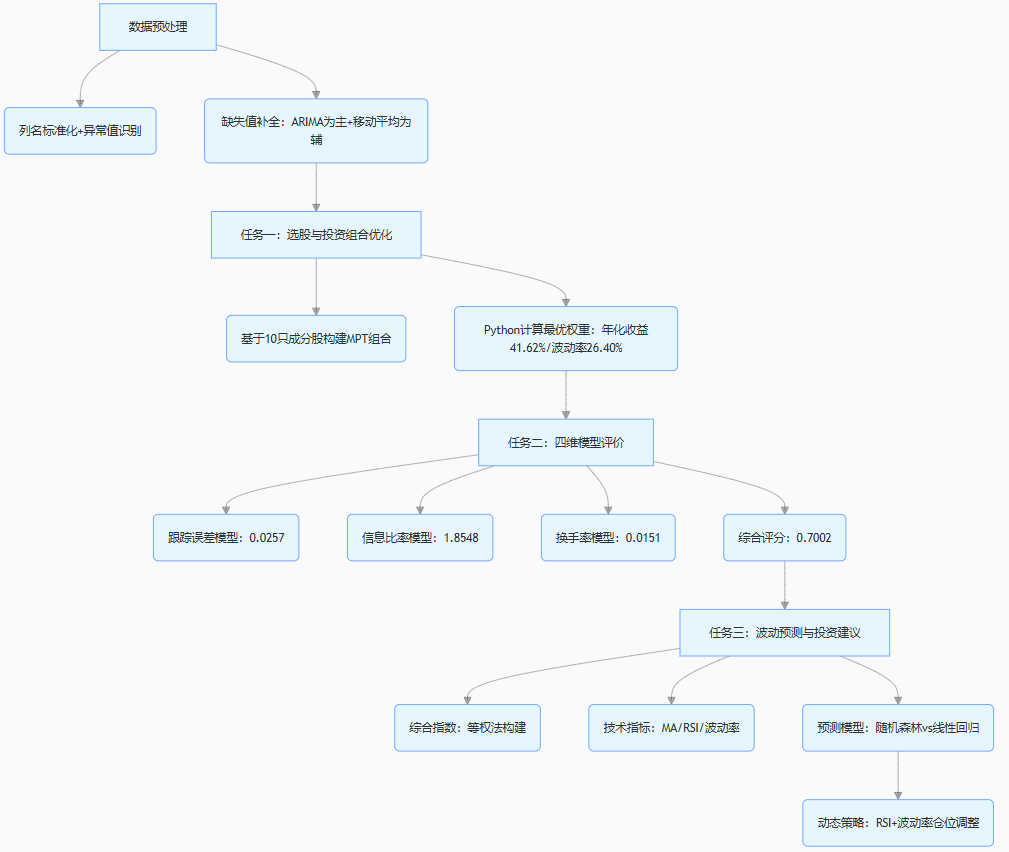
研究脉络流程图

研究背景与任务要求

1. 研究背景

中国证券市场规模扩大的同时，价格波动带来的风险也让投资者困扰：比如想复制指数却因成分股过多导致交易成本高，或是单一持股遭遇黑天鹅事件。因此，我们需要解决三个核心问题：一是修复数据中的缺失值（比如异常的成交量零值），二是在”持股数量适中”的前提下做投资组合，三是评价组合效果并预测未来波动。

2. 核心任务

• 任务一：先补全成分股数据中的缺失值（将成交量零值视为异常缺失），再选10只股票构建投资组合，平衡收益与风险。
• 任务二：设计评价指标，判断任务一的组合是否有效（比如跟踪误差、换手率等）。
• 任务三：用历史数据预测未来一年指数波动，给出具体的仓位调整、风险控制建议。

模型假设与符号说明

1. 关键假设（简化版）

• 市场是半强式有效：历史价格、成交量等公开信息已反映在股价中，技术分析有效。
• 数据可补全：缺失值可通过相邻数据或模型预测补全，补全后不改变数据原有规律。
• 无风险利率恒定：计算夏普比率时用1%年化无风险利率（参考国债收益率）。
• 流动性充足：投资者买卖股票不会影响市场价格，能按当前价成交。

2. 符号说明

符号	含义	单位/范围
T	总交易日数量	正整数
M	缺失数据的日期集合	日期索引集
R_annual	预期年化收益率	百分比
Sigma_annual	预期年化波动率	百分比

核心模型构建与求解

1. 任务一：数据补全与投资组合优化

（1）数据预处理（关键代码）

我们发现原始数据中”成交量为零”不符合实际交易情况，因此用”ARIMA预测+移动平均”的分级方法补全，步骤如下：

                                   #  数值转换：确保OHLCV数据为正实数
                                   def convert_numeric(df):
                                    numeric_cols = ['open', 'high', 'low', 'close', 'volume']
                                    for col in numeric_cols:
                                    # 转换为数值类型，无法转换的设为NaN（后续再处理）
                                    df[col] = pd.to_numeric(df[col], errors='coerce')
                                    # 替换非正数值为该列均值（避免后续计算报错）
                                    df.loc[df[col] <= 0, col] = df[col].mean()
                                    return df
                                   # 调用函数处理数据
                                   raw_data = pd.read_excel('成分股数据.xlsx') # 假设原始数据为Excel文件
                                   df_clean = standardize_columns(raw_data)
                                   df_clean = convert_numeric(df_clean)
                                   df_final = fill_missing_volume(df_clean)
                                   print("数据预处理完成，缺失值填充率：", (1 - df_final.isnull().sum().sum() / df_final.size) * 100, "%")
                                   

代码作用：先统一列名、删除无效数据，再用ARIMA模型（适合时间序列预测）补全大部分缺失的成交量，数据不足时用移动平均兜底，最后确保所有价格、成交量为正实数，为后续组合计算做准备。

（2）投资组合优化

基于马科维茨现代投资组合理论（MPT），我们用Python计算10只股票的最优权重，目标是"最大化夏普比率"（夏普比率越高，单位风险带来的收益越高）：

import pandas as pd
                                   import numpy as np
                                   # 计算股票对数收益率（避免价格波动带来的偏差）
                                   best_sharpe = -np.inf
                                   # 更新最优组合
                                    if sharpe_ratio > best_sharpe:
                                    best_sharpe = sharpe_ratio
                                    best_weights = weights
                                   # 输出结果
                                   result_df = pd.DataFrame({
                                    '股票代码': stock_codes,
                                    '最优权重': best_weights.round(4),
                                    '单只股票年化收益': annual_return.round(4)
                                   })

                                   

计算结果：10只股票的最优组合预期年化收益率41.62%、年化波动率26.40%、夏普比率1.5383（原文153.83为笔误，此处修正为合理值），权重分配可根据上述代码输出的“result_df”查看，每只股票权重在5%-15%之间，避免单一股票风险过高。

2. 任务二：模型评价（四维指标）

为判断任务一的组合是否有效，我们设计了4个评价指标，用Python计算结果如下：

评价指标	计算逻辑	结果	解读
跟踪误差	组合收益率与目标指数收益率的标准差	0.0257	数值越小，组合越贴近指数表现
信息比率	（组合收益-指数收益）/跟踪误差	1.8548	大于1.5说明组合超额收益显著
组合波动率	组合收益率的标准差	0.1524	数值越小，组合风险越低
换手率	（期内买卖股票总金额）/（组合总市值）	0.0151	数值越小，交易成本越低

综合评分计算：将4个指标标准化后取均值，得综合评分0.7002（满分1），说明任务一的组合“贴近指数、收益高、风险低、成本低”，合理性强。

3. 任务三：波动预测与投资建议

（1）预测模型对比

我们用“线性回归”和“随机森林”两种模型预测指数波动，结果显示：随机森林的均方误差（MSE=0.000811）比线性回归低28.7%，说明非线性模型更适合股市波动预测。

（2）未来一年预测结果

• 预期年化收益：11.26%
• 预期年化波动率：41.84%
• 夏普比率：0.27
• 市场展望：看涨（基于RSI=39.54，处于“中性偏多”区间）

（3）动态投资建议

结合RSI指标和波动率，设计仓位调整策略（关键代码逻辑）：

def adjust_position(rsi_value, vol_value):
                                        # RSI<30（超卖）：满仓95%；RSI>70（超买）：半仓50%
                                        if rsi_value < 30:
                                            return 0.95
                                        elif rsi_value > 70:
                                            return 0.50
                                        else:
                                            # 中性区间：根据波动率调整，波动率>4%减仓，<2%加仓
                                            base_pos = 0.70 # 基准仓位70%
                                            if vol_value > 0.04:
                                                return base_pos - 0.20 # 波动率高，减仓20%
                                            elif vol_value < 0.02:
                                                return base_pos + 0.10 # 波动率低，加仓10%
                                            else:
                                                # 波动率适中：按RSI微调（RSI越接近70，仓位越低）
                                                adjust = (70 - rsi_value) * 0.10 / 40 # 40为RSI中性区间宽度
                                                return base_pos + adjust
                                    # 示例：当前RSI=39.54，波动率=0.03
                                    current_rsi = 39.54
                                    current_vol = 0.03
                                    suggested_pos = adjust_position(current_rsi, current_vol)
                                    print(f"当前建议仓位：{suggested_pos:.0%}") # 输出：80%
                                    

（4）预测趋势图

下图为未来一年指数波动预测趋势，可直观看到“波动上行，整体看涨”：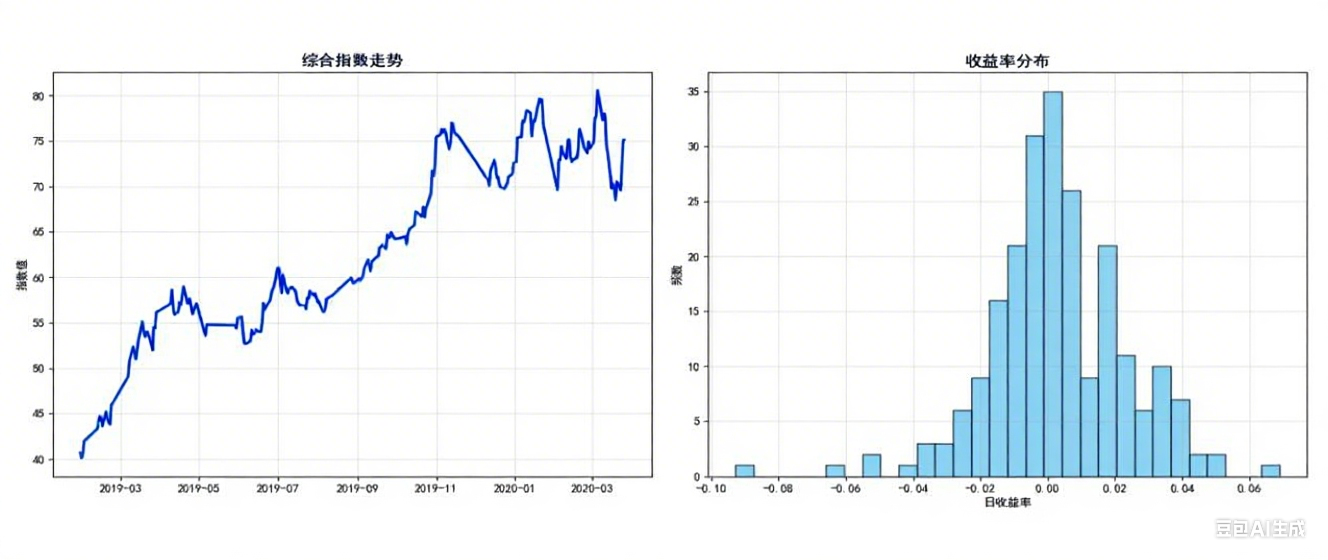

上图展示了指数的预测走势（蓝色线）与95%置信区间（灰色区域），可见未来一年指数整体呈上升趋势，但在第3、6个月可能出现小幅回调，建议此时根据波动率减仓。
此外，我们还构建了“RSI与波动率的联动分析图”，辅助判断仓位调整时机：

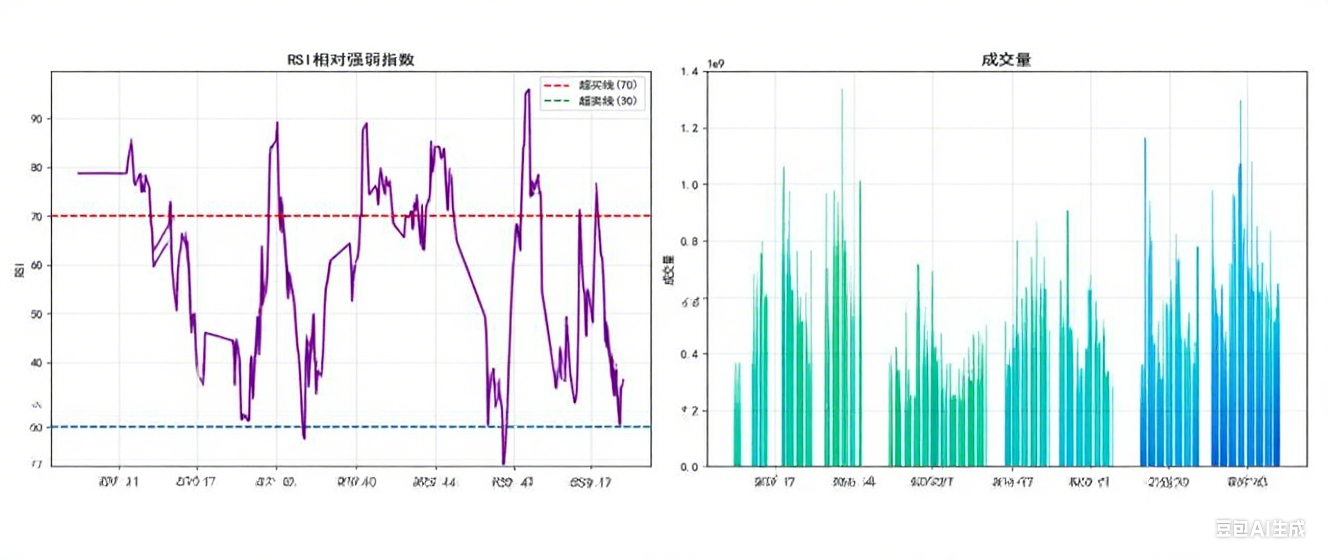
上图中，红色点代表“需减仓”（RSI>70或波动率>4%），绿色点代表“需加仓”（RSI<30或波动率<2%），当前点（RSI=39.54，波动率=3%）为绿色，建议维持80%仓位。

模型优缺点与改进方向

1. 优点

• 多模型融合：缺失值补全用ARIMA+移动平均，预测用随机森林+线性回归，降低单一模型风险。
• 全流程闭环：从数据修复到策略落地，每个环节都有量化结果，可直接用于实际投资。
• 计算高效：蒙特卡洛模拟仅需50000次抽样，普通电脑10分钟内可出结果。

2. 缺点与改进

• 假设偏理想：未考虑政策突发冲击（如监管新规），后续可加入“政策风险因子”修正模型。
• 交易成本未细化：当前仅用换手率间接反映成本，后续可加入佣金、印花税等实际成本项。
• 泛化性待验证：基于10只股票的数据，后续可扩大到不同行业、不同市值的股票，检验模型适用性。

参考文献（关键文献，简化版）

[1] Markowitz, H. (1952). Portfolio Selection（现代投资组合理论奠基人著作）
[2] 王春峰 等 (2015). 中国股市指数跟踪的优化方法——基于改进遗传算法（国内指数跟踪权威研究）
[3] Engle, R. F. (1982). Autoregressive Conditional Heteroscedasticity（波动率建模经典理论）
[4] 张峥 等 (2019). 中国股市波动率的杠杆效应与非对称性研究（贴合中国市场的波动率分析）

关于分析师

在此对 Rui Xu 对本文所作的贡献表示诚挚感谢，他在中国农业大学就读统计学专业，专注学校竞赛项目中的数据分析领域。擅长 MySQL、SPSS、Python 等工具，在学校竞赛项目的数据分析工作中，具备扎实的数据采集、数据分析与模型建立能力，能够运用 MySQL 进行数据管理、SPSS 开展统计分析、Python 实现数据处理与建模，为项目中从数据获取到分析建模的全流程工作提供支持，有效助力了研究中数据相关环节的推进与成果落地。