
贝叶斯隐马尔可夫模型是一种用于分割连续多变量数据的概率模型。
该模型将数据解释为一系列隐藏状态生成。每个状态都是重尾分布的有限混合,具有特定于状态的混合比例和共享的位置/分散参数。
可下载资源
该模型中的所有参数都配备有共轭先验分布,并通过变化的贝叶斯(vB)推理算法学习,其本质上与期望最大化相似。该算法对异常值具有鲁棒性,并且可以接受缺失值。
隐马尔可夫模型(Hidden Markov model, HMM)是一种结构最简单的动态贝叶斯网的生成模型,它也是一种著名的有向图模型。它是典型的自然语言中处理标注问题的统计机器学模型,本文将重点介绍这种经典的机器学习模型。
一、引言
假设有三个不同的骰子(6面、4面、8面),每次先从三个骰子里面选择一个,每个骰子选中的概率为1/3,如下图所示,重复上述过程,得到一串数值[1,6,3,5,2,7]。这些可观测变量组成可观测状态链。同时,在隐马尔可夫模型中还有一条由隐变量组成的隐含状态链,在本例中即骰子的序列。比如得到这串数字骰子的序列可能为[D6, D8, D8, D6, D4, D8]。
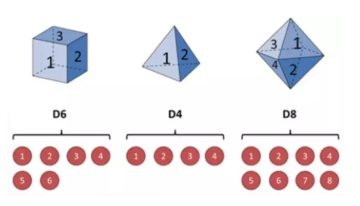
隐马尔可夫型示意图如下所示:
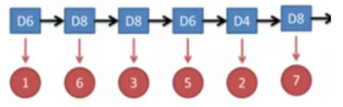
图中,箭头表示变量之间的依赖关系。图中各箭头的说明如下:
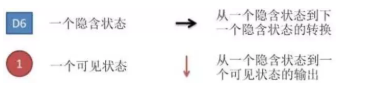
在任意时刻,观测变量(骰子)仅依赖于状态变量(哪类骰子),同时t时刻的状态qt仅依赖于t-1时刻的状态qt-1。这就是马尔科夫链,即系统的下一时刻仅由当前状态(无记忆),即“齐次马尔可夫性假设”
二、隐马尔可夫模型的定义
根据上面的例子,这里给出隐马尔可夫的定义。隐马尔科夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个可观测的随机序列的过程,隐藏的马尔可夫链随机生成的状态序列,称为状态序列(也就上面例子中的D6,D8等);每个状态生成一个观测,而由此产生的观测随机序列,称为观测序列(也就上面例子中的1,6等)。序列的每个位置又可以看作是一个时刻。
隐马尔可夫模型由初始的概率分布、状态转移概率分布以及观测概率分布确定。具体的形式如下,这里设Q是所有可能的状态的集合,V是所有可能的观测的集合,即有:
![]()
其中,N是可能的状态数,M是可能观测的数。另外设I是长度为T的状态序列,O是对应的观测序列:
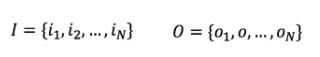
在马尔可夫链中,有几个矩阵变量,分别是状态转移概率矩阵A,观测概率矩阵B,以及初始状态概率向量C,其中状态转移概率矩阵A为:
![]()
其中,
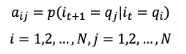
是在时刻t处于状态qi的条件下生成状态qj的概率。
初始状态概率向量为:
![]()
Ci为时刻t=1处于状态qi的概率。
隐马尔可夫模型由初始状态概率向量C,状态转移概率矩阵A和观测概率矩阵B决定,C和A决定状态序列,B决定观测序列,因此隐马尔可夫模型可以用三元符号表示为:
![]()
A、B和C也被称为隐马尔科夫模型的三要素。
状态转移概率矩阵A与初始状态概率向量C确定了隐藏的马尔可夫链,生成不可观测的状态序列,观测概率矩阵B确定了如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
从定义中,可以发现隐马尔可夫模型作了两个基本假设:
(1) 马尔可夫性假设,即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其它时刻的状态及观测无关,也与时刻t无关,
![]()
(2) 观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
![]()
隐马尔可夫模型可以用于标注,这时状态对应着标记,标注问题是给定观测的序列预测其对应的标记序列。可以假设标注问题的数据是由隐马尔可夫模型生成的,这样可以利用该模型的学习与预测算法进行标注。
隐马尔科夫模型的三个基本问题:
(1) 概率计算问题:给定模型lamda=(A,B,C)和观测序列O=(o1,o2,…,oT),计算在该模型下观测序列O出现的概率P(O|lamda)。
(2) 学习问题:一直观测序列O=(o1,o2,…,oT),估计模型lamda=(A,B,C)参数,使得在该模型下观测序列概率P(O|lamda)最大,即用极大似然估计的方法估计参数。
(3) 预测问题,也称为解码的问题,已知模型lamda=(A,B,C)和观测序列O=(o1,o2,…,oT),求对给定观测序列条件概率P(I|O)最大的状态序列 I = (i1,i2,…,iT),即给定观测序列,求最有可能的对应的状态序列。
三、前向算法
在介绍前向算法之前,先介绍前向概率。
前向概率:在给定隐马尔科夫模型lamda,定义到时刻t部分观测序列为o1,o2,…,ot且状态为qi的概率为前向概率,记为:
![]()
可以根据数据对前向概率公式进行递推,并最终得到观测序列概率P(O|lamda). 前向概率算法就是根据前向概率递推公式进行计算的,输入为隐马尔可夫模型和观测序列,输出的结果为序列概率P(O|lamda). 计算的步骤为:
(1) 根据前向概率公式,先设定 t = 1的初值:
![]()
(2) 根据前向概率公式对前向概率进行递推,因此对t=1,2,…,N-1有:
![]()
(3) 最后对所有的前向概率进行求和得到最终的结果,即为:
![]()
该算法所表示的递推关系图为:
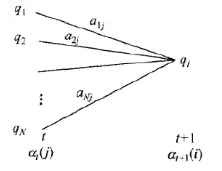
对于步骤一的初始,是初始时刻的状态i1 = q1和观测o1的联合概率。步骤(2) 是前向概率的递推公式,计算到时刻t+1部分观测序列为o1,o2,…,ot,ot+1 且在时刻t+1处于状态qi的前向概率。如上图所示,既然at(j)是得到时刻t观测到o1,o2,…,ot并在时刻t处于状态的qj前向概率,那么at(j)aji就是到时刻t观测到o1,o2,…,ot并在是时刻t处于qj状态而在时刻t+1到达qi状态的联合概率。对于这个乘积在时刻t的所有可能的N个状态求和,其结果就是到时刻t观测为o1,o2,…,ot,并在时刻t+1处于状态qi的联合概率。最后第三步,计算出P(O|lamda)的结果。
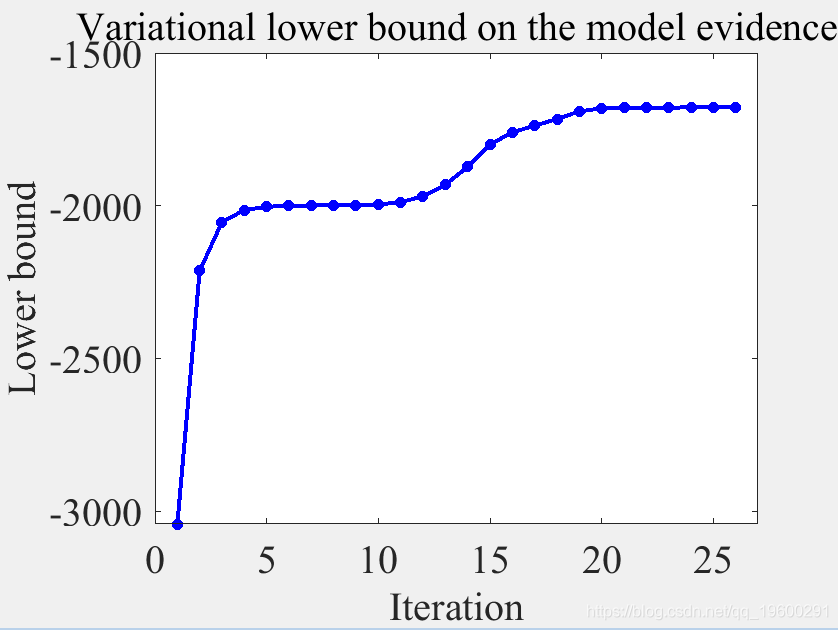
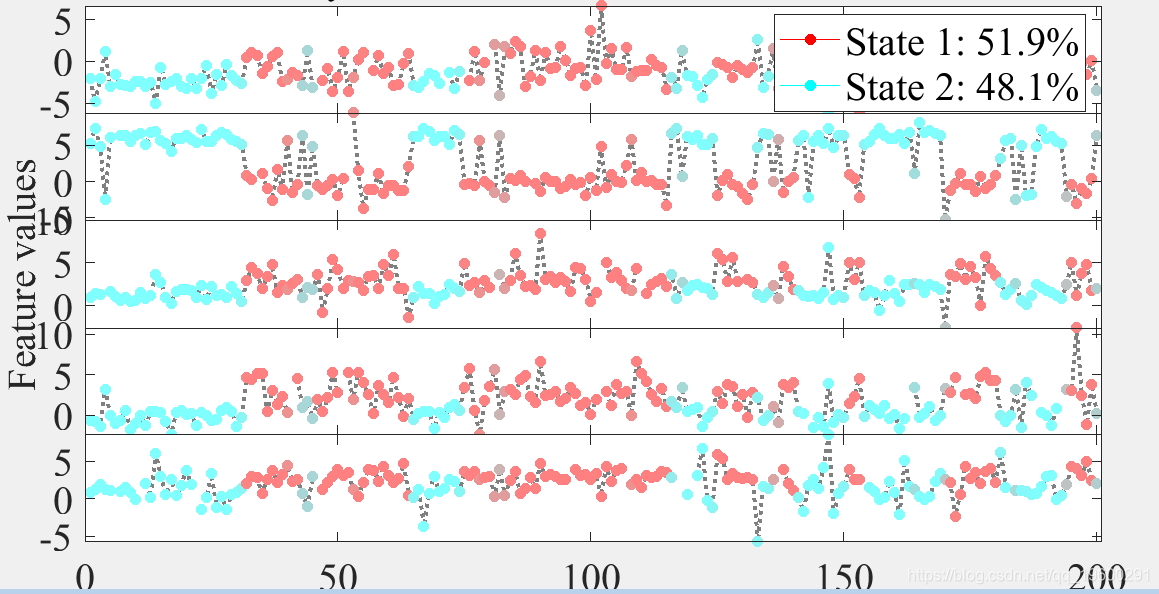
本文从未知的BRHMM生成一组数据序列 参数,并仅从这些数据中估算出 生成它们的模型。 结果绘制为 时间序列
设置状态,符号和特征的数量
NumState=2;
NumSym=3;
NumFeat=5;设置序列数,每个序列点数和缺失值
NumSeq=2;
NumPoint=100;
NumMiss=20;设置参数生成选项。TransParam=1/5
EmissParam=1/5;
LocParam=2;
DispParam=5;设置采样选项
NumDeg=5;
NumObs=1000;输出和显示状态
fprintf('\n')
fprintf('Sampling data ... ')生成用于采样的参数
[Trans,Emiss,Loc,Disp]=GenParam(NumState,NumSym,NumFeat,...
TransParam,EmissParam,LocParam,DispParam);

创建用于采样的模型
Obj= bhnn(NumState,NumSym,NumFeat);
设置超参数
Obj.TransWeight=Trans;
Obj.TransStren(:)=NumObs;
Obj.EmissWeight=Emiss;
Obj.EmissStren(:)=NumObs;
Obj.CompLoc=Loc;
Obj.CompScale(:)=NumObs;
Obj.CompDisp=Disp;
Obj.CompPrec(:)=max(NumObs,NumFeat);采样数据并随机删除值
更新状态
fprintf('Done\n')
fprintf('Estimating model ... ')创建估计模型
Obj=BHMM(NumState,NumSym,NumFeat);
约束过渡参数
Obj.TransWeight=Trans;
Obj.TransStren(:)=NumObs;随时关注您喜欢的主题
估计模型和状态概率
更新状态

绘制结果

更新状态
% 更新状态
fprintf('Done\n')
fprintf('\n')
end


 Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程
Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用



