本示例说明如何创建并可视化Markov链模型的结构和演化 。
创建实际GDP的马尔可夫链模型。指定状态名称。
马尔可夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。举个形象的比喻，假如每天的天气是一个状态的话，那个今天是不是晴天只依赖于昨天的天气，而和前天的天气没有任何关系。当然这么说可能有些武断，但是这样做可以大大简化模型的复杂度，因此马尔可夫链在很多时间序列模型中得到广泛的应用，比如循环神经网络RNN，隐式马尔可夫模型HMM等，当然MCMC也需要它。
如果用精确的数学定义来描述，则假设我们的序列状态是
，那么我们的在时刻 的状态的条件概率仅仅依赖于时刻
，即：
既然某一时刻状态转移的概率只依赖于它的前一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。
P = [0.5 0.5 0.0 0.0;
0.5 0.0 0.5 0.0;
0.0 0.0 0.0 1.0;
0.0 0.0 1.0 0.0];
stateNames = ["Regime 1" "Regime 2" "Regime 3" "Regime 4"];
mc = mc(P,'StateNames'可视化马尔可夫链的一种方法是绘制转移矩阵的热图。
可视化马尔可夫链的一种方法是绘制转移矩阵的热图。
figure;
imagesc(P);
colormap(jet);
colorbar;
axis squar
有向图
有向图将链中的状态显示为节点，并将状态之间的可行转换显示为有向边。
绘制马尔可夫链的默认有向图。
figure;plot(mc);通过基于转移概率指定边缘颜色来比较转移概率。
figure;plot(mc,'ColorEdges'通过根据状态类型指定节点颜色和标记来识别循环状态和瞬态状态。
figure;h = hplot(mc,'ColorEdges',true,
低均值状态是瞬态的，最终转移到递归的高均值状态。
节点标签的默认字体大小为8。将字体大小减少到7。
FontSize = 7;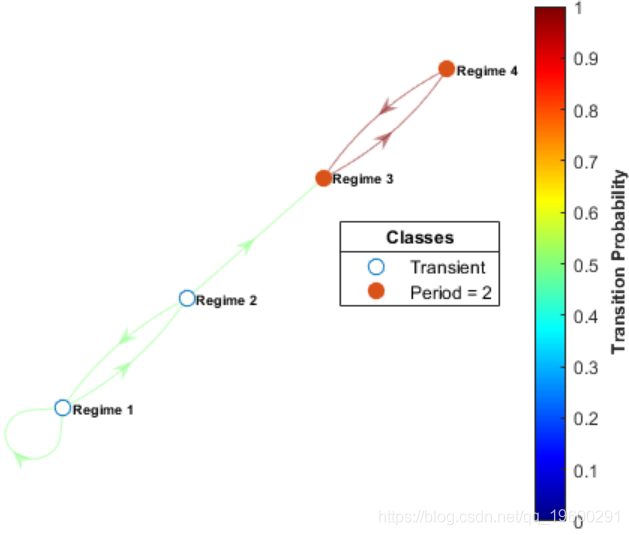
混合图
可以通过在有向图中绘制目标概率和预期的第一次命中时间来可视化。
从马尔可夫链中的每个状态开始计算命中目标状态的指定子集的概率。其中节点颜色表示命中概率。
绘制马尔可夫链的有向图，其中节点颜色表示命中方案1的概率。
htp(mc,"Regime 1",'Graph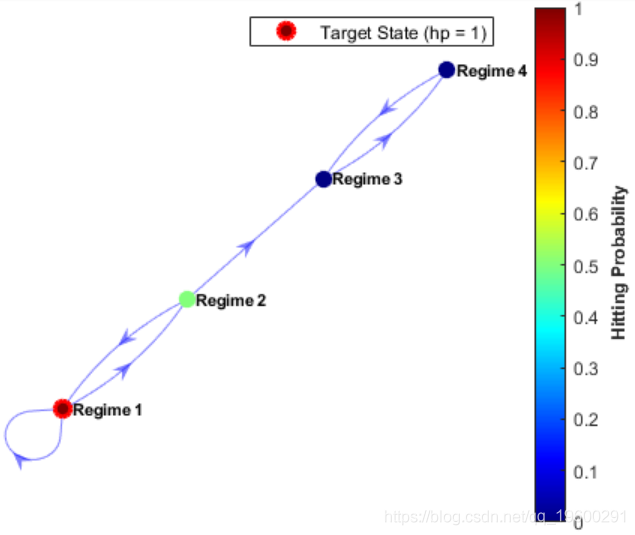
从马尔可夫链中的每个状态开始，计算目标状态的指定子集的预期首次命中时间。其中节点颜色表示命中时间。
绘制马尔可夫链的有向图，其节点颜色表示包含状态3和4的目标子类的预期首次命中时间。
target = ["Regime 3" "Regime 4"];htime(mc,target从方案1开始，该子类的预期首次命中时间为6个时间步长。
特征值图
特征值图显示了复平面上的特征值。特征值图并标识：
- Perron-Frobenius特征值，使用粗体星号为非负矩阵。
- 光谱间隙，即长度等于第二大特征值幅度（SLEM）的半径和长度为1的半径之间的区域。光谱间隙决定了马尔可夫链的混合时间。大间隙表示混合较快，而细间隙表示混合较慢。
在复杂平面上绘制并返回转换矩阵的特征值。
figure;eigplt(mc)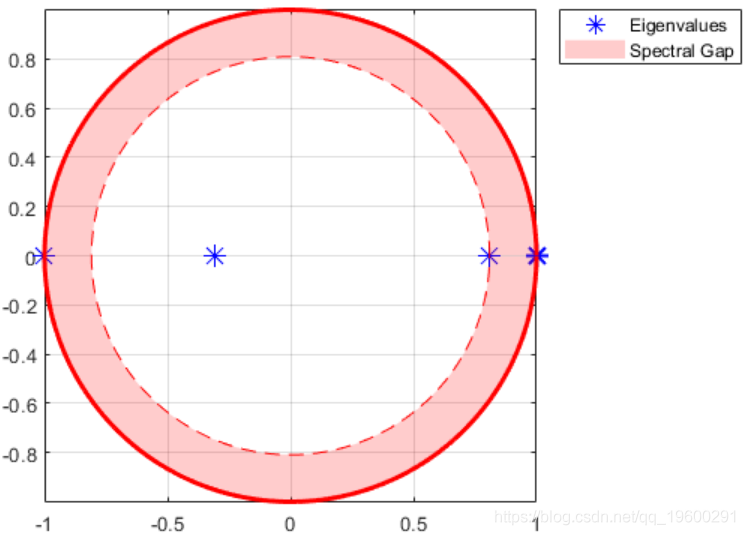
eVals = 4×1 0.8090 -0.3090 1.0000 -1.0000 两个特征值的模量为1，表明马尔可夫链的周期为2。
重新分配图
重新分布图从初始分布绘制了状态重新分布。 使用马尔可夫链对象生成的数据来绘制重新分布 。可以将重新分布绘制为静态热图或动画直方图或有向图。
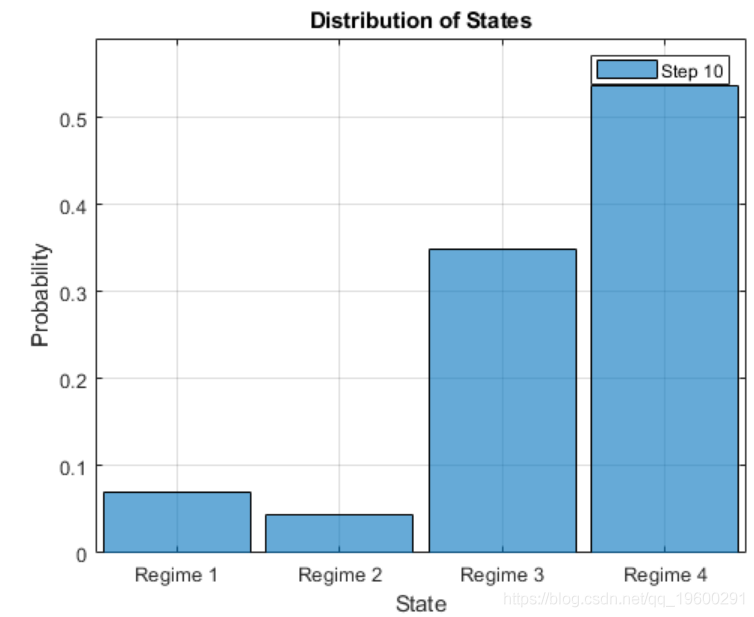
从初始分布生成10步重新分布。
redis(mc,numSteps,'X0',x0);将重新分布绘制为热图。
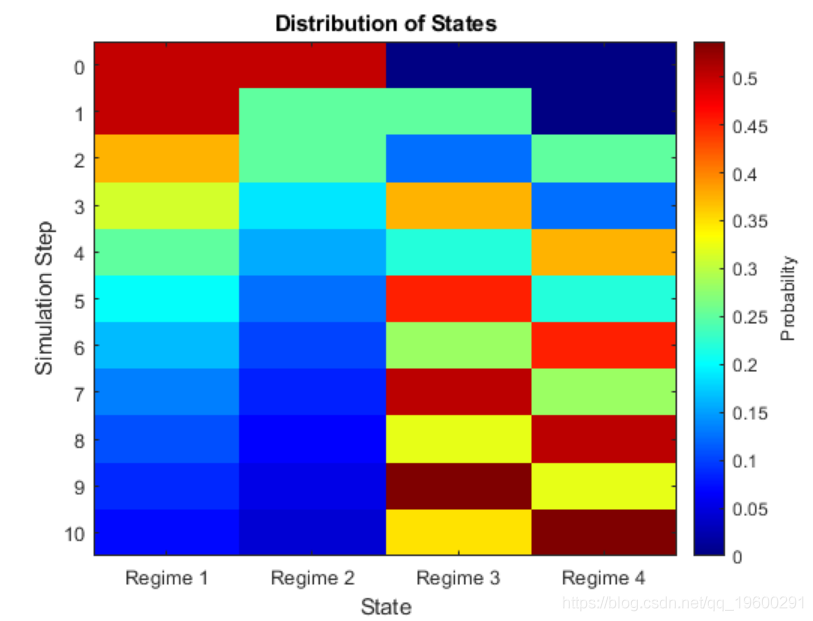
由于状态1和状态2是瞬态的，因此马尔可夫链最终将概率集中在状态3和状态4。此外，如特征值图所示，状态3和状态4的周期为2。
绘制动画直方图。将帧速率设置为一秒。
仿真图
仿真图绘制了从特定初始状态开始的马尔可夫链的随机游动图。
生成100个十步随机游走，其中每个状态都会初始化游走25次。
simu(mc,numSteps,将模拟绘制为热图，以显示每个步骤达到的状态比例。
绘制已实现转移矩阵的热图。
figure;simp(mc,X,'Type','transition');所实现的转移矩阵看起来类似于理论转移矩阵。
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
R语言SVM模型用大学生行为数据对助学金精准资助预测ROC可视化
R语言离散时间马尔可夫链（Markov chain）模型分类案例可视化分析
R语言《红楼梦》文本挖掘：词频统计、词云可视化及前后对比分析
