可下载资源

压缩技术很多，它们的用法和兼容性也各不相同。

压缩有两种主要类型：

• 无损：即使我们不太“精打细算”，数据完整性和准确性也是首选
• 有损：数据完整性和准确性并不像我们提供服务的速度那么重要-想象一下实时视频传输，其中“实时”传输比拥有高质量视频更为重要

当然，这是有损压缩的一个示例，因为我们已经丢失了很多信息。

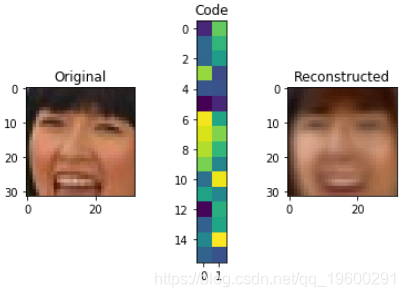
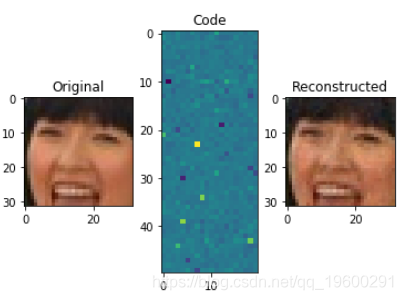
不过，我们可以使用完全相同的技术，通过为表示分配更多的空间来更精确地做到这一点：

def decode_image_from_raw_bytes(raw_bytes):
    img = cv2.imdecode(np.asarray(bytearray(raw_bytes), dtype=np.uint8), 1)
    img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    return img

另一个是实际加载数据集并使其适应我们的需求：

为了能够看到图像，让我们创建一个show_image函数。0.5由于像素值不能为负，它将添加到图像中：

现在，让我们快速浏览一下我们的数据：

show_image(X[6])

 现在让我们将数据分为训练和测试集：

sklearn train_test_split()函数能够通过给它测试比率来分割数据，其余的当然是训练量。的random_state，你会看到很多机器学习，用来产生相同的结果，不管你有多少次运行代码。

现在该模型了：

此函数将image_shape（图像尺寸）和code_size（输出表示的大小）作为参数。 

从逻辑上讲，该值越小code_size，图像将压缩得越多，但是保存的功能就越少，并且所复制的图像与原始图像的差异会更大。

由于网络体系结构不接受3D矩阵，因此该Flatten层的工作是将(32,32,3)矩阵展平为一维数组（3072）。

现在，将它们连接在一起并开始我们的模型：

 之后，我们通过Model使用inp和reconstruction参数创建一个链接它们，并使用adamax优化器和mse损失函数对其进行编译。

在这里编译模型意味着定义其目标以及达到目标的方式。在我们的上下文中，目标是最小化，mse并通过使用优化程序来达到此目的-从本质上讲，这是一种经过调整的算法，可以找到全局最小值。

 结果：

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
input_6 (InputLayer)         (None, 32, 32, 3)         0
_________________________________________________________________
sequential_3 (Sequential)    (None, 32)                98336
_________________________________________________________________
sequential_4 (Sequential)    (None, 32, 32, 3)         101376
=================================================================
Total params: 199,712
Trainable params: 199,712
Non-trainable params: 0
_________________________________________________________________

在这里我们可以看到输入是32,32,3。 

隐藏层是32  ，您看到的解码器输出是(32,32,3)。

 模型：

在本例中，我们将比较构造的图像和原始图像，因此x和y都等于X_train。理想情况下，输入等于输出。

该epochs变量定义多少次，我们要训练数据通过模型过去了，validation_data是我们用来评估训练后的模型验证组：

Train on 11828 samples, validate on 1315 samples
Epoch 1/20
11828/11828 [==============================] - 3s 272us/step - loss: 0.0128 - val_loss: 0.0087
Epoch 2/20
11828/11828 [==============================] - 3s 227us/step - loss: 0.0078 - val_loss: 0.0071
.
.
.
Epoch 20/20
11828/11828 [==============================] - 3s 237us/step - loss: 0.0067 - val_loss: 0.0066

我们可以将 损失可视化，以获得 概述。

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()

我们可以看到，在第三个时期之后，损失没有明显的进展。 

这也可能导致模型过度拟合，从而使其在训练和测试数据集之外的新数据上的表现不佳。

现在，最令人期待的部分-让我们可视化结果：

def visualize(img,encoder,decoder):
”“绘制原始，编码和解码的图像”“”
     ＃img [None]的形状为（1、32、32、3），与模型输入相同
    code = encoder.predict(img[None])[0]
    reco = decoder.predict(code[None])[0]
 
    plt.subplot(1,3,1)
    plt.title("Original")
    show_image(img)
 
    plt.subplot(1,3,2)
    plt.title("Code")
    plt.imshow(code.reshape([code.shape[-1]//2,-1]))
 
    plt.subplot(1,3,3)
    plt.title("Reconstructed")
    show_image(reco)
    plt.show()
 
for i in range(5):
    img = X_test[i]
    visualize(img,encoder,decoder)

 现在，让我们增加code_size至1000：

我们刚刚做的就是主成分分析（PCA），这是一种降维技术。我们可以通过生成较小的新功能来使用它来减小功能集的大小，但是仍然可以捕获重要信息。

主成分分析是 一种非常流行的用法。

图像去噪

 另一种流行用法是去噪。让我们在图片中添加一些随机噪声：

def apply_gaussian_noise(X, sigma=0.1):
    noise = np.random.normal(loc=0.0, scale=sigma, size=X.shape)
    return X + noise

在这里，我们从标准正态分布中添加了一些随机噪声，其大小为sigma，默认为0.1。

作为参考，这是具有不同sigma值的噪声的样子：

plt.subplot(1,4,1)
show_image(X_train[0])
plt.subplot(1,4,2)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.01)[0])
plt.subplot(1,4,3)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.1)[0])
plt.subplot(1,4,4)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.5)[0])

正如我们所看到的，几乎看不到图像的sigma增加0.5。我们将尝试从σ为的嘈杂图像中再生原始图像0.1。

我们将为此生成的模型与之前的模型相同，尽管我们将进行不同的训练。这次，我们将使用原始和相应的噪点图像对其进行训练：

现在让我们看一下模型结果：

结论

 主成分分析，这是一种降维技术，图像去噪等。