本文中我在R中构造一个简单的M / M / 1队列的_离散事件_模拟 。
像往常一样，我们从模拟及其检测所需的变量 开始。
模拟变量
t.end <- 10^5 # 模拟的持续时间 t.clock <- 0 # 模拟时间 Ta <- 1.3333 # 抵达间隔期 Ts <- 1.0000 # 服务期 t1 <- 0 # 下一次到达的时间 t2 <- t.end # 下一次出发的时间 tn <- t.clock # 最后事件时间的临时变量 tb <- 0 # 最后一次繁忙时间开始的临时变量 n <- 0 # 系统中的数量 s <- 0 # 累积数量-时间乘积 b <- 0 # 总忙碌时间 c <- 0 # 总完成数 qc <- 0 # 绘制瞬时q大小 tc <- 0 # 绘制时间延迟图 plotSamples <- 100 set.seed(1)
接下来，我们需要编写R代码以对进入队列和从队列离开进行实际的M / M / 1模拟。
仿真循环
============
while (t.clock < t.end) {
if(t1 < t2) { # 到达事件
t.clock <- t1
s <- s + n * (t.clock - tn) # 队列中的delta时间加权数
...
else {
t2 <- t.end
b <- b + t.clock - tb
}
}
}
检测指标
在这里，我们 检测数据以形成一些众所周知的性能指标。
队列长度
这是瞬时队列长度- 平均负载数据的曲线图。这就是排队波动的样子。
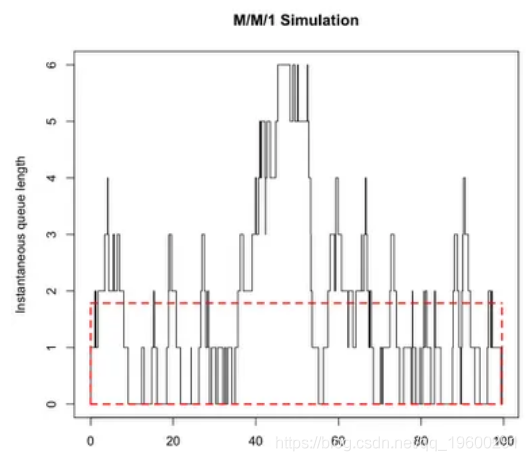
显示为红色虚线的框具有与阶梯曲线下方相同的面积。
PDQ模型
为了进行分析比较，我们还使用 PDQ-R模型。
是的，这几行代码与上面带工具的仿真代码等效，并且可以保证处于稳定状态。即使在R中运行PDQ本质上也是瞬时的。模拟将花费更长的时间，
随时关注您喜欢的主题
结果
最后，我们可以将模拟的M / M / 1队列与相应的PDQ结果进行比较。像往常一样，最好将它们分解为输入和输出。
- 输入：
Tsim：1.00e + 05 Ta：1.3333，Ts：1.0000＃次 Ar：0.7500，Sr：1.0000＃
- 输出：
Usim：0.7477，Updq：0.75 Xsim：0.7495，Xpdq：0.75 Rsim：4.0316，Rpdq：4.00 Qsim：3.0219，Qpdq：3.00
我们可以得出结论，仿真在指定的10 5个时间步长内达到了稳态。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
R语言布朗运动模拟股市、物种进化树状图、二项分布可视化
R语言收益率和波动性模拟股票价格COMP226带自测题
