
常用术语中的旅行推销员问题(TSP)是最复杂的问题之一,归结为组合优化。
旅行到n个城市(顶点)需要检查(n-1)!可能性。3,000个地点有4 * 10 ^ 9131个可能的解决方案。
本文调查了R包的性能:TSP和tspmeta。结果对我的使用非常满意。
以下代码输入您的TSP225.csv文件并输出您的解决方案和可视化。生成的’tour’对象是一类TOUR和整数;它包含您的解决方案。
coords.df <- data.frame(long=TSP225$Long, lat=TSP225$Lat)
coords.mx <- as.matrix(coords.df)
# Compute distance matrix
dist.mx <- dist(coords.mx)
# Construct a TSP object
tsp.ins <- tsp_instance(coords.mx, dist.mx )
#
tour <- run_solver(tsp.ins, method="2-opt")
#Plot
autoplot(tsp.ins, tour)
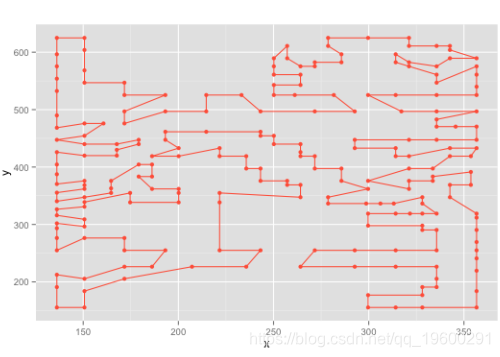

比较解决方案:下图显示了7种启发式解决方案的最佳旅游长度和协和式的确切解决方案。对于协和解决方案,我使用了在UW-Madison主持的NEOS-Server。
methods <- c("nearest_insertion" "2-opt")
tours <- sapply(methods simplify = FALSE)
dotchart( ),
)
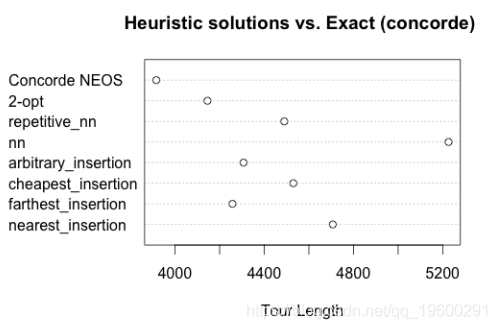
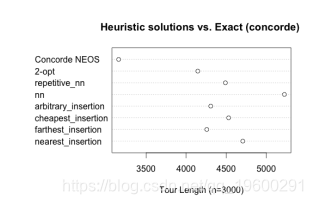
在2D中的#2 3000个随机顶点
显然,随着顶点数量的增长,精确解和其他启发式解决方案之间的差异显着增加。2-opt解决方案最接近最优。重复的2-opt解决方案和挑选最小的值让我非常接近于确切的解决方案 。



可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!





