
在本文中,我将介绍ARMA,ARIMA(Box-Jenkins),SARIMA和ARIMAX模型如何用于预测给定的时间序列数据。
我们可以使用backshift运算符来执行计算。例如,后轴运算符可用于计算的时间序列值的滞后差分y经由yi−Bk(yi),∀i∈k+1,…,t其中k表示的差分滞后期。
对于k=1,我们获得普通的成对差分,而对于k=2我们获得相对于一阶的差分。让我们考虑R中的一个例子。
使用R,我们可以使用diff函数计算滞后差分。函数的第二个参数表示所需的滞后k,默认设置为k=1。例如:
如何选择最优的模型
在讲具体模型之前,我们首先需知道什么是最优的模型,有怎样的标准去评价“最优”。通常来讲,akaike information criterion(AIC)和bayesian information criterion(BIC)是评价模型优良的两个指标。这两种评价指标不仅适用于事件序列模型,还广泛广泛运用于其他数学模型中。
AIC = -2 ln(L) + 2 k
BIC = -2 ln(L) + ln(n)*k
让我们来理解AIC的含义,AIC由两部分组成,一部分是对数极大似然函数,另一部分则是参数的个数。极大似然函数是评价模型拟合优劣性的指标,值越大说明拟合的效果越好。然而使用过多的参数可以拟合的很好却会出现过度拟合的情况,这样的模型泛化能力很差,因此加上参数的个数实际上是对极大似然函数进行”惩罚“。选取AIC值最小的模型作为最优模型,实质上是平衡了欠拟合和过拟合。
AR 模型
AR模型思想很简单,该模型认为通过时间序列过去时点的线性组合加上白噪声即可预测当前时点,它是随机游走的一个简单扩展。采用R可以去模拟一个简单的AR(1)序列:
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- 0.5*x[t-1] + w[t]
反过来可以采用MLE(极大似然法)估计参数和95%的置信区间:
x.ar <- ar(x, method = "mle")
x.ar$ar + c(-1.96, 1.96)*sqrt(x.ar$asy.var)
AR模型对偏自相关函数(PACF)截尾,对自相关函数(ACF)拖尾。所谓截尾指的是从某阶开始均为(接近)0的性质,拖尾指的是并不存在某一阶突然跳变到0而是逐渐衰减为0。
时间序列自相关与概率论中的相关定义本质是一致的,它衡量的是序列自身在不同时刻随机变量的相关性;偏自相关系数则剔除了两时刻之间其他随机变量的干扰,是更加纯粹的相关。
AR模型在金融模型中主要是对金融序列过去的表现进行建模,如交易中的动量与均值回归。
MA模型
MA模型和AR大同小异,它并非是历史时序值的线性组合而是历史白噪声的线性组合。与AR最大的不同之处在于,AR模型中历史白噪声的影响是间接影响当前预测值的(通过影响历史时序值)。
采用R可以去模拟一个简单的MA(1)序列:
x <- w <- rnorm(100)
for (t in 2:100) x[t] <- w[t] + 0.5*w[t-1]
同样可以去反过来估计MA的参数:
arima(x, order=c(0, 0, 1))
MA模型对偏自相关函数(PACF)拖尾,对自相关函数(ACF)截尾。在金融模型中,MA常用来刻画冲击效应,例如预期之外的事件。
ARMA模型
将AR和MA模型混合可得到ARMA模型,AR(p)和MA(q)共同组成了ARMA(p,q)。下面模拟一个ARMA(1,1)序列:
x <- arima.sim(n=1000, model=list(ar=0.5, ma=-0.5))
arima(x, order=c(1, 0, 1))
那么在建模过程中应该如何选择ARMA模型的最佳参数p和q呢?最常用的技术是采用循环在p和q各自0到5(或者更大)的范围内搜索最小AIC或BIC的(p,q)组合。
ARIMA模型
ARIMA模型是在ARMA模型的基础上解决非平稳序列的模型,因此在模型中会对原序列进行差分,下面模拟了一个ARIMA(1,1,1)模型:
x <- arima.sim(list(order = c(1,1,1), ar = 0.6, ma=-0.5), n = 1000
arima(x, order=c(1, 1, 1))
在ARIMA模型的基础上可以衍生出SARIMA模型,SRIMA模型能够刻画季节效应,如商品价格的周期性变动,在此不详细叙述。
By <- diff(y) # y_i - B y_i
B3y <- diff(y, 3) # y_i - B^3 y_i
message(paste0("y is: ", paste(y, collapse = ## y is: 1,3,5,10,20
## By is: 2,2,5,10
## B^3y is: 9,17自相关函数
要计算自相关,我们可以使用以下R函数:
get_autocor <- function(x, lag) {
x.left <- x[1:(length(x) - lag)]
x.right <- x[(1+lag):(length(x))]
autocor <- cor(x.left, x.right)
return(autocor)
}get_autocor(y, 1)
## [1] 0.9944627
# 相隔2个时间点(滞后期2)测量值的相关性
get_autocor(y, 2)
## [1] 0.9819805数据的高度自相关表明数据具有明确的时间趋势。
偏自相关
由于观察到较大滞后的自相关可以是较低滞后的相关结果,因此通常值得考虑偏自相关函数(pACF)。pACF的想法是计算偏相关性,这种相关性决定了对变量的最近观察样本的相关性。pACF定义为:
φkk:=Corr(yt,yt−k|yt−1,⋯,yt−k+1)k=0,1,2,⋯
使用pACF可以识别是否存在实际滞后的自相关或这些自相关是否是由其他样本引起的。
计算和绘制ACF和pACF的最简单方法是分别使用acf和pacf函数:
par(mfrow = c(1,2))
acf(y) # ACF
pacf(y) # pACF
在ACF可视化中,ACF或pACF被绘制为滞后的函数。指示的水平蓝色虚线表示自相关显着的水平。
分解时间序列数据
- St
- Tt
- ϵt
执行分解的方式取决于时间序列数据是加法还是乘法。
加法和乘法时间序列数据
加法模型假设数据可以分解为
yt = St + Tt + ϵt.
另一方面,乘法模型假设数据可以被分解为
- 添加:每个时期的季节效应放大相似。
- 乘法:季节性趋势随时间序列的变化而变化。
AirPassengers数据集提供了乘法时间序列的示例。
data(AirPassengers)
plot(AirPassengers)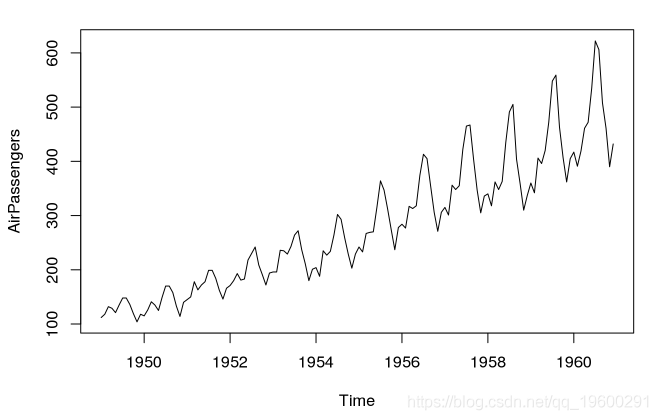
log(StTtϵt)=log(St)+log(Tt)+log(ϵt)
AirPassengers 数据集:
plot(log(AirPassengers))
正如我们所看到的,采用对数已经使季节性成分的幅度均衡。请注意,总体增长趋势没有改变。
在R中分解时间序列数据
要分解R中的时间序列数据,我们可以使用该decompose函数。请注意,我们应该通过type参数提供时间序列是加法的还是乘法的。
示例1:AirPassengers数据集
对于AirPassengers数据集,我们指定数据是乘法的并获得以下分解:
plot(decompose(AirPassengers, type = "multiplicative"))
分解表明,多年来航空公司乘客总数在增加。此外,我们已经观察到的季节性影响已被清楚地捕捉到。
示例2:EuStockMarkets数据集
让我们考虑可以EuStockMarkets数据集的分解:
daxData <- EuStockMarkets[, 1] #数据似乎不是可乘的,请使用加法分解
decomposed <- decompose(daxData, type = "additive")
plot(decomposed)
该图显示了1992年至1998年的DAX数据中的以下内容:
- 整体价格稳步上升。
- 季节性趋势强烈:每年年初,股价相对较低,并在夏季结束时达到相对最大值。
- 除1997年和1998年之间的最终测量外,随机噪声的贡献可以忽略不计。
平稳与非平稳过程
生成时间序列数据的过程可以是平稳的也可以是非平稳的。 例如,数据EuStockMarkets和AirPassengers数据都是非平稳的,因为数据有增加的趋势。为了更好地区分平稳和非平稳过程,请考虑以下示例:
par(mfrow = c(1,2)
library(tseries)
data(nino)
x <- nino3.4
plot(x, main = "Stationary process")# 飞机旅客数据
plot(AirPassengers, main = "Non-stationary process")
左图显示了一个平稳过程,其中数据在所有测量中表现相似。右图显示了一个非平稳过程,其中平均值随着时间的推移而增加。
介绍了与时间序列数据分析相关的最重要概念后,我们现在可以开始研究预测模型。
ARMA模型
ARMA代表自回归移动平均线。ARMA模型仅适用于平稳过程,并具有两个参数:
- p:自回归(AR)模型的阶数
- q:移动平均(MA)模型的阶数
使用backshift运算符制定ARMA模型
使用backshift运算符,我们可以通过以下方式制定ARMA模型:
ϕp(B)=1−∑pi=1ϕiBiϕp(B)=1−∑i=1pϕiBiθq(B)=1−∑qj=1θjBjθq(B)=1−∑j=1qθjBj
ϕp(B)yt=θq(B)ϵt.
ARIMA模型
总之,ARIMA模型具有以下三个参数:
- p:自回归(AR)模型的阶数
- d:差分阶数
- q:移动平均(MA)模型的阶数
在ARIMA模型中,通过将替换差分,将结果转换为差分yt
(1−B)dyt.
然后通过指定模型
ϕp(B)(1−B)dyt=θq(B)ϵt.
d=0(1−B)0yt=yt(1−B)0yt=ytdd
(1−B)1yt(1−B)2yt=yt−yt−1=(1−2B+B2)yt=yt−2yt−1+yt−2(1−B)1yt=yt−yt−1(1−B)2yt=(1−2B+B2)yt=yt−2yt−1+yt−2
在下文中,让我们考虑ARIMA模型的三个参数的解释。
p∈N0p∈N0d=0d=0Byt=yt−1Byt=yt−1ϕ1ϕ1yt−1yt−1yt−2yt−2ϕ1ϕ1ϕ2ϕ2
p=1 d=0 q=0
y^t=μϵt+ϕ1yt−1
自回归的影响
我们可以使用该arima.sim函数模拟自回归过程。通过该函数,可以通过提供要使用的MA和AR项的系数来指定模型。在下文中,我们将绘制自相关图,因为它最适合于发现自回归的影响。

第一个例子表明,对于ARIMA(1,0,0)过程,阶数1的pACF非常高,而对于ARIMA(2,0,0)过程,阶数1和阶数2自相关都很重要。因此,可以根据pACF显着的最大滞后来选择AR项的阶数。
ARIMA(0,1,0)模型简化为随机游走模型
y^t=μ+ϵt+yt−1.
差分的影响
以下示例演示了差分对AirPassengers数据集的影响:

虽然第一个图表显示数据显然是非平稳的,但第二个图表明差分时间序列是相当平稳的。
其中当前估计值取决于先前测量值的残差。
移动平均线的影响
可以通过绘制自回归函数来研究移动平均线的影响:
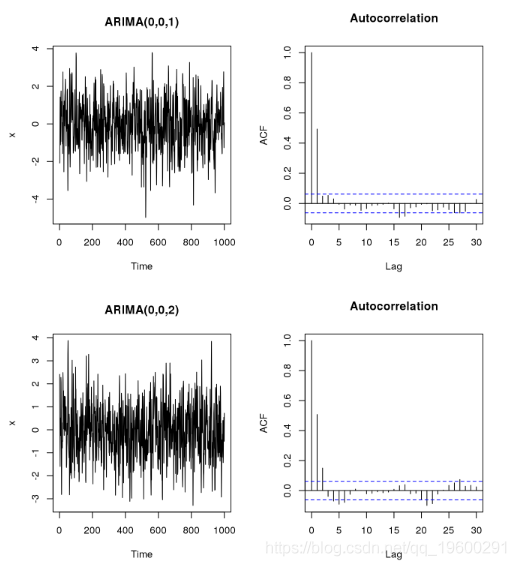
请注意,对于自回归图,我们需要注意第一个x轴位置表示滞后为0(即标识向量)。在第一个图中,只有第一个滞后的自相关是显着的,而第二个图表明前两个滞后的自相关是显着的。为了找到MA的阶数,适用与AR类似的规则:MA的阶数对应于自相关显着的最大滞后期。
在AR和MA之间进行选择
为了确定哪个更合适,AR或MA,我们需要考虑ACF(自相关函数)和PACF(偏ACF)。
AR和MA的影响
AR和MA的组合得到以下时间序列数据:

SARIMA模型
- P:季节性自回归(SAR)项的阶数
- D:季节差分阶数
- q:季节性移动平均线(SMA)的阶数
ARIMAX模型
R中的预测
auto.arimaforecast
SARIMA模型用于平稳过程
我们将使用数据展示ARMA的使用,该数据tseries给出了Nino Region 3.4指数的海面温度。让我们验证数据是否平稳:

d=0
为了验证是否存在任何季节性趋势,我们将分解数据:

没有整体趋势,这是平稳过程的典型趋势。但是,数据存在强烈的季节性因素。因此,我们肯定希望包含对季节性影响进行建模的参数。
季节性模型
(P,D,Q)S D=0
nino
S=12

P=2 Q=0
非季节性模型

我们可以使用包中的Arima函数来拟合模型forecast。
我们现在可以使用该模型来预测未来Nino 3.4地区的气温如何变化。有两种方法可以从预测模型中获得预测。第一种方法依赖于predict函数,而第二种方法使用包中的forecast函数。使用该predict功能,我们可以通过以下方式预测和可视化结果:
## ## Attaching package: 'ggplot2'## The following object is masked from 'package:forecast':## ## autolayer
如果我们不需要自定义绘图,我们可以使用以下forecast函数更轻松地获取预测和相应的可视化:
# 使用内置绘图功能:
forecast <- forecast(A, h = 60) # 预测未来5年
plot(forecast)用于非平稳数据的ARIMA模型
为了演示ARIMA模型对非平稳数据的使用,我们将使用数据集astsa。该数据集提供全球平均陆地 – 海洋温度偏差的年度测量值。
d=1



p=0q=1
我们现在可以预测未来几年平均陆地 – 海洋温度偏差将如何变化:

该模型表明,未来几年平均陆地 – 海洋温度偏差将进一步增加。
关于空气质量数据集的ARIMAX
为了展示ARIMAX模型的使用,我们将使用臭氧数据集 。
让我们加载臭氧数据集并将其划分为测试和训练集。请注意,我们已确保训练和测试数据包含连续的时间测量。
由于数据集未指示相对时间点,我们将手动创建此类注释:
为此,我们将在臭氧数据集中创建一个新列,该列反映了相对时间点:
现在我们有了时间维度,我们可以绘制臭氧水平的纵向行为:

时间序列数据似乎是平稳的。让我们考虑ACF和pACF图,看看我们应该考虑哪些AR和MA

自相关图非常不清楚,这表明数据中实际上没有时间趋势。因此,我们会选择ARIMA(0,0,0)模型。由于具有参数(0,0,0)的ARIMAX模型没有传统线性回归模型的优势,我们可以得出结论,臭氧数据的时间趋势不足以改善臭氧水平的预测。让我们验证一下:
print(Rsquared.linear)## [1] 0.7676977print(Rsquared.temporal)## [1] 0.7569718我们可以看到具有负二项式概率线性模型优于ARIMAX模型。
关于空气质量数据集的ARIMAX
要在更合适的数据集上演示ARIMAX模型,让我们加载数据集:
该Icecream数据集包含以下变量:
- 消费:冰淇淋消费量。
- 收入::美元平均每周家庭收入。
- 价格:每个冰淇淋的价格。
- temp:华氏温度的平均温度。
测量结果是从1951-03-18到1953-07-11的四周观测。
我们将模拟消费,冰淇淋消费作为时间序列,并使用收入,价格和平均值作为外生变量。在开始建模之前,我们将从数据框中创建一个时间序列对象。
我们现在调查数据:

因此,数据有两种趋势:
- 总体而言,1951年至1953年间,冰淇淋的消费量大幅增加。
- 冰淇淋销售在夏季达到顶峰。

由于季节性趋势,我们可能拟合ARIMA(1,0,0)(1,0,0)模型。但是,由于我们知道温度和外生变量的收入,因此它们可以解释数据的趋势:

income解释了整体趋势。此外,temp解释了季节性趋势,我们不需要季节性模型。因此,我们应该使用ARIMAX(1,0,0)模型进行预测。为了研究这些假设是否成立,我们将使用以下代码将ARIMAX(1,0,0)模型与ARIMA(1,0,0)(1,0,0)模型进行比较

ARIMAX(1,0,0)模型的预测显示为蓝色,而ARIMA(1,0,0)(1,0,0)模型的预测显示为虚线。实际观察值显示为黑线。结果表明,ARIMAX(1,0,0)明显比ARIMA(1,0,0)(1,0,0)模型更准确。
但请注意,ARIMAX模型在某种程度上不像纯ARIMA模型那样有用于预测。这是因为,ARIMAX模型需要对应该预测的任何新数据点进行外部预测。例如,对于冰淇淋数据集,我们没有超出1953-07-11的外生数据。因此,我们无法使用ARIMAX模型预测超出此时间点,而ARIMA模型可以实现:

如果您有任何疑问,请在下面发表评论。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据



