本文是我们通过时间序列和ARIMA模型预测拖拉机销售的制造案例研究示例。
第1部分 ：时间序列建模和预测简介
可下载资源
第2部分：在预测之前将时间序列分解为解密模式和趋势
第3部分：ARIMA预测模型简介
1 自回归模型AR
自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
自回归模型首先需要确定一个阶数p，表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为：
上式中yt是当前值,u是常数项,p是阶数 ri是自相关系数,et是误差。
自回归模型有很多的限制：
1、自回归模型是用自身的数据进行预测
2、时间序列数据必须具有平稳性
3、自回归只适用于预测与自身前期相关的现象
2 移动平均模型MA
移动平均模型关注的是自回归模型中的误差项的累加 ，q阶自回归过程的公式定义如下：
移动平均法能有效地消除预测中的随机波动。
3 自回归移动平均模型ARMA
自回归模型AR和移动平均模型MA模型相结合，我们就得到了自回归移动平均模型ARMA(p,q)，计算公式如下：
4 差分自回归移动平均模型ARIMA
将自回归模型、移动平均模型和差分法结合，我们就得到了差分自回归移动平均模型ARIMA(p,d,q)，其中d是需要对数据进行差分的阶数。
准备好开始分析，以预测未来3年的拖拉机销售情况。
步骤1：将拖拉机销售数据绘制为时间序列
首先，您已为数据准备了时间序列图。以下是您用于读取R中的数据并绘制时间序列图表的R代码。
data = ts(data[,2],start = c(2003,1),frequency = 12)
plot(data, xlab='Years', ylab = 'Tractor Sales')显然，上面的图表有拖拉机销售的上升趋势，还有一个季节性。
步骤2：差分数据使数据在平均值上保持不变（删除趋势）
用于绘制差异系列的R代码和输出显示如下：
plot(diff(data),ylab='Differenced Tractor Sales')
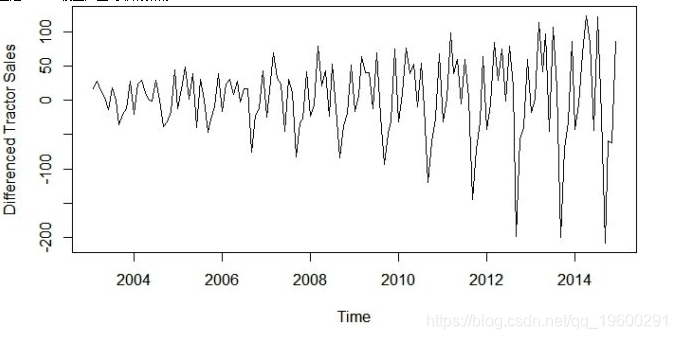
好的，所以上面的系列在方差上不是固定的，即随着我们向图表右侧移动，图中的变化也在增加。我们需要使系列在方差上保持稳定，以通过ARIMA模型产生可靠的预测。
步骤3：记录变换数据以使数据在方差上保持不变
使系列在方差上保持静止的最佳方法之一是通过对数变换转换原始系列。
以下是与输出图相同的R代码。请注意，由于我们在没有差分的情况下使用原始数据，因此该系列不是平均值。
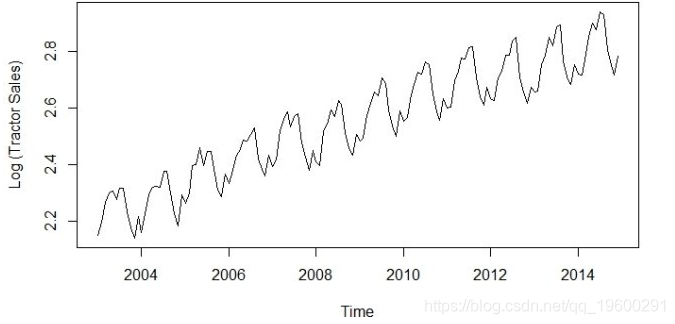
plot(log10(data),ylab='Log (Tractor Sales)')
现在方差上看起来很稳定。
步骤4： 差分对数变换数据使得数据在均值和方差上都是固定的
让我们看一下对数变换序列的差分图 。
plot(diff(log10(data)),ylab='Differenced Log (Tractor Sales)')
是的，现在这个系列在均值和方差上看起来都很稳定。
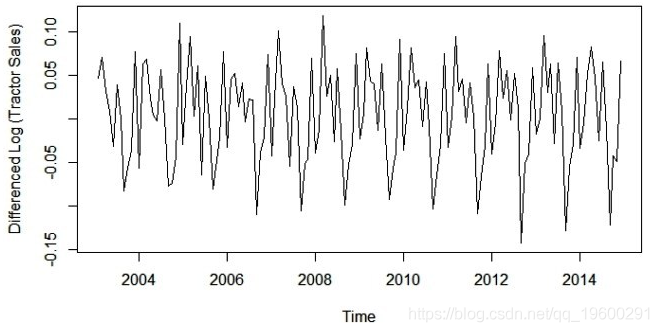
步骤5： 绘制ACF和PACF以识别潜在的AR和MA模型
现在，让我们创建自相关因子（ACF）和部分自相关因子（PACF）图来识别上述数据中的模式，这些模式在均值和方差上都是固定的。该想法是识别残差中AR和MA组分的存在。以下是生成ACF和PACF图的R代码。
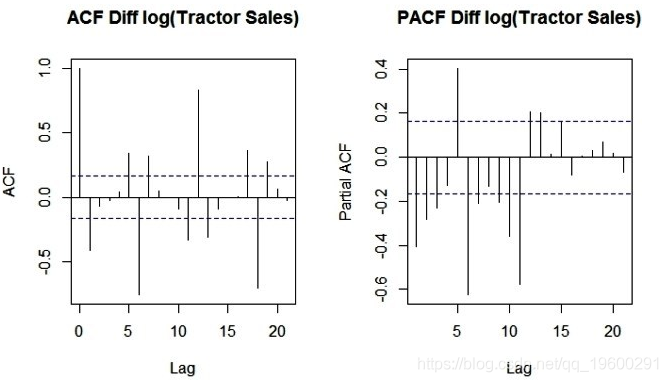
因为，在无效区域（虚线水平线）之外的图中有足够的尖峰，我们可以得出结论，残差不是随机的。这意味着AR和MA模型可以提取残差中的果汁或信息。此外，在滞后12处的残差中存在可用的季节性分量（由滞后12处的尖峰表示）。
这是有道理的，因为我们正在分析由于拖拉机销售模式而往往具有12个月季节性的月度数据。
步骤6： 确定最佳拟合ARIMA模型
R中的预测包中的自动动态功能有助于我们即时识别最适合的ARIMA模型。以下是相同的代码。请在执行此代码之前在R中安装所需的“预测”包。
ARIMAfit = auto.arima(log10(data), approximation=FALSE,trace=FALSE)
summary(ARIMAfit)随时关注您喜欢的主题
时间序列：log 10（拖拉机销售）最佳模型：ARIMA（0,1,1）（0,1,1）[12] MA1SMA1系数：-0.4047-0.5529SE0.08850.0734对数似然= 354.4AIC = -702.79AICC = -702.6BIC = -694.17
基于Akaike信息准则（AIC）和贝叶斯信息准则（BIC）值选择最佳拟合模型。我们的想法是选择具有最小AIC和BIC值的模型。我们将在下一篇文章中探讨有关AIC和BIC的更多信息。在R中开发的最佳拟合模型的AIC和BIC值显示在以下结果的底部：
正如预期的那样，我们的模型具有等于1的I（或积分）分量。这表示阶数1的差分。在上述最佳拟合模型中存在滞后12的附加差分。此外，最佳拟合模型具有1阶的MA值。此外，存在具有阶数1的滞后12的季节性MA。
步骤7：使用最合适的 ARIMA模型预测销售情况
下一步是通过上述模型预测未来3年（即2015年，2016年和2017年）的拖拉机销量。以下R代码为我们完成了这项工作。
par(mfrow = c(1,1))
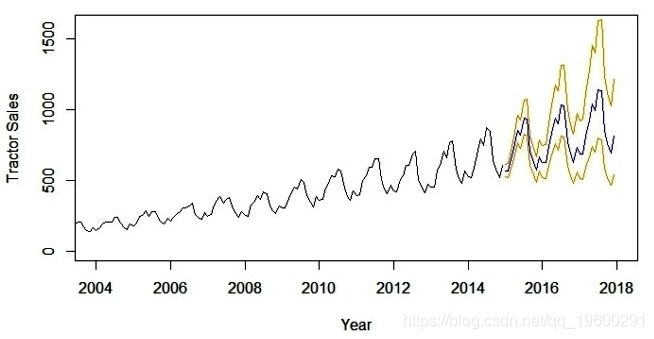
lines(10^(pred$pred-2*pred$se),col='orange')以下是拖拉机销售预测值为蓝色的输出。
此外，预测误差的范围（即标准偏差的2倍）在预测蓝线的两侧显示橙色线。
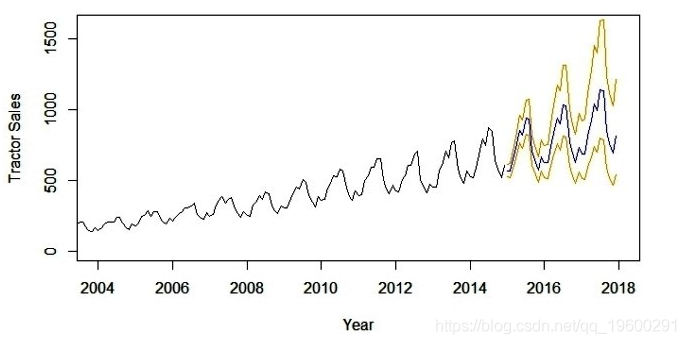
现在，长达3年的预测是一项挑战性的任务。这里的主要假设是时间序列中的下划线模式将继续保持与模型中预测的相同。短期预测模型，比如几个营业季度或一年，通常是一个合理准确的预测。像上述那样的长期模型需要定期评估（比如6个月）。我们的想法是将可用的新信息与模型中的时间推移相结合。
步骤8：为ACIM和PACF绘制ARIMA模型的残差
最后，让我们创建一个ACF和PACF的最佳拟合ARIMA模型残差的图，即ARIMA（0,1,1）（0,1,1）[12]。以下是相同的R代码。
pacf(ts(ARIMAfit$residuals),main='PACF Residual')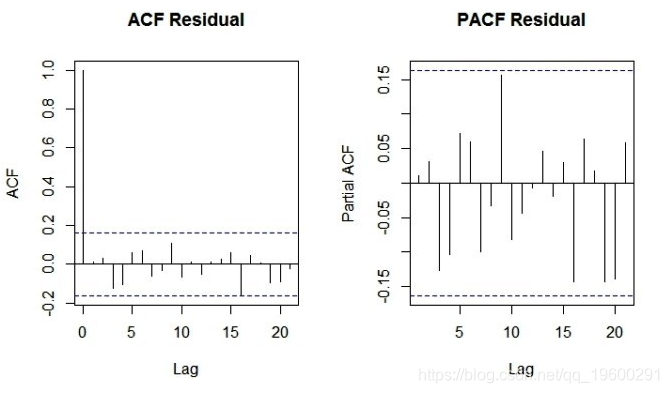
由于ACF和PACF图的无效区域之外没有尖峰，我们可以得出结论，残差是随机的。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
MATLAB图注意力网络GAT多标签图分类预测可视化
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
