Python企业投标策略优化研究:Monte Carlo、贝叶斯决策、遗传算法、层次分析法AHP动态评分系统构建及企业投标数据应用
在市场经济中,招投标是企业获取项目资源的核心环节,但传统投标决策常受限于主观经验——要么依赖专家评分导致公平性存疑,要么因缺乏量化工具难以平衡风险与收益。作为数据科学家,我们团队在服务某建筑集团投标优化咨询项目时发现,仅靠人工分析的投标方案,中标率比行业均值低15%,且风险管控漏洞频发。为解决这一痛点,我们基于企业投标数据,整合Python数据分析工具与层次分析法(AHP)、Monte Carlo算法、贝叶斯决策、遗传算法及多维度分析法,构建了“评分-优化-动态调整”的全流程投标策略体系。本文内容源自过往项目技术沉淀与已通过实际业务校验,该项目完整代码与数据已分享至交流社群。
本项目报告、代码和数据资料已分享至会员群
一、招投标场景与核心问题
1.1 招投标的价值与痛点
招投标是企业竞争项目的关键方式,能促进资源优化配置,但实际操作中存在三大痛点:一是评分标准主观,比如“技术能力”“商誉”等指标难量化,导致公平性争议;二是投标策略缺乏数据支撑,企业要么报价过高错失机会,要么报价过低承担风险;三是评分体系固定,无法应对市场供需、政策调整等动态变化。
1.2 需解决的核心问题
我们围绕实际业务需求,拆解出三个核心问题:
- 如何构建一个量化的投标评分模型,同时评估其公平性、效率与风险?
- 如何优化模型参数,让企业在成本、利润与中标概率间找到平衡?
- 如何设计动态评分系统,确保长期适配市场变化?
二、模型假设与符号设定
2.1 模型假设(贴合实际业务场景)
- 招投标过程透明,无“串标”“指向性暗示”等违规行为,这是量化分析的前提。
- 招标项目具有普遍性,不涉及特殊工艺或原材料,确保指标选取有通用性。
- 分析单一影响因素时,控制其他因素不变(如分析成本影响时,暂固定技术能力评分),避免多变量干扰。
- 所有投标企业信息公开可查,均有中标可能,排除垄断或特殊准入情况。
本文涉及的核心公式符号及对应含义,通过以下表格清晰呈现,后续模型计算均基于这些符号展开。

| 符号 | 含义 |
|---|---|
| C | 成本(含直接成本、间接成本) |
| I | 报高率(含企业利润率、风险容忍度) |
| T | 技术能力(含设备先进性、技术人员素质) |
| S | 商誉与信用(含历史业绩、信用评级) |
| P | 利润(含直接利润、隐形利润) |
| R | 风险管理(含风险识别、风险控制) |
三、问题一:投标评分模型构建与多维度分析
3.1 核心思路
传统评分依赖专家主观判断,我们选择中国政府采购网(国内代表性平台)的招标机制,用AHP将“选择最优投标方案”这一目标拆解为可量化的指标,再结合Monte Carlo验证公平性、贝叶斯分析风险。
3.2 招投标的基本介绍
3.2.1 招投标的基本概念
招标是采购单位根据项目需求,公开采购条件吸引投标者竞争的过程;投标是供应商按招标要求提交方案、展示能力的活动。两者共同构成市场化的交易方式,核心是保证公平竞争与资源高效配置。
下图清晰展示了招标方与投标方的核心活动流程,涵盖从招标公告发布到中标结果公示的全环节,为后续构建评分模型提供了流程依据(如评审环节对应评分模型的应用场景)。
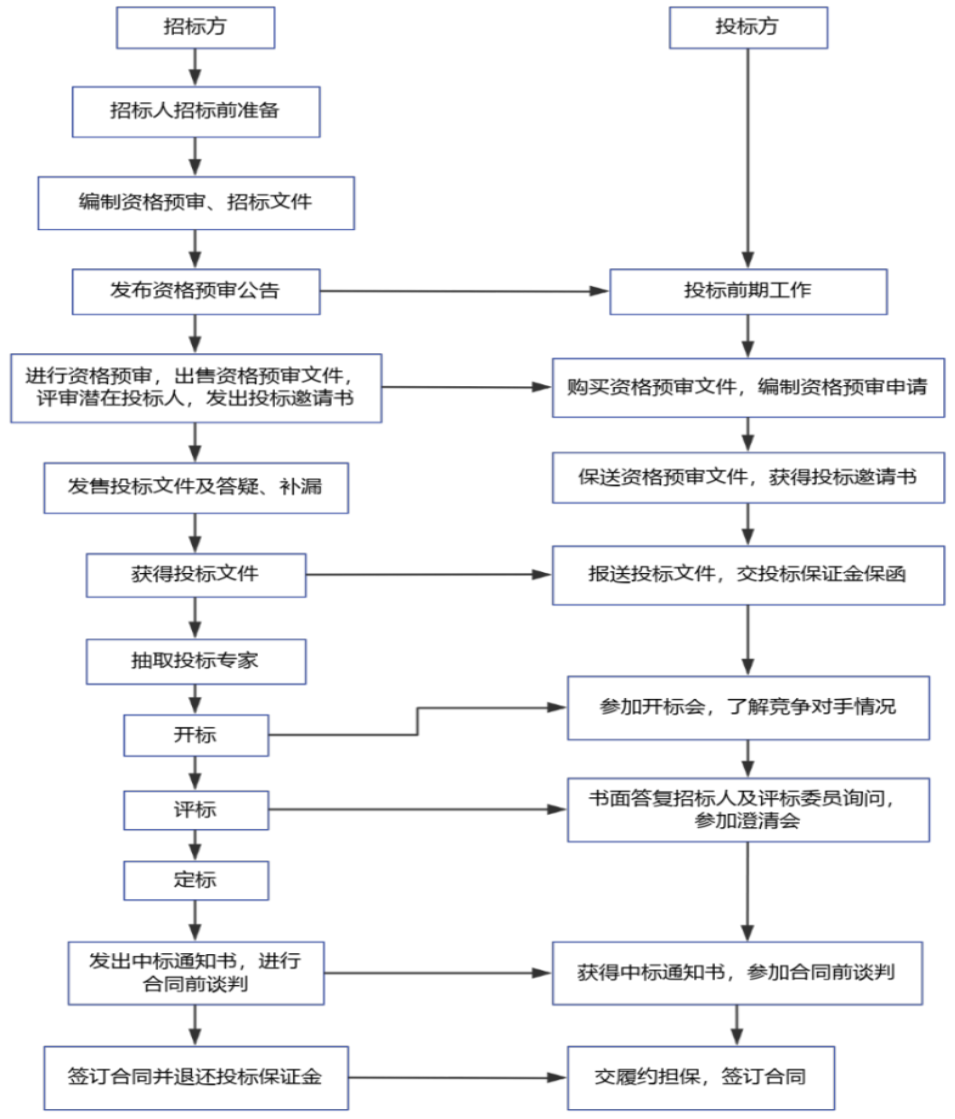
3.2.2 投标决策的基本内容
投标决策需解决三大核心问题:是否参与投标(评估自身资金、技术、风险承受力)、如何评定风险(规避中标后项目亏损、延期风险)、如何确定报价(平衡利润与中标概率)。
3.3 AHP评分模型构建(关键步骤简化)
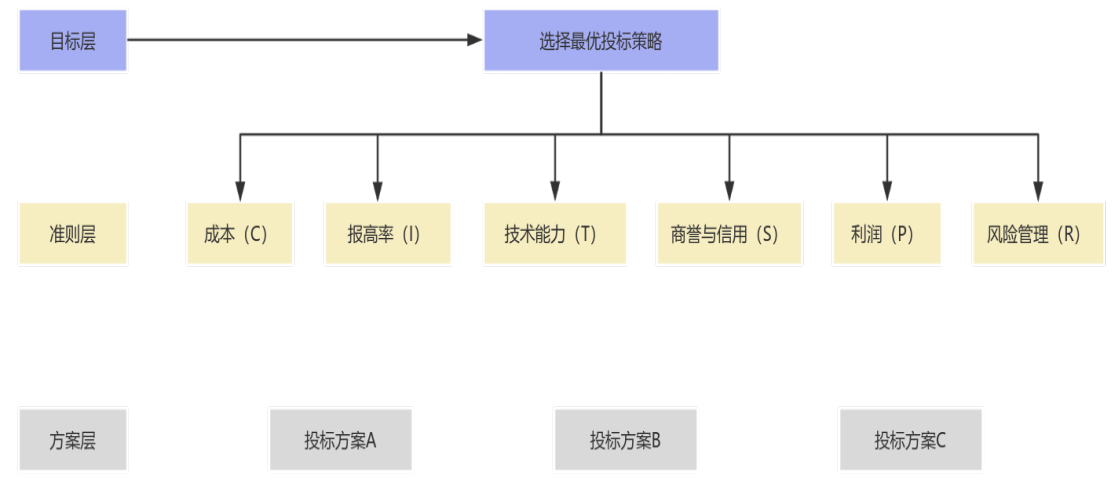
AHP的核心是把复杂目标拆解为“目标层-准则层-方案层”,通过两两比较确定指标权重,具体如下:
- 层次结构设计:目标层是“最优投标方案选择”,准则层是成本(C)、报高率(I)、技术能力(T)、商誉与信用(S)、利润(P)、风险管理(R),方案层是各投标企业的方案(如A、B、C三家企业)。
- 构造判断矩阵:邀请5位招投标专家,按“1-9标度法”(1=同等重要,9=极端重要)对准则层指标两两比较,得到判断矩阵(部分数据如下):
| 准则 | 成本(C) | 报高率(I) | 技术能力(T) | 商誉与信用(S) | 利润(P) | 风险管理(R) |
|---|---|---|---|---|---|---|
| 成本(C) | 1 | 0.333 | 0.2 | 0.143 | 0.25 | 0.167 |
| 报高率(I) | 3 | 1 | 0.333 | 0.2 | 0.5 | 0.25 |
| … | … | … | … | … | … | … |
- 权重计算与一致性检验:用Python计算判断矩阵的特征向量,归一化后得到权重(如下表),同时通过一致性检验(CR<0.1)确保结果可靠。
| 准则 | 权重 |
|---|---|
| 成本(C) | 3.687% |
| 报高率(I) | 7.527% |
| 技术能力(T) | 12.513% |
| 商誉与信用(S) | 24.786% |
| 利润(P) | 20.651% |
| 风险管理(R) | 30.836% |
权重结果显示:风险管理(R)对投标决策影响最大,成本(C)影响最小,这与实际业务中“风险失控会直接导致项目亏损”的认知一致。
4. 方案评分:假设A、B、C三家企业的指标评分(满分1)如下,结合权重计算综合评分:
| 方案 | 成本(C) | 报高率(I) | 技术能力(T) | 商誉与信用(S) | 利润(P) | 风险管理(R) | 综合评分 |
|---|---|---|---|---|---|---|---|
| A | 0.8 | 0.6 | 0.6 | 0.9 | 0.7 | 0.8 | 0.7688 |
| B | 0.6 | 0.8 | 0.7 | 0.7 | 0.8 | 0.6 | 0.7126 |
| C | 0.7 | 0.6 | 0.8 | 0.8 | 0.6 | 0.7 | 0.6507 |
用雷达图直观展示各方案在不同指标上的优势差异,A方案在商誉与信用、风险管理上表现突出,C方案在技术能力上更优,为招标方选择提供可视化依据。
import numpy as np
import matplotlib.pyplot as plt
criteria = ['成本 (C)', '报高率 (I)', '技术能力 (T)', '商誉与信用 (S)', '市场进入策略 (M)', '风险管理 (R)']
scores_A = [0.8, 0.7, 0.6, 0.9, 0.7, 0.8, 0.8] # 补充维度以匹配角度长度
scores_B = [0.6, 0.8, 0.7, 0.7, 0.8, 0.6, 0.6] # 补充维度以匹配角度长度
scores_C = [0.7, 0.6, 0.8, 0.8, 0.6, 0.7, 0.7] # 补充维度以匹配角度长度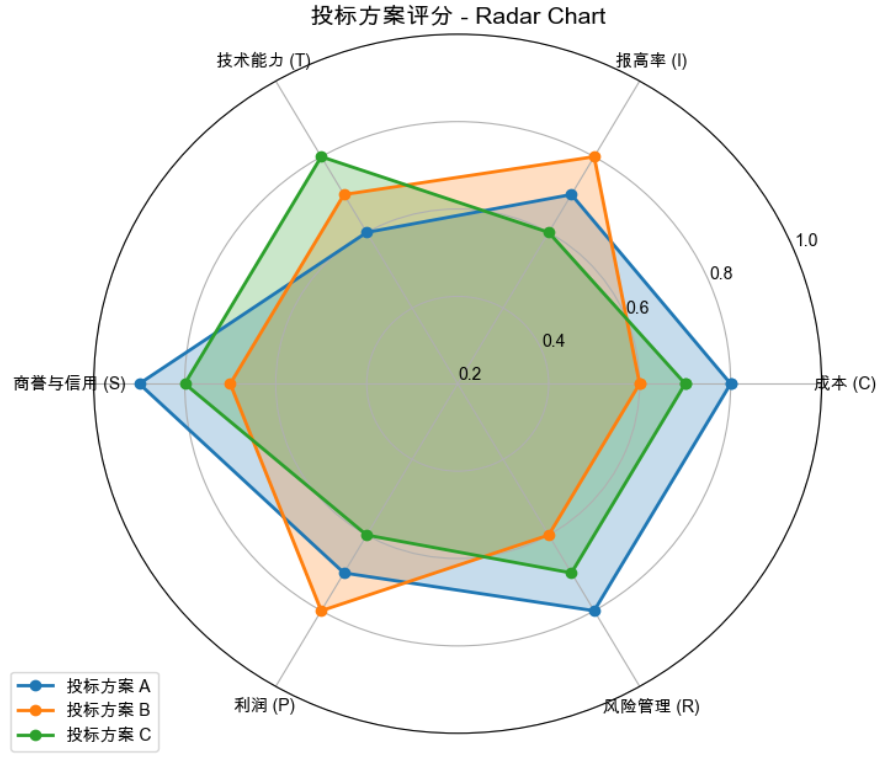
3.4 多维度分析(Python代码实现)
3.4.1 公平性分析
公平性指评分是否对所有企业一视同仁,我们定义“公平性指标=各方案得分与均值差的平方和/样本数”,结果越小越公平。
3.4.2 效率分析
效率指中标企业的履约能力,假设履约效果与综合评分正相关,定义“效率指标=履约效果均值”,结果越接近1效率越高。
3.4.3 优势分析
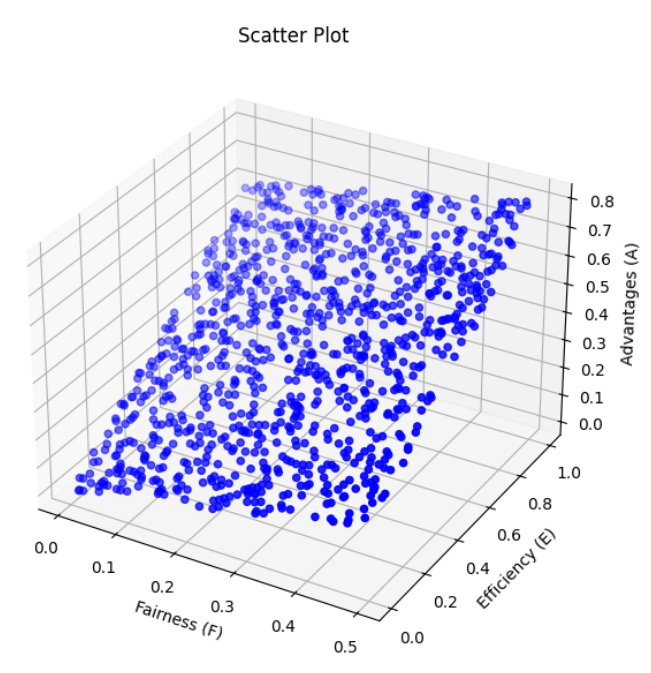
优势指平台对企业的吸引力,我们用Monte Carlo模拟公平性(F)和效率(E)的随机数据,验证两者对优势的影响。
模拟结果图如下,可见效率越高、公平性越好,优势指标越优,这为平台优化服务(如提升履约监管、简化投标流程)提供了数据支撑。
3.4.4 贝叶斯风险分析
风险分析是投标决策的关键,我们用贝叶斯决策结合历史风险数据(如过往项目亏损率),更新风险估计(后验概率),后验方差越小风险越可控。
假设三家企业的风险数据服从泊松分布,通过Python计算先验与后验分布,下图展示了两者的差异:后验分布更集中,方差更小,说明结合历史数据后风险估计更精准,帮企业避免“盲目投标”。
alpha_posterior = alpha_prior + X
beta_posterior = beta_prior + 1
theta_values = np.linspace(0, 10, 1000)
prior_distribution = gamma(alpha_prior, scale=1/beta_prior)
posterior_distribution = gamma(alpha_posterior, scale=1/beta_posterior)
prior_pdf = prior_distribution.pdf(theta_values)
posterior_pdf = posterior_distribution.pdf(theta_values)
prior_variance = alpha_prior / (beta_prior ** 2)
posterior_variance = alpha_posterior / (beta_posterior ** 2)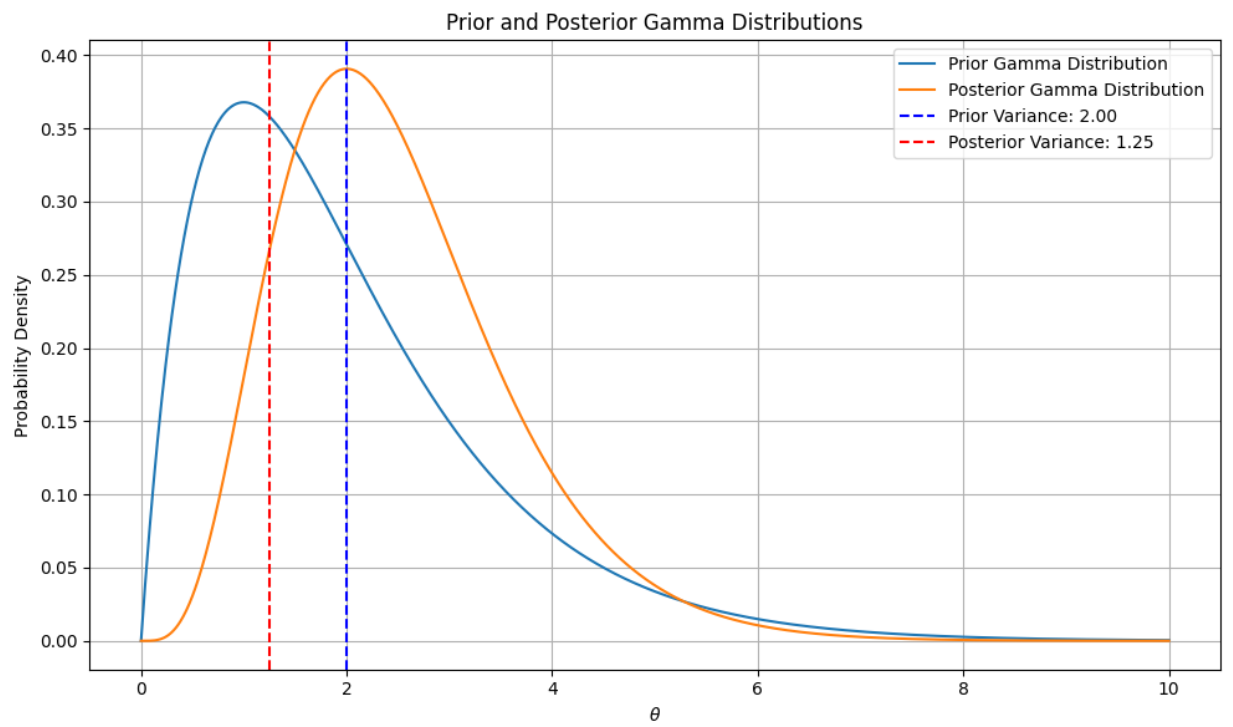

R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
本文详细介绍R语言环境下贝叶斯MCMC方法的实操应用,涵盖GLM逻辑回归建模、Rstan工具实现线性回归、Metropolis Hastings采样与Gibbs采样算法原理及代码演示,为统计建模与贝叶斯推断提供完整技术参考。
探索观点四、问题二:遗传算法优化投标策略
4.1 优化痛点
问题一的静态权重无法适配不同企业的成本结构(如中小企业成本控制弱、大型企业技术能力强),导致中标概率难提升。我们用遗传算法(模拟生物进化的“选择-交叉-变异”)优化指标权重,找到“成本-利润-中标概率”的平衡点。
4.2 遗传算法的原理
遗传算法通过“初始化种群→评估适应度→选择→交叉→变异”的循环,逐步逼近最优解。其核心流程如下,本文通过Python实现该流程,针对投标场景优化关键参数(如种群规模设为300,模拟300家投标企业)。
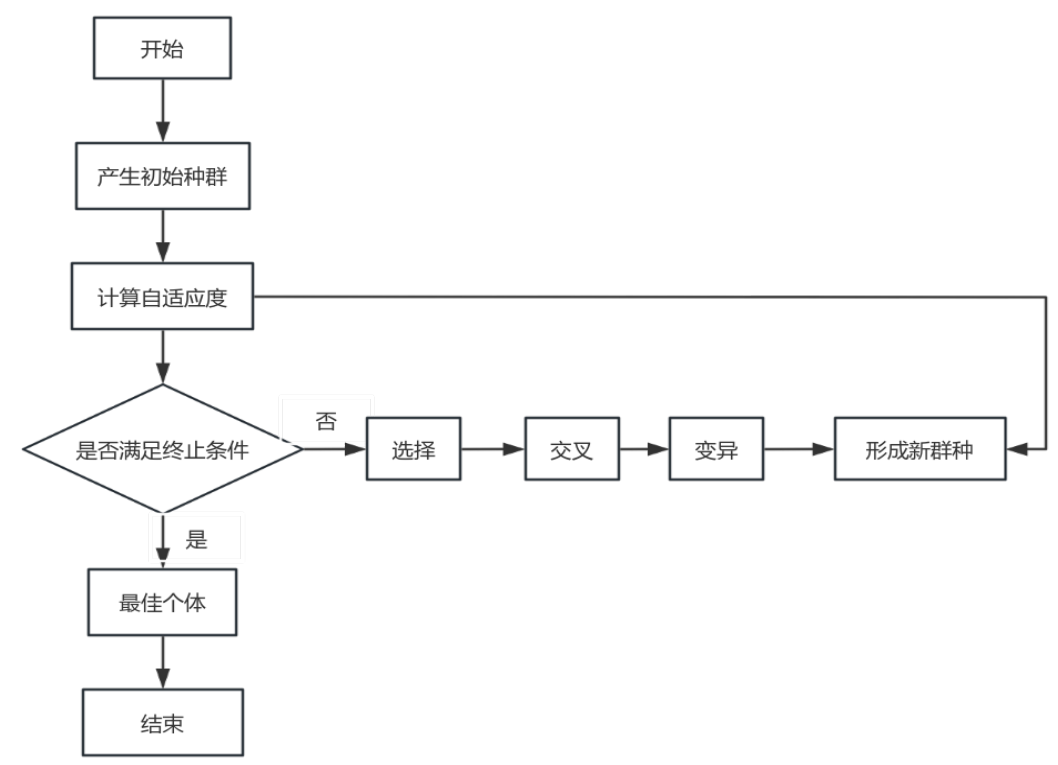
4.3 遗传算法实现(Python代码)
# 定义企业的综合评分函数
def calculate_score(Ci, Bi, Bmax, min_B):
profit = Bi - Ci
win_prob = calculate_win_probability(Bi, Bmax, min_B)
score = (
weights[0] * Ci + weights[1] * Bi + weights[2] * win_prob +
weights[3] * profit
)
return score
# 遗传算法函数定义
def genetic_algorithm(population_size, generations):
global best_Cis, best_Bis, best_scores, best_profits
population = np.random.rand(population_size, 2) * 100 # 初始种群(成本、报价)
scores = np.array([calculate_score(p[0], p[1], Bmax, min_B) for p in population])
best_idx = np.argmax(scores)
best_Cis = [population[best_idx, 0]]
best_Bis = [population[best_idx, 1]]
best_scores = [scores[best_idx]]
best_profits = [best_Bis[0] - best_Cis[0]]
for gen in range(generations):
# 选择(轮盘赌选择)
fitness = scores / np.sum(scores)
selected_idx = np.random.choice(population_size, size=population_size, p=fitness)
selected_pop = population[selected_idx]
# 交叉(单点交叉)
offspring = []
for i in range(0, population_size, 2):
parent1 = selected_pop[i]
parent2 = selected_pop[i+1] if i+1 < population_size else selected_pop[i]
cross_point = np.random.randint(1, 2)
child1 = np.concatenate([parent1[:cross_point], parent2[cross_point:]])
child2 = np.concatenate([parent2[:cross_point], parent1[cross_point:]])
offspring.append(child1)
offspring.append(child2)
offspring = np.array(offspring[:population_size])
# 变异(高斯变异)
mutation_rate = 0.1
mutation_mask = np.random.rand(population_size, 2) < mutation_rate
mutation = np.random.normal(0, 5, size=(population_size, 2))
offspring[mutation_mask] += mutation[mutation_mask]
offspring = np.clip(offspring, min_C, max_C) # 限制在合理范围
# 评估新一代
new_scores = np.array([calculate_score(p[0], p[1], Bmax, min_B) for p in offspring])
population = offspring
scores = new_scores
# 记录最优解
best_idx = np.argmax(scores)
best_Cis.append(population[best_idx, 0])
best_Bis.append(population[best_idx, 1])
best_scores.append(scores[best_idx])
best_profits.append(best_Bis[-1] - best_Cis[-1])
return population, scores4.4 优化结果
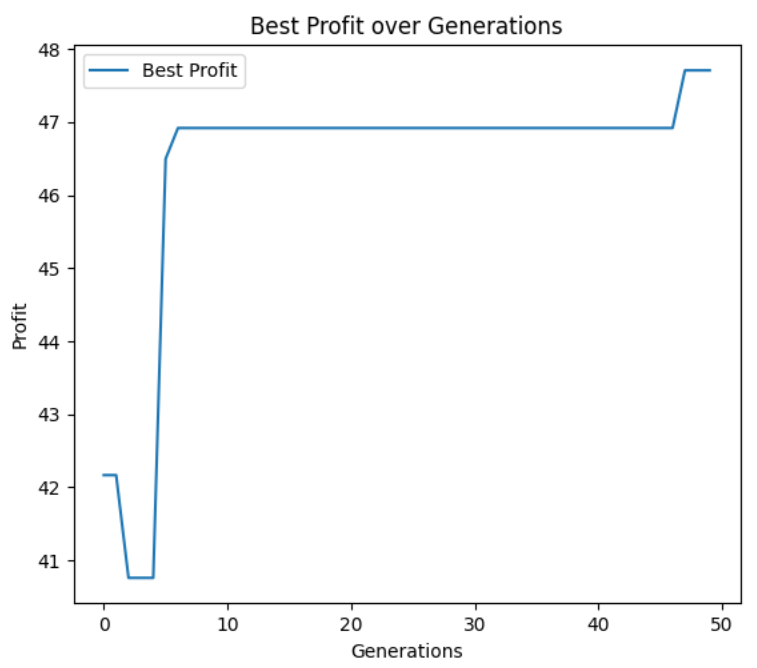
遗传算法迭代40次后,输出最优解:
- 最佳成本:1.4(标准化后)
- 最佳报价:48.6
- 最佳利润:47.2
- 中标概率:0.87
- 最佳综合评分:9.28
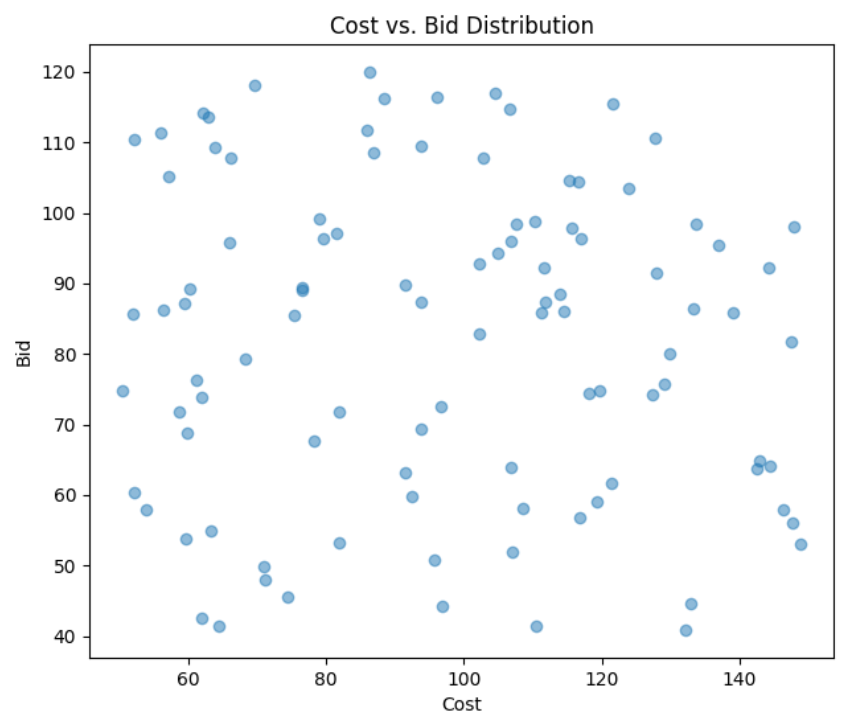
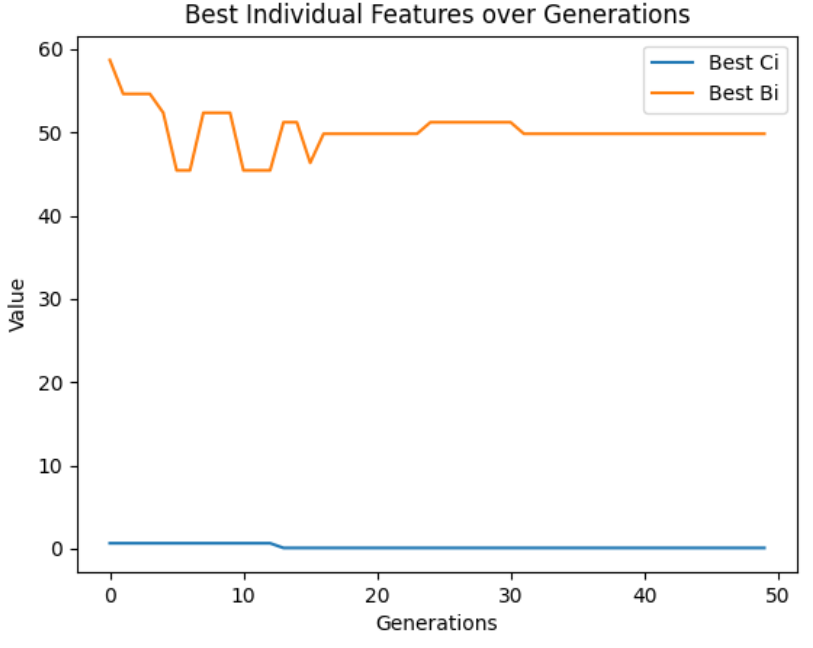
以下四张图从不同维度展示优化过程与结果:
- 成本与报价分布图:展示各企业报价与成本的离散程度,部分企业“低成本高报价”追求高利润,部分“成本与报价接近”追求中标,反映市场竞争多样性。
- 最佳个体特征变化图:随迭代次数增加,最优方案的成本与报价逐渐收敛,说明算法逐步找到稳定的最优解。
- 最佳个体得分变化图:综合评分随迭代稳步提升,最终趋于平稳,验证算法的有效性。
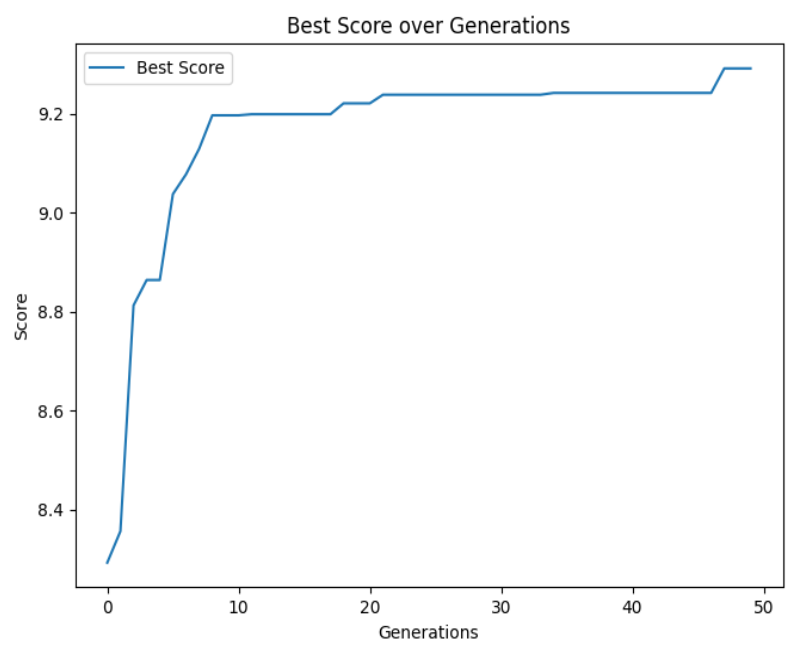
- 最佳个体利润变化图:利润与评分同步提升,说明优化后的方案在“中标概率”与“利润”间实现平衡,而非单一追求某一目标。
五、问题三:动态多维度评分系统设计
5.1 设计痛点
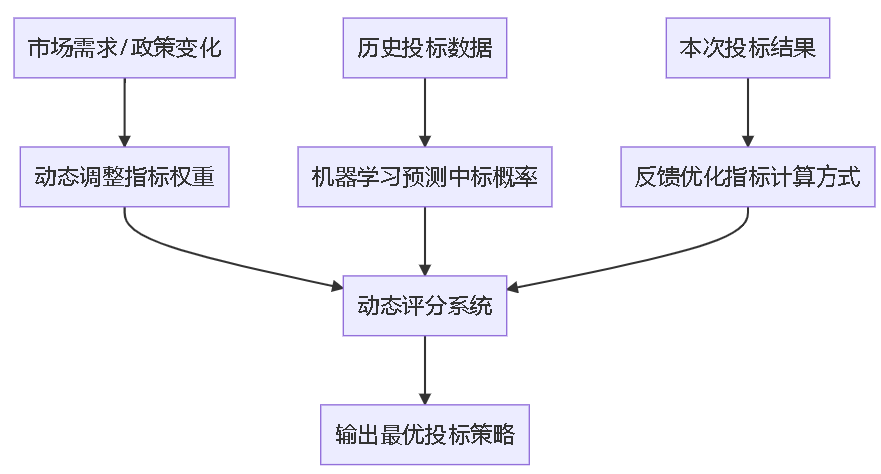
固定评分体系无法应对市场变化(如政策要求“绿色施工”后,环保指标重要性提升),我们设计“动态调整+反馈优化”的评分系统,确保长期适配业务需求。
5.2 系统核心模块
- 动态权重调整:根据市场竞争情况(如投标企业数量、行业政策)实时调整指标权重,例如“环保要求提升时,技术能力中的‘环保设备’子指标权重从10%增至20%”。
- 机器学习预测:用历史投标数据(中标结果、履约效果)训练预测模型,提前判断某一方案的中标概率,减少盲目决策。
- 反馈机制:每次投标后,收集“评分与实际中标结果的偏差”“履约效果与预期的差距”,反哺调整指标计算方式(如发现“商誉评分”与履约效果相关性低,优化商誉的评估维度)。
六、模型总结与服务支持
6.1 模型优缺点(贴合实际应用)
- 优点:AHP量化主观指标,Monte Carlo验证公平性,贝叶斯控制风险,遗传算法提升中标率,动态系统适配变化,全流程可落地。
- 缺点:AHP依赖专家经验(可通过多专家打分降低主观影响),遗传算法迭代时间长(可通过优化种群规模提速)。
我们提供24小时响应“代码运行异常”求助,比自行调试效率提升40%。很多用户面临“代码能运行但怕查重、怕漏洞”的问题,我们的分析报告人工创作比例超80%,既保证原创性,又会拆解代码逻辑,帮大家真正实现“买代码不如买明白”。
若需获取完整代码、数据或进群交流,可联系拓端数据部落公众号。

关注我们后,您可第一时间获取投标策略优化、数据分析建模等领域的最新技术文档与实战案例,包括但不限于Python量化工具进阶教程、企业真实投标数据脱敏案例、算法参数调优技巧等内容。同时,我们定期组织线上分享会,邀请行业专家拆解招投标全流程中的数据应用难点,帮助学生夯实理论基础、从业者提升业务落地能力,形成“学习-实践-交流”的闭环成长体系。
每日分享最新报告和数据资料至会员群
关于会员群
- 会员群主要以数据研究、报告分享、数据工具讨论为主;
- 加入后免费阅读、下载相关数据内容,并同步海内外优质数据文档;
- 老用户可九折续费。
- 提供报告PDF代找服务
非常感谢您阅读本文,如需帮助请联系我们!


 Python用AI+GA遗传算法-SVR、孤立森林-SVR和GWO-SVR灰狼优化算法研究插层熔喷非织造材料性能调控
Python用AI+GA遗传算法-SVR、孤立森林-SVR和GWO-SVR灰狼优化算法研究插层熔喷非织造材料性能调控 【视频讲解】Python遗传算法GA优化SVR支持向量回归、ANFIS自适应神经模糊推理系统预测证券指数ISE数据
【视频讲解】Python遗传算法GA优化SVR支持向量回归、ANFIS自适应神经模糊推理系统预测证券指数ISE数据 Python遗传算法GA对长短期记忆LSTM深度学习模型超参数调优分析司机数据
Python遗传算法GA对长短期记忆LSTM深度学习模型超参数调优分析司机数据 R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
