作为数据科学家,日常工作里常与各类数据和算法打交道,致力于从繁杂数据中挖掘价值、解决实际业务难题。
在项目中,面对业务场景数据的分类需求,传统朴素贝叶斯方法在处理非正态分布数据时的局限逐渐凸显,促使我们探索创新的解决方案,也就是核密度估计朴素贝叶斯(Kernel Density Estimation Naive Bayes,KDE – Naive Bayes)方法 。
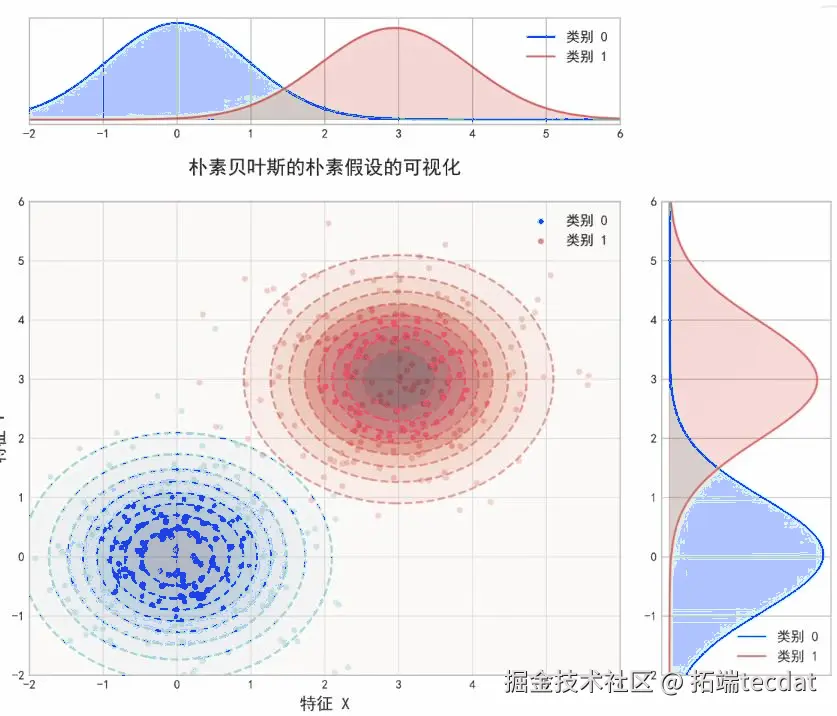
在实际业务里,数据形态多样,传统朴素贝叶斯依赖预设分布(如高斯分布),遇到非正态数据易拟合失真,影响分类准确性,进而给业务决策带来偏差。而核密度估计朴素贝叶斯,无需预先设定似然函数,还能通过多重核密度估计计算特征联合分布,突破“朴素”假设限制。这一方法在项目实践中展现出良好效果,为解决类似业务数据分类问题提供了新路径。
为让大家更好交流学习,专题项目文件已分享在交流社群,阅读原文进群和500 + 行业人士共同交流和成长,一起在数据科学助力业务发展的道路上探索前行。
其中,( P(XC_k) ) 是似然函数,描述类别 ( C_k ) 下特征 ( X ) 的概率分布;( P(C_k) ) 是先验分布,代表类别 ( C_k ) 出现的先验概率;
( P(X) ) 是证据因子,为特征 ( X ) 出现的总概率 。
朴素贝叶斯有一关键“朴素假设”,即认为特征向量 ( X = (x_1, x_2, \cdots, x_n) ) 中各特征相互独立,于是:
以业务场景中的某类数据为例,数据分布并非标准正态,用传统朴素贝叶斯的高斯分布假设去拟合,得到的概率密度曲线与实际数据分布偏差明显,分类准确率(如项目中某业务分类任务,传统方法准确率仅 0.5585 )难以满足业务对精准分类、辅助决策的需求。这就像用标准模具去套形状各异的零件,很多时候无法契合,导致后续基于分类结果的业务策略制定可能出现偏差,影响业务推进和效果。
# 导入相关库,用于数据处理和核密度估计等操作
import numpy as np
from scipy.stats import gaussian_kde
# 假设 data 是业务场景数据,包含特征和类别标签,这里简单模拟数据加载和处理
# 实际业务中,data 需根据具体业务数据格式和来源进行读取、清洗等操作
data = np.random.randn(1000, 5) # 模拟数据,实际为业务场景数据
# 分离特征和标签,假设标签在最后一列
features = data[:, :-1]
labels = data[:, -1]
# 定义核密度估计朴素贝叶斯分类函数的核心部分
def kde_naive_bayes_classify(feature_sample, features, labels):
# 获取类别数量
unique_labels = np.unique(labels)
# 存储各类别概率
label_probs = []
for label in unique_labels:
# 筛选出对应类别的特征数据
class_features = features[labels == label]
# 对每个特征维度进行核密度估计
kde_models = [gaussian_kde(class_features[:, i]) for i in range(class_features.shape[1])]
# 计算该样本在各类别下的概率(似然部分)
prob = 1
for i in range(len(kde_models)):
prob *= kde_models[i].evaluate([feature_sample[i]])[0]
# 这里简单假设先验概率均等,实际业务中可根据数据统计得到
prior_prob = np.mean(labels == label)
label_probs.append(prob * prior_prob)
# 返回概率最大的类别
return unique_labels[np.argmax(label_probs)]
通过这样的代码逻辑,对业务场景数据进行分类。在项目的实际应用中,当设置带宽(bandwidth )为 ‘Scott’ 时,分类准确率提升到 0.826 ,相比传统朴素贝叶斯有显著改善。这意味着在业务决策中,基于该分类结果制定的策略,能更贴合实际数据规律,为业务带来更有效的支撑,比如在客户分类、业务风险识别等场景中,更精准的分类有助于企业针对性开展营销、风险管控等工作,提升业务效益。
核密度估计朴素贝叶斯的优劣势分析
优点
- 适配多样数据:无需预先设定似然函数,不管业务数据是何种复杂分布,都能通过核密度估计去适配,拓宽在不同业务场景的应用可能性。像处理电商交易数据中用户行为特征的复杂分布、金融数据中风险指标的特殊分布等,都能发挥作用 。
- 突破特征独立假设:借助多重核密度估计计算特征联合分布,能更真实反映业务数据中特征间的关联,让分类更精准。例如在分析企业运营数据时,多个运营指标(如营收、成本、用户活跃度等 )相互影响,该方法可更好捕捉这种关系,辅助企业精准分类运营状态 。
缺点
- 计算成本较高:由于要对每个特征维度进行核密度估计,且核密度估计本身计算复杂,当业务数据量庞大、特征维度较多时,计算量会显著增加,可能影响业务应用中的处理效率。比如在处理大规模互联网用户行为数据时,若特征维度达数十个,计算时间会明显拉长,对实时性要求高的业务场景(如实时推荐、实时风险预警 )带来挑战 。
- 带宽设置敏感:需要设定合适的 bandwidth 值,值过低可能导致过拟合,使模型在训练数据上表现好,但对实际业务中的新数据分类效果差;值过高又可能欠拟合,丢失数据细节。在业务实践中,需通过多次试验、结合业务效果评估来找到合适的带宽设置,增加了应用的复杂度和试错成本 。
关于分析师
Xing Gao
在此对 Xing Gao 对本文所作的贡献表示诚挚感谢,他在温州大学完成了应用心理学专业的学习,曾担任心理老师。擅长 Python、SPSS、Mplus、Amos、Excel、SQL、Tableau,在随机对照试验、问卷研究、心理测评、数据分析、机器学习方面有相关能力 。涵盖随机对照试验、问卷研究、心理测评等领域。他在数据分析、机器学习等方面拥有专业知识,并具备使用多种数据处理与分析工具的优势,能够胜任相关的研究与实践工作。

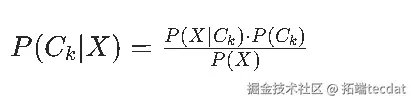
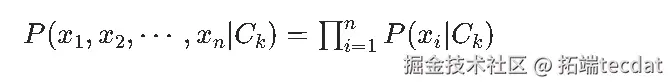
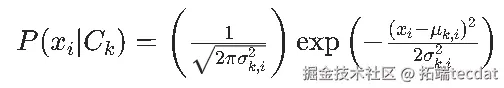

 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据
Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据 MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
