最近我们被客户要求撰写关于用ARIMA模型进行预测的研究报告。
考虑一些简单的平稳的AR(1)模拟时间序列。
> for(t in 2:n) X\[t\]=phi*X\[t-1\]+E\[t\] > plot(X,type="l")
可下载资源
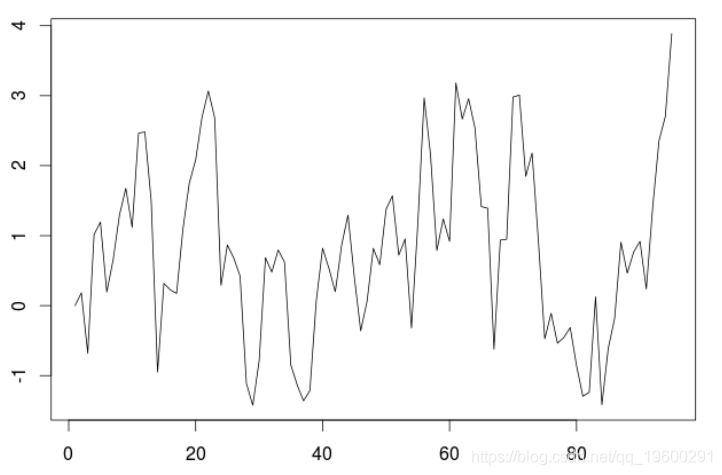
如果我们拟合一个AR(1)模型。
如果一个时间序列经过平稳性检验后得到是一个平稳非白噪声序列,那么该序列中就蕴含着相关性的信息。
在统计学中,通常是建立一个线性模型来拟合该时间序列的趋势。其中,AR、MA、ARMA以及ARIMA都是较为常见的模型。
1、AR(Auto Regressive Model)自回归模型
AR是线性时间序列分析模型中最简单的模型。通过自身前面部分的数据与后面部分的数据之间的相关关系(自相关)来建立回归方程,从而可以进行预测或者分析。下图中展示了一个时间如果可以表示成如下结构,那么就说明它服从p阶的自回归过程,表示为AR(p)。其中,ut表示白噪声,是时间序列中的数值的随机波动,但是这些波动会相互抵消,最终是0。theta表示自回归系数。
所以当只有一个时间记录点时,称为一阶自回归过程,即AR(1)。
2、MA(Moving Average Model)移动平均模型
通过将一段时间序列中白噪声序列进行加权和,可以得到移动平均方程。如下图所示为q阶移动平均过程,表示为MA(q)。theta表示移动回归系数。ut表示不同时间点的白噪声。
3、ARMA(Auto Regressive and Moving Average Model)自回归移动平均模型
自回归移动平均模型是与自回归和移动平均模型两部分组成。所以可以表示为ARMA(p, q)。p是自回归阶数,q是移动平均阶数。
从式子中就可以看出,自回归模型结合了两个模型的特点,其中,AR可以解决当前数据与后期数据之间的关系,MA则可以解决随机变动也就是噪声的问题。
4、ARIMA(Auto Regressive Integrate Moving Average Model)差分自回归移动平均模型
同前面的三种模型,ARIMA模型也是基于平稳的时间序列的或者差分化后是稳定的,另外前面的几种模型都可以看作ARIMA的某种特殊形式。表示为ARIMA(p, d, q)。p为自回归阶数,q为移动平均阶数,d为时间成为平稳时所做的差分次数,也就是Integrate单词的在这里的意思。
具体步骤如下:
-
获取被观测系统时间序列数据;
-
对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
-
经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q
-
由以上得到的d、q、p,得到ARIMA模型。然后开始对得到的模型进行模型检验。
arima(X,order=c(1,0,0), + include.mean = FALSE)
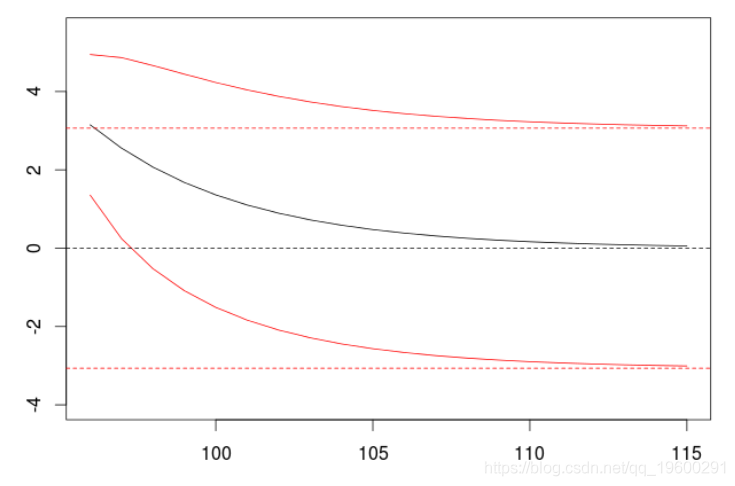
我们观察到预测值向0的指数衰减,以及增加的置信区间(其中方差增加,从白噪声的方差到平稳时间序列的方差)。普通线是有条件的预测(因为AR(1)是一个一阶马尔可夫过程),虚线是无条件的。让我们存储一些数值,把它们作为基准。
如果我们拟合一个MA(1)模型
> P=predict(model,n.ahead=20) > plot(P$pred)
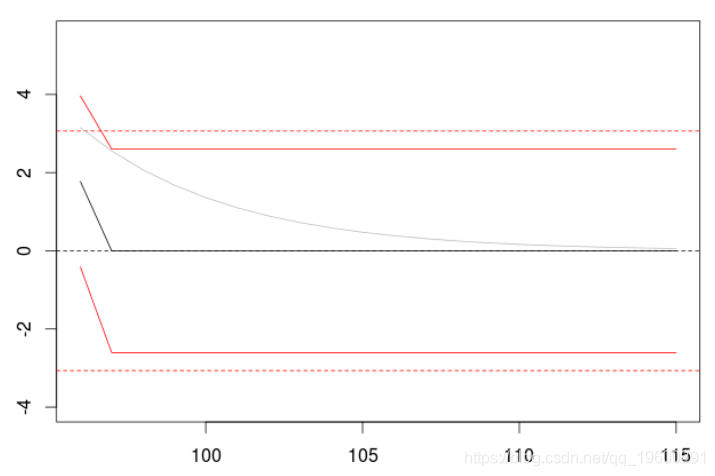
在两个滞后期之后,预测是无效的,而且(条件)方差保持不变。但如果我们考虑一个具有较长阶数的移动平均过程。
> P=predict(model,n.ahead=20) > plot(P$pred) >
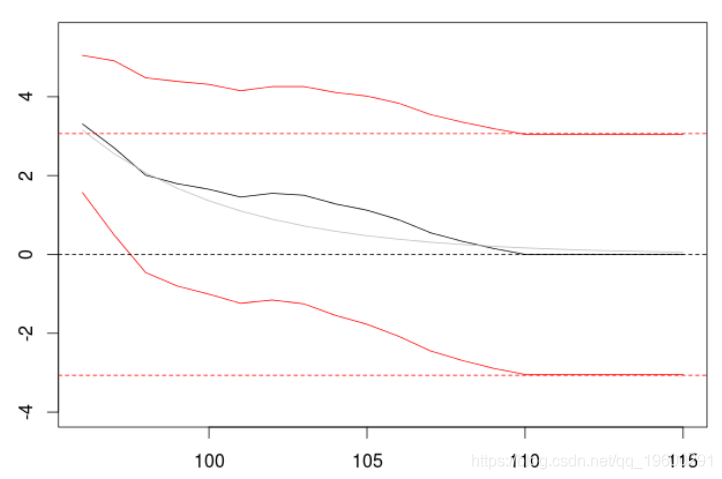
我们得到一个可以与AR(1)过程相比较的输出。因为我们的AR(1)过程也可以被看作是一个具有无限阶数的MA(∞)。
但是,如果我们认为时间序列不是平稳的,那么我们就拟合一个arima模型
> model=arima(X,order=c(0,1,0), + include.mean = FALSE)
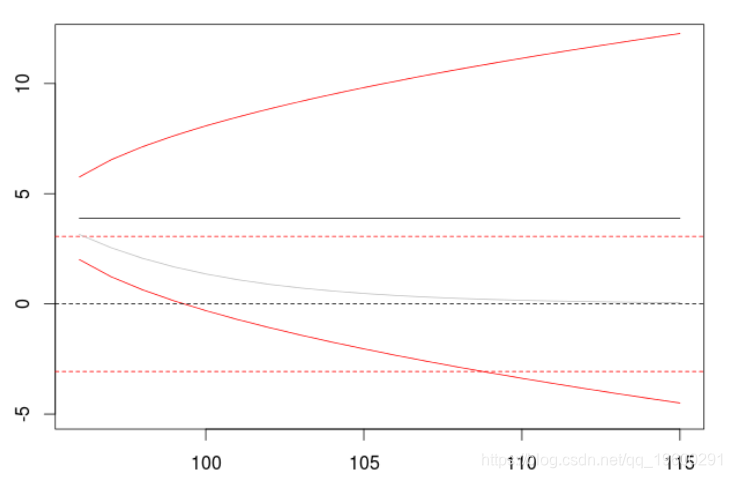
我们观察到:预测是平稳的,置信区间不断增加,实际上,方差向无穷大增加(以线性速度)。因此,在区分一个时间序列时应该非常小心,它将对预测产生巨大影响。


 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略
Python中国证券成分股波动率量化:ARIMA-随机森林预测、MPT投资组合优化、四维评价体系与动态仓位策略 Python基于ARIMA-LSTM模型的广州市新能源汽车销量预测
Python基于ARIMA-LSTM模型的广州市新能源汽车销量预测



